Gleichmäßig beschleunigte Bewegung

Untersuchung einer nicht gleichförmigen Bewegung

Nun wollen wir eine nicht gleichförmige Bewegung untersuchen. Dazu verwenden wir erneut die Luftkissenbahn und erhöhen diese auf einer Seite, so dass der Wagen eine schiefe Ebene hinunterfährt.

Der Wagen wird am Startpunkt losgelassen, und es werden erneut die Zeiten für die zurückgelegten Streckenabschnitte gemessen und in eine Tabelle eingetragen.

Beobachtung:

Der Wagen wird kontinuierlich schneller – es handelt sich also um eine beschleunigte Bewegung.

Messwerte:

s in cm	t in s	$\dfrac {\Delta s}{\Delta t}$ in $\dfrac {cm}{s}$
0	0	–
20	1,11	18,0
40	1,57	43,5
60	1,96	51,3
80	2,25	69,0
100	2,50	80,0
120	2,73	87,0

Grafische Auswertung:

Wir zeichnen wie beim vorherigen Versuch ein Diagramm, indem die zurückgelegte Wegstrecke in Abhängigkeit der benötigten Zeit aufgetragen wird.

Zurückgelegte Strecke s in Abhängigkeit von der Zeit t

Beschleunigung s-t-Diagramm

Ergebnis:

Es ergibt sich kein linearer Zusammenhang. Die Steigung (und damit die Geschwindigkeit) ist nicht konstant, sondern nimmt zu.

Der Verlauf des Graphen erinnert an eine Parabel. Die Funktionsgleichung einer (Normal-) Parabel lautet $y(x)=x^{2}$ . Das legt die Vermutung nahe, dass zwischen Strecke und Zeit ein quadratischer Zusammenhang besteht.

Vermutung: Es gilt der Zusammenhang $s\sim t^{2}$

Überprüfung:

Der vermutete Zusammenhang lässt sich sowohl rechnerisch als auch zeichnerisch überprüfen:

a) Rechnerische Überprüfung:

Wenn der Zusammenhang $s\sim t^{2}$ gilt, dann müssten die Quotienten $\dfrac {s}{t^{2}}$ konstant sein.

Dazu werden zunächst die Werte für $t^{2}$ und anschließend die Quotienten berechnet und in zwei zusätzlichen Spalten in der Tabelle notiert:

s in cm	t in s	$t^{2}$ in $s^{2}$	$\dfrac {s}{t^{2}}$ in $\dfrac {m}{s^{2}}$
0	0	–	–
20	1,11	1,23	0,162
40	1,57	2,46	0,162
60	1,96	3,84	0,156
80	2,25	5,06	0,158
100	2,50	6,25	0,16
120	2,73	7,45	0,161

Ergebnis:

Die Quotienten sind weitgehend konstant. Abweichungen können als Messfehler interpretiert werden.

Eine bessere Überprüfung liefert jedoch die grafische Methode:

b) Grafische Überprüfung:

Wenn gilt: $s\sim t^{2}$ , dann müsste sich beim Auftragen von $s$ über $t^{2}$ eine Gerade ergeben.

Zurückgelegte Strecke in Abhängigkeit vom Quadrat der benötigten Zeit

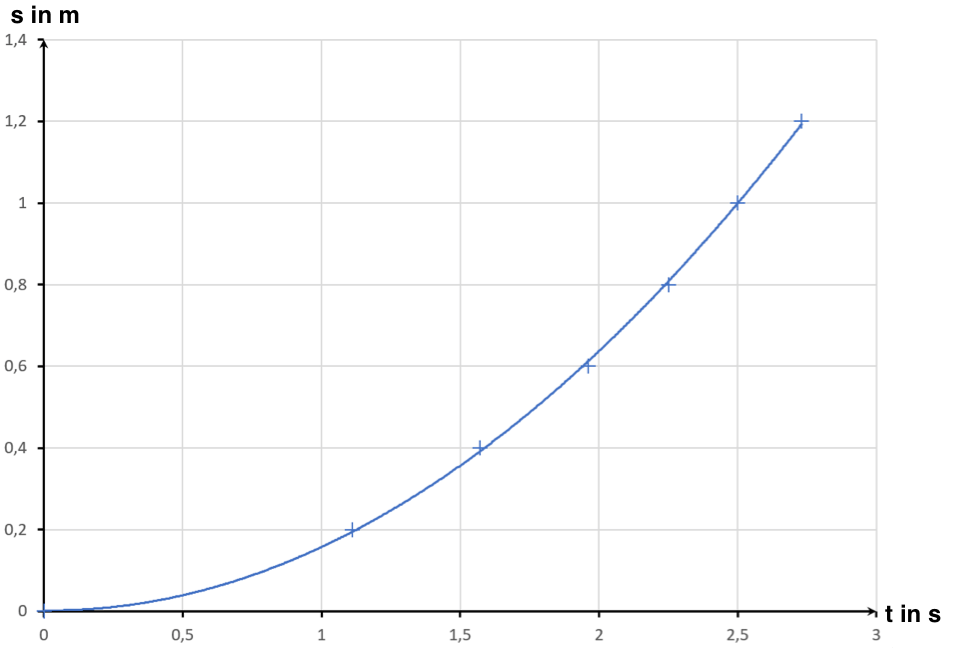
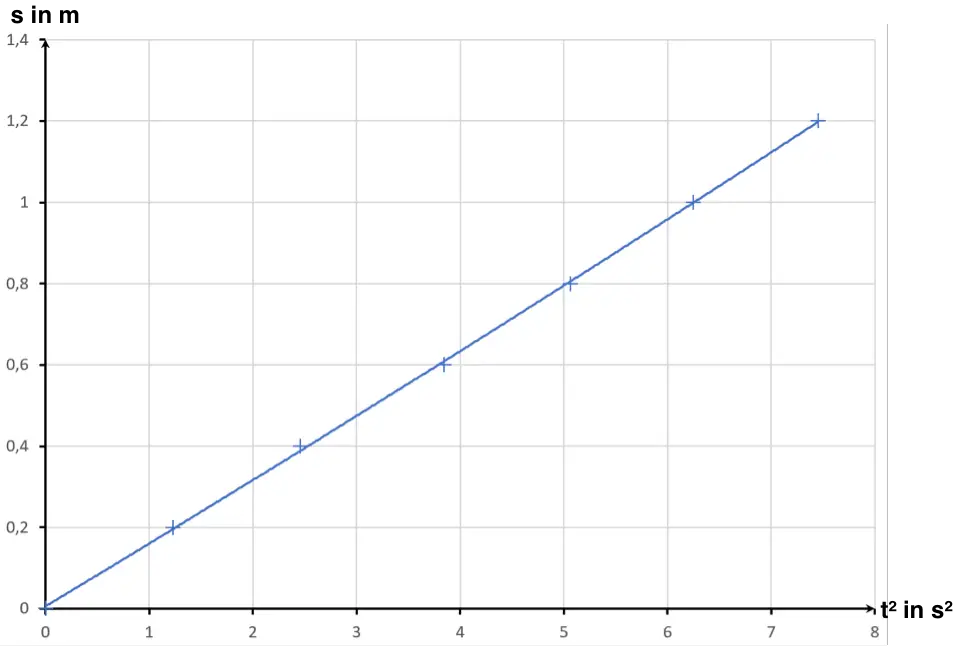
Beschleunigung s-t quadrat-Diagramm

Ergebnis:

Die Werte liegen annähernd auf einer Geraden. Wir zeichnen erneut eine Ausgleichsgerade und interpretieren die Abweichungen als Messfehler.

Damit hat sich die Vermutung bestätigt, und wir können davon ausgehen, dass folgende Zusammenhänge gelten:

$s\sim t^{2}$ bzw. $\dfrac {s}{t^{2}}$ oder $s=konst. \cdot t^{2}$

Auch hier gibt es also eine Konstante. Doch in diesem Fall ist nicht die Geschwindigkeit konstant, sondern die Zunahme der Geschwindigkeit. Diese wird als Beschleunigung bezeichnet.

Die Beschleunigung

Die Änderung der Geschwindigkeit mit der Zeit wird als Beschleunigung a bezeichnet. Diese kann sowohl positiv (Geschwindigkeitszunahme) als auch negativ (Geschwindigkeitabnahme) sein.

Definition der Beschleunigung: $a=\dfrac {\Delta v}{\Delta t}$

Die Einheit der Beschleunigung lautet: $\dfrac{\frac {m}{s}}{s}=\dfrac {m}{s^{2}}$ (gesprochen: “Meter pro Sekunde Quadrat”)

Ist die Beschleunigung konstant, spricht man von einer gleichmäßig beschleunigten Bewegung.

Um ein Gefühl für die neue physikalische Größe “Beschleunigung” zu bekommen, wollen wir zunächst die Beschleunigung eines anfahrenden Autos berechnen.

Oft wird die Zeit angegeben, die ein Auto für eine Beschleunigung aus dem Stand auf die Geschwindigkeit von 100km/h benötigt.

Beispiel:

Ein Auto beschleunigt von 0 auf 100 km/h in 6,5 Sekunden.

Wir berechnen die mittlere* Beschleunigung:

Es gilt: $a=\dfrac {\Delta v}{\Delta t}$

Damit die Einheiten stimmen, müssen wir die Geschwindigkeit in m/s umrechnen:

Es gilt: $100\, \frac {km}{h}=27,\overline {7}\, \frac {m}{s}$

Wir setzen ein und erhalten

$a=\dfrac {27,\overline {7}\, \frac {m}{s}}{6,5s}=4,27\, \frac {m}{s^{2}}$

Die Beschleunigung beträgt also $4,27\, \frac {m}{s^{2}}$ .

* Hinweis:

Die Beschleunigung eines Autos ist nicht konstant. Durch Einsetzen der gesamten Zeit sowie der Endgeschwindigkeit erhalten wir daher nur die mittlere Beschleunigung (Durchschnittsbeschleunigung).

Typische Beschleunigungswerte

Hier noch ein paar weitere Beschleunigungen aus dem Alltag:

Beispiel	Beschleunigung a (ca.)
Anfahren eines ICE	$0,47\, \frac {m}{s^{2}}$
Start eines Verkehrsflugzeuges	$2,9\, \frac {m}{s^{2}}$
Formel-1-Wagen	$11\, \frac {m}{s^{2}}$
Geschoss im Lauf	$500.000\, \frac {m}{s^{2}}$

Geschwindigkeits-Zeit-Diagramme

Bewegungen lassen sich auch in einem sog, Geschwindigkeits-Zeit-Diagramm (v-t-Diagramm) darstellen. Darin wird die Geschwindigkeit gegenüber der Zeit aufgetragen.

Für eine gleichförmige Bewegung sieht das v-t-Diagramm folgendermaßen aus:

Die Geschwindigkeit bleibt über den gesamten Zeitraum konstant. Es ergibt sich also eine Gerade, die parallel zur Zeitachse verläuft.

Bei einer gleichmäßig beschleunigten Bewegung ändert sich die Geschwindigkeit gleichmäßig. Das heißt: Die Änderung der Geschwindigkeit, also die Beschleunigung $a=\frac {\Delta v}{\Delta t}$ , ist konstant. Die Beschleunigung entspricht der Steigung im v-t-Diagramm, daher ist die Steigung konstant:

Ist die Beschleunigung über die gesamte Strecke konstant und startet der Körper aus der Ruhe, so lässt sich diese einfach berechnen mit

$a=\dfrac {v}{t}$

Die aus der Ruhe erreichte Geschwindigkeit $v$ innerhalb der Zeit $t$ ergibt sich durch einfaches Umformen:

$v=a\cdot t$

Dieser Zusammenhang wird als Geschwindigkeits-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung bezeichnet.

Geschwindigkeits-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung

Für die Anfangsbedingung t = 0 und v = 0 (Start aus der Ruhe) gilt:

${v=at}$

Welcher Zusammenhang gilt zwischen Weg und Zeit bei der gleichmäßig beschleunigten Bewegung?

Wir wissen, dass der zurückgelegt Weg proportional zum Quadrat der dafür benötigten Zeit ist:

Es gilt also $s\sim t^{2}$

Das Weg-Zeit-Gesetz einer gleichmäßig beschleunigten Bewegung hat demnach die Form

$s=konst.\cdot t^{2}$

Doch welchen Wert bzw. welche Bedeutung hat dieser konstante Faktor?

Die Geschwindigkeit v kann es nicht sein, denn zwischen Geschwindigkeit und Zeit gibt es einen linearen Zusammenhang. Vielleicht ist es die Beschleunigung a?

Um eine Antwort auf diese Frage zu finden, stellen wir folgende Überlegung an:

Wir skizzieren noch einmal je ein Geschwindigkeits-Zeit-Diagramm einer gleichförmigen sowie einer gleichmäßig beschleunigten Bewegung:

Geschwindigkeits-Zeit-Diagramme

Linkes Diagramm:

Die Geschwindigkeit sowie die Zeit entsprechen den Seitenlängen des eingezeichneten Rechtecks. Multipliziert man die Seitenlängen eines Rechtecks miteinander, so ergibt sich die Fläche des Rechtecks. In diesem Fall entspricht die Fläche unter dem Graphen dem Fakor $v\cdot t$ . Diese Faktor entspricht nach dem Weg-Zeit Gesetz der zurückgelegten Strecke s, denn es gilt:

$s=v\cdot t$

Es gilt also:

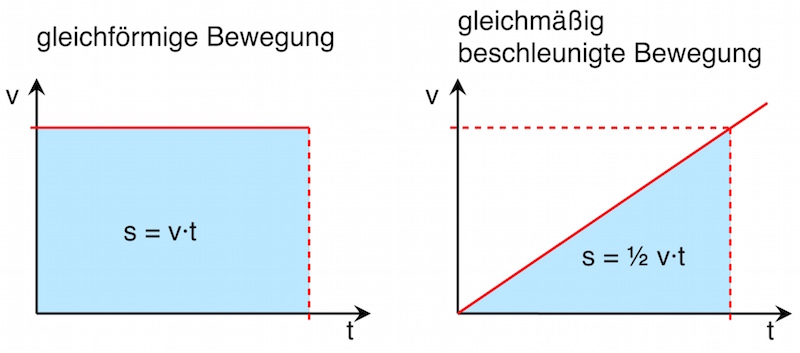
Die Fläche unter dem Graphen im v-t-Diagramm entspricht also der zurückgelegten Strecke!

Rechtes Diagramm:

Das gilt auch bei der beschleunigten Bewegung! Da die Geschwindigkeit jedoch nicht konstant ist sondern von 0 gleichmäßig ansteigt, ist die Fläche unter dem Graphen und damit die zurückgelegte Strecke s nur halb so groß und entspricht statt einem Rechteck einem Dreieck.

Offensichtlich gilt für die Fläche des Dreiecks und damit für die zurückgelegte Strecke

$s=\frac {1}{2}v\cdot t$

Für die Geschwindigkeit gilt nach dem Geschwindigkeits-Zeit-Gesetz für gleichmäßig beschleunigte Bewegungen (s.o.):

$v=a\cdot t$

Ersetzen wir die Geschwindigkeit durch diesen Ausdruck, ergibt sich für die zurückgelegte Strecke bei einer gleichmäßig beschleunigten Bewegung der Zusammenhang

$s=\frac {1}{2} (a\cdot t)\cdot t= \frac {1}{2}a\cdot t^{2}$ ,

der als Weg-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung bezeichnet wird.

Weg-Zeit-Gesetz der gleichmäßig beschleunigte Bewegung

Für die Anfangsbedingung t = 0, v = 0 und s = 0 gilt:

$s=\frac {1}{2}at^{2}$ bzw. $s=\frac {1}{2}vt$

Nun können wir sowohl den zurückgelegten Weg als auch die Geschwindigkeit bei einer gleichmäßig beschleunigten Bewegung zu jedem Zeitpunkt berechnen.

Beispielaufgaben

1. Ein Zug beschleunigt gleichmäßig aus der Ruhe mit der Beschleunigung 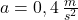$a=0,4\, \frac {m}{s^{2}}$ .

a) Welche Strecke legt er innerhalb einer Minute zurück?

Lösung:

Wir wenden das Weg-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung an:

$s=\frac {1}{2}at^{2}$

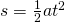
und setzen die Werte ein:

$s=\frac {1}{2}\cdot 0,4\, \frac {m}{s^{2}}\cdot \left(60\, s\right)^{2}=720\, m$

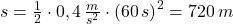
Antwort:

Die zurückgelegte Strecke beträgt 720 m.

b) Welche Geschwindigkeit hat der Zug nach einer Minute erreicht?

Lösung:

Nun benötigen wir das Geschwindigkeits-Zeit-Gesetz:

$v=at$

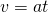
Wir setzen die Werte ein und erhalten

$v=0,4\, \frac {m}{s^{2}}\cdot 60\, s=24\, \frac {m}{s}=86,4\, \frac {km}{h}$

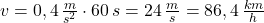
Antwort:

Die Geschwindigkeit nach einer Minute beträgt 86,4 km/h.

2. Ein Geschoss erreicht in einem 20 cm langen Lauf eine Geschwindigkeit von 2000 km/h.

a) Berechne die Beschleunigung!

Lösung:

Wir benötigen den Zusammenhang zwischen Beschleunigungsweg und Beschleunigung. Der Beschleunigungsweg s taucht nur im Weg-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung auf:

$s=\frac {1}{2}at^{2}$

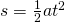
Allerdings ist die Zeit unbekannt. Daher wenden wir den zweiten bekannten Zusammenhang an, nämlich

$v=at$

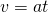
Für die Zeit t lässt sich also schreiben

$t=\dfrac {v}{a}$

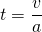
Wir ersetzen die Zeit im Weg-Zeit-Gesetz durch diesen Ausdruck und erhalten

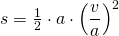$s=\frac {1}{2}\cdot a\cdot \left(\dfrac {v}{a}\right)^{2}$ bzw. $s=\frac {1}{2}\cdot a\cdot \dfrac {v^{2}}{a^{2}}$

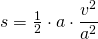
Die Beschleunigung lässt sich einmal kürzen, und wir erhalten

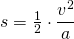$s=\frac {1}{2}\cdot \dfrac {v^{2}}{a}$ oder anders geschrieben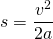 $s=\dfrac {v^{2}}{2a}$

Nun stellen wir die Gleichung nach a um und erhalten

$a=\dfrac {v^{2}}{2s}$

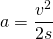
Wir setzen die Werte ein und erhalten

$a=\dfrac {\left(555,\overline {5}\, \frac {m}{s}\right)^{2}}{2\cdot 0,2\, m}=771\, 605\, \frac {m}{s^{2}}$

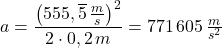
Antwort:

Die Beschleunigung beträgt 771 605 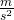$\frac {m}{s^{2}}$ .

Anderer Weg:

Wir hätten auch die fehlende Zeit berechnen und diese anschließend in die Formel einsetzen können:

Wir kennen auch den Zusammenhang

$s=\frac {1}{2}vt$

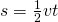
Umgestellt nach t ergibt sich

$t=\dfrac {2s}{v}$

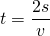
Wir setzen die Werte ein und erhalten für die Zeit

$t=\dfrac {2\cdot 0,2m}{555,\overline {5}\frac {m}{s}}=7,2\cdot 10^{-4}s$

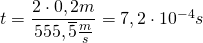
Diese Zeit setzen wir in das nach a umgestellte Weg-Zeit-Gesetz ein und erhalten das gleiche Ergebnis wie oben:

$a=\dfrac {2s}{t^{2}}=\dfrac {2\cdot 0,2m}{\left( 7,2\cdot 10^{-4}s\right)^{2}}=771\, 605\, \frac {m}{s^{2}}$

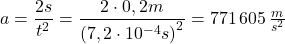
b) Nach welcher Zeit trifft das Geschoss auf ein 300 m weit entferntes Hindernis?

Lösung:

Nachdem das Geschoss den Lauf verlassen hat, wird es nicht mehr beschleunigt. Vernachlässigen wir den Luftwiderstand und die Erdbeschleunigung, können wir von einer annähernd gleichförmigen Bewegung ausgehen.

Für gleichförmige Bewegungen gilt:

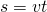$s=vt$ und damit für die Zeit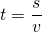 $t=\dfrac {s}{v}$

Wir setzen die Werte ein und erhalten

$t=\dfrac {300\, m}{555,\overline {5}\, \frac {m}{s}}=0,54\, s$

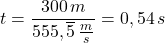
Antwort:

Das Geschoss trifft nach 0,54 Sekunden auf das Hindernis.

Achtung:

Entscheidend für die Bearbeitung dieser oder ähnlicher Aufgaben ist die klare Unterscheidung zwischen gleichförmiger und gleichmäßig beschleunigter Bewegung.

Du musst aus der Aufgabenstellung eindeutig erkennen, um welche Art der Bewegung es sich jeweils handelt und dann die gültigen Formeln verwenden.

Nur für gleichförmige Bewegungen gilt

$v=\dfrac {s}{t}$ bzw. $s=vt$

Für gleichmäßig beschleunigte Bewegungen gilt

$v=at$ sowie $s=\frac {1}{2}at^{2}$ bzw. $s=\frac {1}{2}vt$

Ein häufiger Fehler ist die Benutzung der Formeln für gleichförmige Bewegungen, obwohl es sich um eine gleichmäßig beschleunigte Bewegung handelt.

Vergleicht man das Weg-Zeit-Gesetz für beide Bewegungen, so fällt auf, dass sich dieses letztendlich nur um den Faktor $\frac {1}{2}$ unterscheidet. Der zurückgelegte Weg ist für eine bestimmte Geschwindigkeit bei einer gleichmäßig beschleunigten Bewegung aus der Ruhe innerhalb einer bestimmten Zeit genau halb so groß wie bei einer gleichförmigen Bewegung.

Dieser Zusammenhang ergibt sich direkt aus den v-t-Diagrammen (s.o.).

Eine weitere immer wieder auftretende Schwierigkeit bei dieser Art von Aufgaben ist das korrekte Umformen physikalischer Formeln. Dies ist jedoch eine der wichtigsten Fähigkeiten, die Du bei fast jeder Physikaufgabe brauchst.

Wenn Du noch Schwierigkeiten beim Umstellen von Formeln hast, dann solltest Du das unbedingt üben!

⇒ Hier findest Du eine Anleitung zum Formeln umstellen mit vielen Übungen!

Übungsaufgaben:

Cornelsen Oberstufe Physik Band 1 (1. Auflage 1998)

S. 24 A8, A9, A10

Metzler Physik SII (3. Auflage 1998)

S. 17 1. – 5.

weiter mit Der freie Fall

zurück

Gleichmäßig beschleunigte Bewegungen

Untersuchung einer nicht gleichförmigen Bewegung

Die Beschleunigung

Geschwindigkeits-Zeit-Diagramme

Geschwindigkeits-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung

Welcher Zusammenhang gilt zwischen Weg und Zeit bei der gleichmäßig beschleunigten Bewegung?

Geschwindigkeits-Zeit-Diagramme

Weg-Zeit-Gesetz der gleichmäßig beschleunigte Bewegung

Beispielaufgaben