Kurvenfahrten mit dem Auto oder Motorrad

Kurvenfahrten

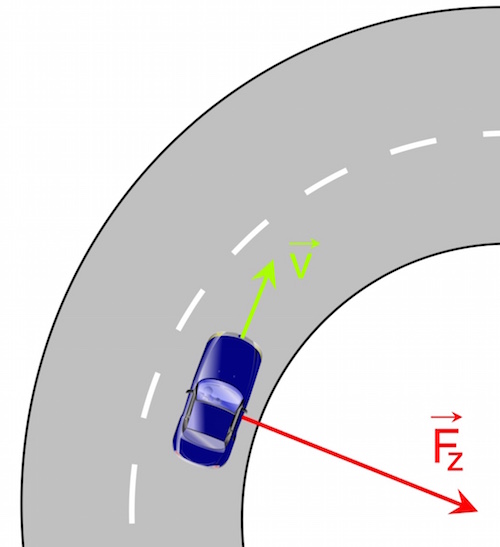
Wenn man mit dem Auto, Motorrad oder Fahrrad in eine Kurve fährt, wird die dafür notwendige Zentripetalkraft durch die Reibung zwischen Reifen und Boden aufgebracht. Die maximale Geschwindigkeit bzw. der minimale Radius, der sich durchfahren lässt, wird also durch die Reibung begrenzt.

_{Bei einer Kurvenfahrt wird die Zentripetalkraft von der Reibung aufgebracht}

Solange das Fahrzeug nicht ins Rutschen kommt, die Reifen also an der Straße haften, wirkt die Haftreibungskraft F_Haft. Diese wirkt als Zentripetalkraft.

Es gilt also:

Die Haftreibungskraft ist gleich der Zentripetalkraft: $F_{z}=F_{Haft}$

Die maximale Haftreibungskraft und damit die maximale Zentripetalkraft beträgt

$F_{Haft}=\mu_{Haft}\cdot F_{G}$

Dabei ist $\mu_{Haft}$ die Haftreibungszahl und $F_{G}$ die Gewichtskraft.

Die Haftreibungszahl $\mu_{Haft}$ hängt von den beiden Reibungspartnern (in diesem Fall: Reifen und Straße) ab.

Dabei gilt:

Je besser die Haftung, umso größer die Haftreibungszahl. Die Haftreibungszahl kann im Normalfall* maximal den Wert “1” annehmen.

Das bedeutet: Die Haftreibungskraft kann maximal so groß sein wie die Gewichtskraft.

Die Haftreibungszahl ist abhängig von der Bodenbeschaffenheit.

Für das Beispiel Reifen – Straße gelten etwa folgende Werte:

Haftreibungszahlen für verschiedene Bodenbeschaffenheiten

Reifen auf trockenem Asphalt	$\mu$ = 1,0 (optimaler Wert)
Reifen auf nassem Asphalt	$\mu$ = 0,8
Reifen auf vereister Fahrbahn	$\mu$ = 0,2

Fährt man zu schnell in eine Kurve, so reicht die Haftreibungskraft nicht aus, um die notwendige Zentripetalkraft aufzubringen. Das Fahrzeug gerät ins Rutschen, und es wirkt die (kleinere) Gleitreibungskraft. Das Fahrzeug rutscht dann tangential zum Kreisbogen so lange weiter, bis die Geschwindigkeit so klein ist, dass die Reifen wieder haften.

Berechnung der maximalen Geschwindigkeit in einer Kurve

Wie schnell ein Fahrzeug eine Kurve durchfahren kann, hängt von der Haftreibungskraft und damit von der Bodenbeschaffenheit ab sowie vom Kurvenradius.

Beispielaufgabe

Wie schnell kann ein Auto eine Kurve mit dem Radius r = 50 m auf trockener, nasser oder vereister Fahrbahn maximal durchfahren, ohne ins Rutschen zu kommen?

Die Bedingung lautet (s.o.):

Die Zentripetalkraft kann maximal so groß sein wie die Haftreibungskraft.

Es gilt: $F_{Haft}\geq F_{z}$

Wir setzen nun die Formeln für die beiden Kräfte ein:

$\mu _{Haft}\cdot F_{G}\geq m\cdot \dfrac {v^{2}}{r}$ mit $F_{G}=m\cdot g$

Auf beiden Seiten steht nun die Masse, die sich kürzen lässt:

$\mu _{Haft}\cdot \not{m} \cdot g\geq \not{m} \cdot \dfrac {v^{2}}{r}$

Daraus folgt:

Die Masse des Fahrzeuges spielt keine Rolle dabei, mit welcher Geschwindigkeit eine Kurve durchfahren werden kann!

Umgeformt nach v ergibt sich schließlich für die Bahngeschwindigkeit

$v\leq \sqrt {\mu _{Haft}\cdot r \cdot g}$

Für die o.g. Haftreibungszahlen ergeben sich folgende Werte für die maximalen Geschwindigkeiten:

Trockene Straße: $v\leq 22,1 \, \frac {m}{s}=79,7 \, \frac {km}{h}$

Nasse Straße: $v\leq 19,8 \, \frac {m}{s}=71,3 \, \frac {km}{h}$

Vereiste Straße: $v\leq 9,9 \, \frac {m}{s}=35,7 \, \frac {km}{h}$

Kurvenfahrt mit dem Motorrad

Bei der Kurvenfahrt mit eine Motorrad oder Fahrrad neigt der Fahrer das Fahrzeug zur Kurveninnenseite. Der Grund dafür ist folgender:

Das Motorrad benötigt eine zur Innenseite der Kurve gerichtete Kraft (die Zentripetalkraft).

Damit das Motorrad im Gleichgewicht bleibt und nicht umfällt, muss die Anpresskraft (die Kraft, mit der das Motorrad an die Straße gepresst wird) durch den Schwerpunkt des Motorrades verlaufen. Das wird durch die Schräglage erreicht:

Im linken Bild ist als Angriffspunkt der Kräfte der Schwerpunkt gewählt, im rechten Bild sind die Kräfte eingezeichnet, die von der Straße auf das Motorrad wirken.

Man erkennt:

Die Bodendruckkraft $\overrightarrow {F}_{B}$ (die Kraft, die von der Straße schräg nach oben auf das Motorrad wirkt), ist die vektorielle Summe aus der Zentripetalkraft $\overrightarrow {F}_{z}$ und der Gegenkraft zur Gewichtskraft $-\overrightarrow {F}_{G}$ .

Es gilt: $\overrightarrow {F}_{B}=\overrightarrow {F}_{z}-\overrightarrow {F}_{G}$

Damit die Bodendruckkraft genau durch den Schwerpunkt des Motorrads verläuft (nur dann ist das Motorrad stabil), muss für den Neigungswinkel $\varphi$ (Winkel zwischen der Senkrechten und der Bodendruckkraft) gelten:

$tan \varphi =\dfrac {F_{z}}{F_{G}}$

Mit $F_{z}=m\cdot \dfrac {v^{2}}{r}$ und $F_{G}=mg$ ergibt sich für den Neigungswinkel:

$tan \varphi =\dfrac {v^{2}}{r\cdot g}$

Auch beim Motorrad gilt prinzipiell:

Die parallel zum Boden gerichtete Komponente der Bodendruckkraft, die der Zentripetalkraft entspricht, wird durch die Haftreibung aufgebracht. Die Zentripetalkraft kann also nicht größer sein als die maximale Haftreibungskraft.

Maximaler Neigungswinkel bei Kurvenfahrt mit dem Motorrad

Für den maximalen Neigungswinkel bzw. für den Neigungswinkel bei der maximal möglichen Geschwindigkeit v_max gilt also

$F_{Z}=F_{Haft}$ und damit $tan \varphi=\dfrac {F_{Haft}}{F_{G}}$

Da der Quotient $\dfrac {F_{Haft}}{F_{G}}$ gerade der Haftreibungszahl $\mu_{Haft}$ entspricht (s.o.), folgt daraus, dass Haftreibungszahl und $tan \varphi$ gleich sind.

Für den maximalen Neigungswinkel gilt: $tan \varphi=\mu_{Haft}$

Die maximal mögliche Haftreibungszahl hat den Wert $\mu_{Haft}=1$ – in diesem Fall ist die Haftreibungskraft genauso groß wie die Gewichtskraft.

Anmerkung: In einigen Quellen findet man die Behauptung, dass die Haftreibungszahl auch deutlich größer als 1 werden kann. Die Effekte, aus denen sich derartige Werte ergeben, beruhen jedoch nicht ausschließlich auf Reibung. Weitere Hinweise dazu findest Du weiter unten*.

Für den maximalen Neigungswinkel bei optimaler Bodenhaftung gilt also

$tan \varphi =1$ und damit

$\varphi =45^{\circ}$ .

Der maximale Neigungswinkel hängt also von der Haftreibungszahl ab und kann maximal 45° betragen, solange keine weitere Effekte dazu führen, dass die Bodenhaftung vergrößert wird.*

Maximale Geschwindigkeit

Berechnet man die maximale Geschwindigkeit, mit der eine Kurve gerade noch durchfahren werden kann, erhält man durch Umstellen der Gleichung

$tan \varphi =\dfrac {v^{2}}{r\cdot g}$ (s.o.)

für die maximale Geschwindigkeit

$v=\sqrt {tan \varphi \cdot r\cdot g}$

Mit dem o.g. Zusammenhang zwischen Neigungswinkel und Haftreibungszahl

$tan\varphi=\mu_{Haft}$

erhält man schließlich die gleiche Formel, die wir zuvor schon für das Auto hergeleitet haben, nämlich

$v=\sqrt {\mu_{Haft}\cdot r\cdot g}$

* Haftreibungszahl größer als 1?

Schaut man sich Motorradrennen an, so sieht man, dass die Motorräder teilweise mit extremen Kurvenneigungen fahren. Die Neigungswinkel sind deutlich größer als 45°. Rein rechnerisch käme man mit den hier aufgestellten Formeln auf Haftreibungszahlen, die deutlich über 1 liegen.

Neben der Reibung treten jedoch weitere Effekte auf, die zu einer besseren Bodenhaftung führen:

Die Reifen der Motorräder bei derartigen Rennen sind sehr weich und umschließen (bei genügend hoher Temperatur) praktisch die Unebenheiten innerhalb der Straße. Man spricht dabei von “Mikroverzahnung”.

Zusätzlich treten außerdem Adhäsionskräfte auf. Unter Adhäsion versteht man die Anziehung der Moleküle zwischen Materialien, wenn diese sich sehr nahe kommen. Aus diesem Grund haftet Frischhaltefolie an glatten Oberflächen. Das hat jedoch nichts mit dem zu tun, was man in der Physik unter “Reibung” versteht.

Das Resultat aller Faktoren, die bei der Haftung der Reifen auf der Straße eine Rolle spielen, werden häufig mit dem Begriff “Grip” bezeichnet. Dies ist jedoch kein physikalischer Begriff.

Eine umfangreiche Erklärung zu diesem Thema findest Du unter

https://www.motorradonline.de/ratgeber/alles-ueber-schraeglage-schraeg-schraeger-am-schraegsten/

Unabhängig von den weiteren genannten Effekten gibt es jedoch eine Möglichkeit, eine Kurve schneller als mit der Geschwindigkeit $v=\sqrt {\mu_{Haft}\cdot r\cdot g}$ bzw. $v=\sqrt {tan \varphi \cdot r\cdot g}$ zu durchfahren:

Die Kurve muss überhöht werden.

Überhöhte Kurve

Durch die Überhöhung der Kurve kann diese schneller durchfahren werden, da die Zentripetalkraft nicht mehr allein durch die Haftreibungskraft aufgebracht werden muss, sondern die Bodendruckkraft einen Teil oder sogar die gesamte Zentripetalkraft aufbringt.

Im Idealfall entspricht die Resultierende aus Gewichtskraft F_G und Zentripetalkraft F_z genau der Normalkraft F_N (Kraft, die senkrecht auf die Straße wirkt). Dann gibt es keine Kraftkomponente, die parallel zur Straße verläuft, so dass keine Reibung erforderlich ist.

Ein Auto durchfährt ohne Reibung eine überhöhte Kurve

Es gilt die Bedingung:

$\overrightarrow {F}_{N}=\overrightarrow {F}_{G}-\overrightarrow {F}_{z}$ bzw.

$\overrightarrow {F}_{N}=\overrightarrow {F}_{G}+\overrightarrow {F}_{z}$ (wenn man für $\overrightarrow {F}_{z}$ die zur Zentripetalkraft entgegengerichtete Zentrifugalkraft verwendet.)

und damit

$tan \varphi=\dfrac {F_{z}}{F_{G}}=\dfrac {v^{2}}{rg}$

Damit ergibt sich für die Geschwindigkeit der gleiche Zusammenhang, den wir schon oben hergeleitet haben:

$v=\sqrt {tan \varphi \cdot r\cdot g}$

Mit dieser Geschwindigkeit könnte das Auto praktisch ohne Haftreibung eine Kurve mit dem Neigungswinkel $\varphi$ durchfahren. Die notwendige Zentripetalkraft wird durch die Normalkraft aufgebracht.

Ist die Geschwindigkeit etwas größer oder kleiner, so wäre wieder Haftreibung nötig, jedoch weniger als ohne Überhöhung der Kurve.

Der optimale Winkel $\varphi$ , bei dem keine Reibung notwendig ist, ist dabei der gleiche, mit dem sich der Motorradfahrer oder Radfahrer bei gleicher Geschwindigkeit in die Kurve lehnt (s.o.). Er tut dies instinktiv richtig, ansonsten würde er umfallen.

weiter mit Energie und Energieerhaltung

zurück