Beugung und Interferenz von Licht

Beugung von Licht am Einzelspalt

Um die Beugung von Licht nachzuweisen, wird folgendes Experiment durchgeführt:

Versuch:

Ein schmaler Spalt mit einem Laser bestrahlt. Dahinter befindet sich ein Schirm.

Ein Laser sendet einfarbiges (= monochromatisches) stark gebündeltes Licht hoher Intensität aus.

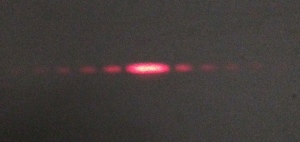
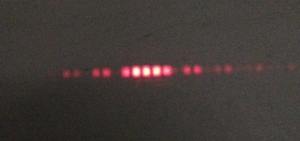
Auf dem einige Meter dahinter stehenden Schirm wird der Leuchtfleck beobachtet. Die Breite des Spaltes wird langsam immer weiter verkleinert.

Beobachtung:

Bei Verkleinerung der Spaltbreite wird der Lichtfleck breiter!

Außerdem entstehen Dunkelstellen, die auf Interferenz hinweisen.

Erklärung:

Das Licht wird an den Kanten des Einzelspalts gebeugt.

Damit haben wir gezeigt: Auch bei Licht tritt Beugung auf!

Interferenz von Licht am Doppelspalt

Nun soll das Licht einer Lichtquelle (Laser) durch einen sog. Doppelspalt (zwei schmale Spalte in sehr kleinem Abstand zueinander) aufgeteilt und anschließend zur Überlagerung gebracht werden.

Versuch:

Der Einzelspalt wird durch einen Doppelspalt ersetzt.

Der Abstand der beiden Spalte beträgt ca. 0,3mm, die Breite der beiden Spalte ca. 0,1mm.

Beobachtung:

Auf dem Schirm sind helle und dunkle Streifen zu sehen. In der Mitte liegt eine helles Maximum, daneben sind Minima (Dunkelstellen) und weitere Maxima zu erkennen.

Einige Maxima sind nur sehr lichtschwach oder scheinen komplett zu fehlen.

Erklärung:

Die beiden Wellensysteme überlagern sich und ergeben ein stabiles, räumlich verteiltes Interferenzmuster.

Auch bei Licht tritt Interferenz auf!

Erklärung des Musters auf dem Schirm

Das entstehende Muster auf dem Schirm bezeichnet man auch als Beugungsbild.

An jedem der beiden Spalte tritt Beugung auf. Das bedeutet, dass sich das Licht hinter jedem Spalt in alle Richtungen ausbreitet. Man kann unendlich viele Teilstrahlen von jedem Spalt aus annehmen.

Um die Maxima bzw. Minima (Dunkelstellen) auf dem Schirm zu erklären, sucht man sich zwei Teilstrahlen 1 und 2 heraus, die zu einem bestimmten Punkt P auf dem Schirm führen.

Man erkennt: Die beiden Teilstrahlen legen bis zum Punkt P unterschiedlich lange Wege zurück:

Der Abstand zwischen den beiden Spalten wird mit g bezeichnet, der Abstand zwischen Doppelspalt und Schirm mit a.

Hinweis: Diese Skizze ist natürlich nicht maßstabsgerecht – der Abstand a zwischen Doppelspalt und Schirm ist um ein Vielfaches größer als der Abstand g der beiden Spalte!

Zu jedem Punkt auf dem Schirm haben die beiden Teilstrahlen 1 und 2 verschieden lange Wege zurückzulegen. Nur in der Mitte M des Beugungsbildes ist der Weg für beide Teilstrahlen gleich lang – die Wellen sind in Phase. Daher trifft dort Wellenberg auf Wellenberg bzw. Wellental auf Wellental, und die Teilstrahlen interferieren konstruktiv. Es entsteht ein Maximum, das sogenannte Hauptmaximum.

Für alle anderen Punkte auf dem Schirm gibt es dagegen stets einen Wegunterschied Δs zwischen den beiden Teilstrahlen.

Durch diesen Wegunterschied Δs (s. Skizze) entsteht ein Gangunterschied δ (oft auch als Δs bezeichnet) zwischen den beiden Teilstrahlen. Von diesem Gangunterschied hängt der Schwingungszustand (die Phasenlage der beiden Teilstrahlen) und damit die Helligkeit im jeweiligen Punkt ab.

Info:

In diesem Fall ist der optische Gangunterschied δ gleich dem Wegunterschied Δs. Das muss jedoch nicht immer so sein. Ein optischer Gangunterschied kann z.B. auch bei der Reflexion oder beim Durchgang von Licht durch ein anderes optisches Medium entstehen.

Entscheidend dafür, ob es zu konstruktiver oder destruktiver Interferenz kommt, ist immer die Phasenlage der interferierenden Wellen.

Je nach Gangunterschied kommt es bei der Überlagerung zu einer Verstärkung (konstruktive Interferenz) oder Abschwächung (destruktive Interferenz) des Lichts.

Unter bestimmten Bedingungen kommt es zur maximalen Verstärkung oder zur kompletten Auslöschung (s. auch Wellenphänomene / Überlagerung von Wellen):

Bedingungen für Auslöschung und maximale Verstärkung

Bis zur Mitte legen beide Teilstrahlen den gleichen Weg zurück. Daher ist dort der Gangunterschied 0, und es kommt zur maximalen Verstärkung.

Das nächste Maximum entsteht, wenn der Gangunterschied genau einer Wellenlänge entspricht ( $\delta=\lambda$ ). Dann trifft erneut Wellenberg auf Wellenberg und Wellental auf Wellental.

Allgemein gilt:

Maximale Verstärkung (konstruktive Interferenz) entsteht, wenn der Gangunterschied $\delta$ Null oder ein ganzzahliges Vielfaches der Wellenlänge λ beträgt.

Bedingung für Verstärkung (konstruktive Interferenz):

$\delta=k\cdot \lambda$ mit k = 0, 1, 2, 3, …

Bei k = 0 spricht man vom Maximum 0. Ordnung oder Hauptmaximum.

Die Maxima für k = 1, 2, … werden Maximum 1., 2. bzw. k-ter Ordnung genannt.

Das erste Minimum entsteht, wenn der Gangunterschied gerade eine halbe Wellenlänge beträgt.

Allgemein gilt:

Es kommt zur Auslöschung (destruktive Interferenz), wenn der Gangunterschied ein ungeradzahliges Vielfaches der halben Wellenlänge λ/2 beträgt.

Bedingung für Auslöschung (destruktive Interferenz):

$\delta=(2k+1)\dfrac{\lambda}{2}$ mit k = 0, 1, 2, 3, …

oder

$\delta=(2k-1)\dfrac{\lambda}{2}$ mit k = 1, 2, 3, 4, …

Bei $\delta=\frac {\lambda}{2}$ spricht man vom Minimum 1. Ordnung. Die weiteren Minima werden entsprechend als Minimum 2., 3., … k-ter Ordnung bezeichnet.

Liegt Punkt P genau im Zentrum des Maximums 1. Ordnung, muss also für den Wegunterschied und damit den Gangunterschied gelten:

$\Delta s=\lambda$ bzw. $\delta=\lambda$

Für den Fall, dass Punkt P im ersten Minimum liegt, gilt:

$\delta=\dfrac {\lambda}{2}$

Mit Hilfe dieser Überlegungen und durch Messen bestimmter Größen ist es möglich, mit dem Doppelspaltversuch die Wellenlänge des verwendeten Lichts zu bestimmen.

weiter mit Bestimmung der Wellenlänge von Licht

zurück