Energie eines geladenen Kondensators

Wie viel Energie ist in einem geladenem Kondensator gespeichert?

Ein Kondensator ist ein Ladungs- und Energiespeicher. Beim Laden und Entladen eines Kondensators wird Ladung transportiert, wodurch die Spannung am Kondensator steigt bzw. sinkt. Die Kapazität eines Kondensators gibt dabei an, welche Ladungsmenge bei einer bestimmten Spannung aufnehmen kann.

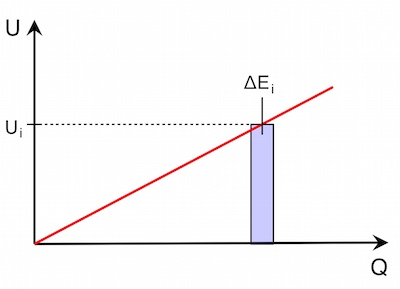
Für die Arbeit W beim Laden gilt für ein Ladungselement :

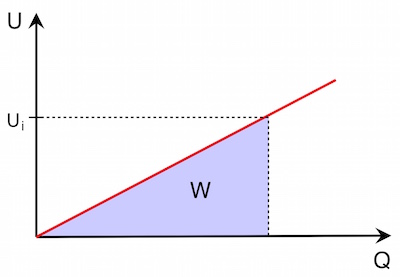
Grafisch dargestellt:

^{Im U-Q-Diagramm entspricht die Fläche unter der Kurve der beim Aufladen verrichteten Arbeit}

^{und damit der im Feld gespeicherten Energie.}

Die Gesamtarbeit W ergibt sich aus der Summe der Teilarbeiten.

Da die Spannung beim Laden bzw. Entladen nicht konstant ist, sondern die Spannung proportional zur Ladungsmenge steigt, gilt hier nicht   – für jedes Ladungselement muss mit Steigung der Spannung immer mehr Arbeit verrichtet werden.

Für den dargestellten Fall ergibt sich: Die Fläche unter der Kurve entspricht der verrichteten Arbeit und damit der Hälfte gegenüber dem Fall, dass die Spannung konstant wäre. Es gilt demnach:

mit      

ergibt sich für die gesamte verrichtete Arbeit

Da die verrichtete Arbeit gleich der Energieänderung ist, gilt für die im Plattenkondensator gespeicherte Feldenergie:

 bzw.  

Beispielaufgabe:

Bei Blitzgeräten von Fotoapparaten werden Kondensatoren als Energiespeicher genutzt.

a) Wie groß ist die im Kondensator gespeicherte und beim Auslösen des Blitzes frei werdende Energie, wenn der eingebaute Kondensator eine Kapazität von 100 mF hat und die Ladespannung 6 V beträgt?

b) Warum kann ein zweiter Blitz erst nach einer bestimmten Zeit ausgelöst werden?

Analyse:

a) Die im Kondensator gespeicherte Energie kann aus Kapazität und Ladespannung berechnet werden.

Gesucht:

Gegeben:  ,    

Lösung:

Für die Energie eines geladenen Kondensators gilt:

Einsetzen der Werte ergibt

und damit

Ergebnis:

a) Im Kondensator des Blitzgerätes ist eine Energie von 1,8 J gespeichert.

b) Unmittelbar nach dem Zündvorgang ist der Kondensator entladen. Die Feldenergie ist null. Für den erneuten Aufladevorgang ist eine bestimmte Zeit erforderlich, die von der Kapazität des Kondensators und vom ohmschen Widerstand im Stromkreis abhängig ist. Erst nach vollständigem Aufladen ist das Blitzgerät wieder betriebsbereit.