Zustandsänderungen

Dehnt sich ein Gas durch Zufuhr von Wärme aus, so kann es mechanische Arbeit verrichten, wie z.B. den Kolben in einem Verbrennungsmotor bewegen.

Der 1. Hauptsatz der Thermodynamik gilt für alle Zustandsänderungen eines idealen Gases.

Wir betrachten verschiedenen Zustandsänderungen und überlegen, wie sich die dabei ausgetauschte Energie erfassen lässt.

Isobare Zustandsänderungen (Expansion und Kompression)

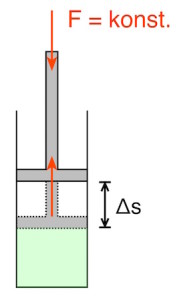
Wird einem Gas Wärme zugeführt, so expandiert es, solange nicht auch der Druck zunimmt. Dadurch kann das Gas z.B. den Kolben eines Zylinders, indem das Gas eingeschlossen ist, herausschieben und so mechanische Arbeit verrichten.

Bleibt der Druck konstant, spricht man von einer isobaren Expansion.

Kühlt das Gas ab, so zieht es sich zusammen. Bleibt der Druck dabei konstant, handelt es sich um eine isobare Kompression. Der Stempel wird wieder in den Kolben hineingezogen.

Die bei einer isobaren Expansion vom Gas verrichtete Arbeit lässt sich recht einfach erfassen:

Isobare Expansion

Wird der Stempel um die Strecke \Delta s nach oben gedrückt, so beträgt die verrichtete Arbeit

W=F\cdot \Delta s

Der (konstante) Druck ergibt sich aus dem Quotienten aus Kraft und Fläche: p=\dfrac {F}{A}

Damit gilt für die Kraft:   F=p\cdot A

Außerdem entspricht das Produkt aus der Strecke \Delta s und der Fläche A des Zylinders der Volumenänderung \Delta V:

A\cdot \Delta s=\Delta V

Die verrichtete Arbeit beträgt also

W=p\cdot \Delta V

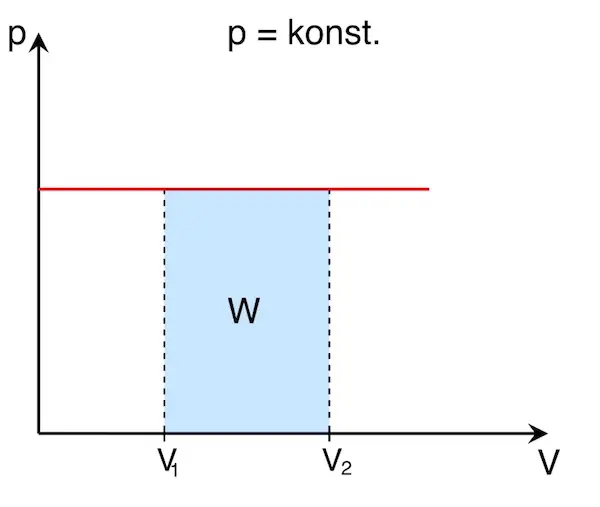
Ist der Druck wie in diesem Beispiel konstant, lässt sich die Arbeit W leicht berechnen oder im p-V-Diagramm ablesen:

Arbeit im p-V-Diagramm konstanter Druck

Die Fläche unter der Kurve im p-V-Diagramm entspricht der verrichteten Arbeit W. Da sich das Volumen beim Verrichten der Arbeit ändert, spricht man auch von Volumen(änderungs)arbeit.

Isotherme Zustandsänderungen (Kompression und Expansion)

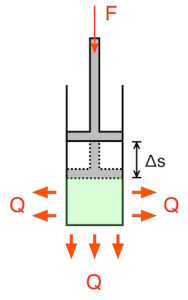
Wird der Stempel durch Verrichten mechanischer Arbeit in den Zylinder hineingedrückt, so verringert sich das Volumen, der Druck nimmt zu, und die Temperatur steigt.

Das Gas gibt anschließend die Wärme an die Umgebung ab, bis es seine ursprüngliche Temperatur erreicht.

Isotherme Kompression

Wird die Kompression so langsam ausgeführt, dass der Wärmeaustausch für einen Gleichgewichtszustand sorgt, so bleibt die Temperatur konstant – es handelt sich dann um eine isotherme Kompression.

Verläuft der Prozess umgekehrt – verrichtet also das Gas durch Expansion mechanische Arbeit, und bleibt die Temperatur dabei konstant – so handelt es sich um eine isotherme Expansion.

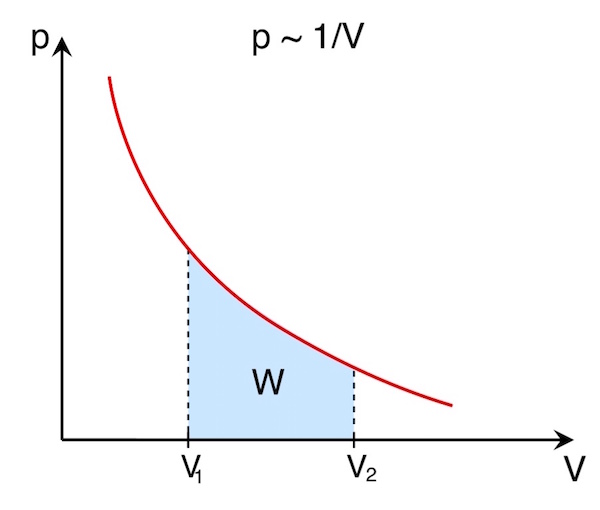
Für eine isotherme Zustandsänderung ergibt sich im p-V-Diagramm folgender Zusammenhang (vgl. Gasgesetze):

Arbeit im p-V-Diagramm Druck nicht konstant

Auch hier entspricht die bei der Volumenänderung \Delta V verrichtete Arbeit W der Fläche unter der Kurve. Die verrichtete Arbeit ist offensichtlich umso größer, je größer die Volumenänderung \Delta V=V_{2}-V_{1} ist.

Da der Druck nicht konstant ist, muss die verrichtete Arbeit mit einem Integral berechnen:

W=-\int\limits_{V_{1}} ^{V_{2}}p\,dV     bzw.    W=\int\limits_{V_{1}} ^{V_{2}}p\,dV

(Das Vorzeichen hängt davon ab, ob Arbeit an dem Gas verrichtet wird oder das Gas Arbeit verrichtet.)

Aus der universellen Gasgleichung  pV=nRT  ergibt sich für den Druck

p=\dfrac {nRT}{V}

und damit für die verrichtete Arbeit

W=-nRT\int\limits_{V_{1}} ^{V_{2}}\dfrac {dV}{V}=-nRT \;ln\dfrac {V_{2}}{V_{1}}

Nach dem ersten Hauptsatz entspricht die (bei der Expansion) zugeführte oder (bei der Kompression) abgegebene Wärme Q der verrichteten Arbeit W.

weiter mit Kreisprozesse
zurück