Schwingungen kommen in vielfältiger Weise in der Natur und in unserem Alltag vor.
Beispiele für Schwingungen:
Schaukel
Pendel einer Uhr
Federschwingung
Schwingung einer Stimmgabel
Schwingung einer Gitarrensaite
…
Jede Schwingung zeichnet sich dadurch aus, dass ein Körper eine zeitlich periodische Bewegung um eine Gleichgewichtslage ausführt.
Eine mechanische Schwingung ist eine zeitlich periodische Bewegung eines Körpers um eine Gleichgewichtslage (Ruhelage).
Eigenschaften einer Schwingung:
Eine Schwingung entsteht, wenn ein Körper, der beweglich (aber nicht frei beweglich) gelagert ist, aus einer Gleichgewichtslage ausgelenkt wird und es eine rücktreibende Kraft gibt, die ihn wieder in Richtung Ruhelage zurückzieht.
Beispiele für eine solche rückreibende Kraft (auch Rückstellkraft genannt):
Bei einem Federpendel: Zugkraft der Feder
Bei einem Fadenpendel: Gewichtskraft
Zur Beschreibung einer Schwingung bieten sich folgende Größen an:
| Bezeichnung | Symbol | Bedeutung | Einheit |
| Auslenkung (Elongation) | y | Abstand zur Ruhelage | m, cm |
| Amplitude | ymax | Maximale Auslenkung aus der Ruhelage | m, cm |
| Schwingungsdauer (Periodendauer) | T | Dauer für einen Schwingungsvorgang
(Dauer einer Periode) |
s |
| Frequenz | f | Anzahl der Schwingungen pro Sekunde | Hz = 1/s |
Hinweis:
Statt 
wird für die Auslenkung auch häufig das Formelzeichen 
(wie für Strecke) verwendet, für die Amplitude entsprechend 
.
Auch gebräuchlich für die Amplitude sind statt 
bzw. die Bezeichnungen 
(sprich: y-Dach) bzw. 
.
Ein Beispiel für eine Schwingung ist eine Federschwingung:
Ein Gewichtsstück hängt an einer Schraubenfeder und wird ausgelenkt. Lässt man es los, so führt das Gewicht eine vertikale Schwingung um die Ruhelage aus.
Die Ruhelage oder Gleichgewichtslage ist der Ort, an dem das Gewichtsstück in Ruhe hängt, wenn man es nicht auslenkt.
Stellt man die Auslenkung y in Abhängigkeit von der Zeit t dar, so ergibt sich eine Sinusfunktion.
Das folgende Diagramm ist mit Hilfe eines Ultraschallsensors entstanden:
Ein Ultraschallsensor, der unter einem an einer Schraubenfeder hängenden Gewicht positioniert wurde, misst in kurzen Zeitabständen den Abstand des Gewichts zum Sensor.
Die Abstände zum Sensor sind auf der senkrechten Achse (in m) aufgetragen, jeder Punkt entspricht einer Messung. Auf der horizontalen Achse ist die Zeit (in s) aufgetragen:
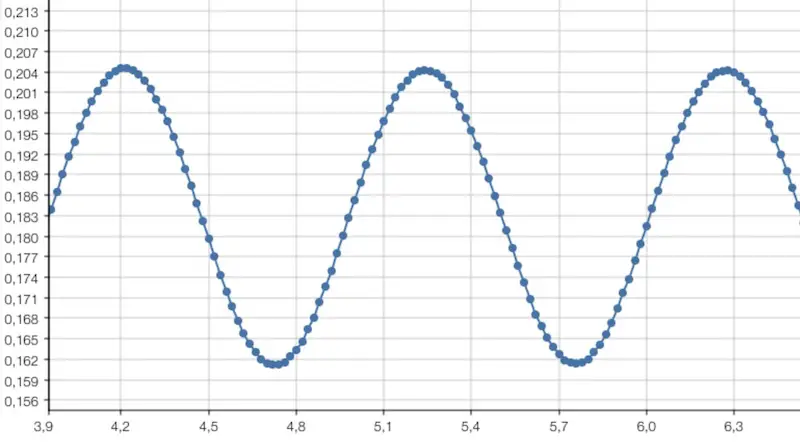
Eine Schwingung, bei der die Weg-Zeit-Funktion eine Sinusfunktion ist, bezeichnet man als harmonische Schwingung. Ein Federpendel führt also eine harmonische Schwingung aus.
Auch eine Stimmgabel führt annähernd eine harmonische Schwingung aus. Einen Ton, der durch eine harmonische Schwingung entsteht, bezeichnet man daher als Sinuston.
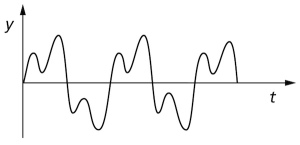
Bei der Schwingung von Saiten oder Resonanzkörpern von Musikinstrumenten sowie von Stimmbändern handelt es sich nicht um harmonische Schwingungen – die entsprechenden Schwingungsbilder zeigen keine Sinusfunktion.
Beispiel für eine nicht harmonische Schwingung:
Ohne Reibung bliebe die Amplitude über die Zeit erhalten, das heißt, die maximale Auslenkung bliebe mit der Zeit konstant.
Eine Schwingung, bei der die Amplitude bei jedem Schwingungsvorgang konstant bleibt, bezeichnet man als ungedämpfte Schwingung.
Reale Schwingungen kommen allerdings durch Reibungseinflüsse nach einiger Zeit zur Ruhe – die Amplitude wird bei jedem Schwingungsvorgang kleiner. Man nennt sie daher gedämpfte Schwingungen.
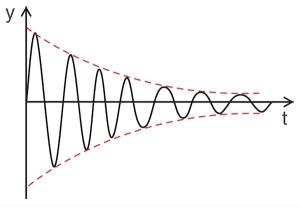
gedämpfte Schwingung
Die Dämpfung beim Federpendel resultiert aus der inneren Reibung innerhalb der Feder, Reibung bei der Aufhängung sowie Luftreibung. Ist die Dämpfung klein und der betrachtete Zeitraum kurz, kann eine solche Schwingung näherungsweise als ungedämpfte Schwingung betrachtet werden.
Genauere Informationen und Herleitungen zu gedämpften Schwingungen erhältst Du im entsprechenden Abschnitt “Gedämpfte Schwingungen“.