Gedämpfte Schwingungen - Schwingungsgleichung

Beschreibung von gedämpften Schwingungen

Bei jeder Schwingung treten durch unterschiedliche Arten von Reibung Energieverluste auf. Dadurch wird die Amplitude ständig kleiner, bis die Schwingung schließlich zur Ruhe kommt. Bei einer solchen Schwingung spricht man von einer gedämpften Schwingung.

Um zu untersuchen, wie sich bei einer gedämpften Schwingung die Amplitude mit der Zeit ändert, wird die Amplitude für mehrere aufeinanderfolgende Schwingungsvorgänge abgelesen und notiert.

Ergebnis:

n	0	1	2	3	4	5	6	7
y_{max, n} in cm	15,0	10,2	6,9	4,7	3,2	2,2	1,5	1,0

Die Anfangsamplitude wird mit $y_{max,0}$ bezeichnet.

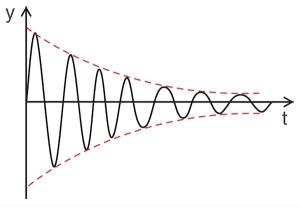
Trägt man die Elongation in Abhängigkeit von der Zeit grafisch dar, ergibt sich für eine gedämpfte Schwingung folgender Verlauf:

y(t)-Funktion einer gedämpften Schwingung

Der Verlauf der Amplitude in Abhängigkeit von der Zeit (rote Kurve) erinnert an eine abnehmende Exponentialfunktion.

Um zu überprüfen, ob es sich tatsächlich um eine Exponentialfunktion handelt, ermitteln wir jeweils den Quotienten zweier aufeinanderfolgender Amplituden. Bei einer Exponentialfunktion müsste dieser konstant sein.

n	0	1	2	3	4	5	6	7
y_n in cm	15,0	10,1	6,9	4,7	3,2	2,2	1,5	1,0
y_n+1 / y_n	0,67	0,68	0,68	0,66	0,69	0,68	0,67

Ergebnis:

1. Der Quotient y_n+1 / y_n zweier aufeinander folgender Amplituden ist weitgehend konstant.

2. Die Zeit, in der die Amplitude jeweils auf die Hälfte eines willkürlich gewählten Anfangswertes sinkt, ist ebenfalls konstant. Man nennt diese Zeit Halbwertszeit der Schwingung.

Diese Ergebnisse bekräftigen die Vermutung, dass es sich um eine exponentielle Abnahme handelt.

Für eine genauere Überprüfung gibt es folgende Möglichkeiten:

1. Man erstellt mit einem Tabellankalkulationsprogramm ein Diagramm der Messwerte und lässt sich die Funktion für eine Exponentialfunktion anzeigen.

Diese hat die Form $y_{max}=y_{max,0}\cdot e^{-Konstante\cdot x}$ .

Da es sich in diesem Fall um eine Funtion der Zeit handelt, gilt:

$y_{max}(t)=y_{max,0}\cdot e^{-Konstante\cdot t}$

2. Man stellt den natürlichen Logarithmus der Amplitude $ln\, y_{max}$ in Abhängigkeit von der Zeit dar. Ergibt sich eine Gerade, so bestätigt dies, dass es sich um eine Exponentialfunktion handelt.

Die Überprüfungen bestätigen die Vermutung, dass es sich um eine Exponentialfunktion der Form $y_{max}=y_{max,0}\cdot e^{-Konstante\cdot t}$ handelt.

Die Konstante im Exponenten sagt etwas darüber aus, wie schnelle die Amplitude kleiner wird, also wie stark die Dämpfung ist.

Wir nennen sie deshalb Dämpfungkonstante k. Damit lautet die Exponentialfunktion:

$y_{max}=y_{max,0}\cdot e^{-k\cdot t}$

Die Gleichung der Geraden der logarithmischen Funktion heißt

$ln\, y_{max}(t)=ln\, y_{max,0}-kt$

Durch Entlogarithmieren erhält man

$y_{max}(t)=y_{max,0}\cdot e^{-kt}$

und damit die gleich Funktion wie oben.

Diese Exponentialfunktion beschreibt die zeitliche Abnahme der Amplitude einer gedämpften Schwingung.

Um die Auslenkung einer gedämpften Schwingung in Abhängigkeit von der Zeit zu beschreiben, muss man nun in der Schwingungsgleichung für harmonische Schwingungen die Amplitude $y_{max}$ durch den Ausdruck $y_{max}=y_{max,0}\cdot e^{-kt}$ ersetzen – denn diese ist ja bei gedämpften Schwingungen nicht konstant, sondern sie wird kleiner.

Damit erhält man $y(t)=y_{max,0}\cdot e^{-kt}\cdot sin\, \omega t$ bzw. $y(t)=y_{max,0}\cdot e^{-kt}\cdot cos\, \omega t$

Da die Anfangsamplitude $y_{max,0}$ die Amplitude zum Zeitpunkt t = 0 ist, ist die Kosinusvariante in diesem Fall sinnvoller. Grundsätzlich lässt sich aber auch jede andere Amplitude als Anfangsamplitude verwenden.

Gedämpfte harmonische Schwingung

Bei einer geschwindigkeitsabhängigen* Dämpfung ist der Quotient zweier aufeinander folgender Amplituden einer harmonischen Schwingung konstant.

Das Zeit-Elongationsgesetz einer gedämpften harmonischen Schwingung lautet

$y(t)=y_{max,0}\cdot e^{-kt}\cdot cos\, \omega t$

(für die Anfangsbedingung $y=y_{max}$ bei $t=0$ )

bzw.

$y(t)=y_{max,0}\cdot e^{-kt}\cdot sin\, \omega t$

(für die Anfangsbedingung $y=0$ bei $t=0$ )

Eine ausführlichere Herleitung der Schwingungsgleichung für gedämpfte Schwingungen kannst Du hier herunterladen!

* Die geschwindigkeitsabhängige Dämpfung ist die häufigste Form der Dämpfung. Dabei ist die Reibung, die für Dämpfung verantwortlich ist, von der Geschwindigkeit abhängig. Das ist z.B. bei der Luftreibung oder auch der Reibung im Wasser der Fall.

Kommt die Dämpfung durch Reibung zwischen Festkörpern zustande, ist die Reibungskraft von der Geschwindigkeit unabhängig. Der Abfall der Amplitude erfolgt dann nicht exponentiell, sondern linear.

weiter mit Erzwungene Schwingungen

zurück