Interferenz am Einzelspalt

Auch am Einzelspalt gibt es Interferenz

Bei der Beugung am Einzelspalt fiel uns bereits auf, dass das Beugungsbild von dunklen Stellen unterbrochen war, was auf Interferenz hindeutet:

Doch wie kann es bei nur einem Spalt zur Interferenz kommen? Woher kommen die Minima?

Nun, die Spaltbreite l ist auch bei einem schmalen Spalt im Vergleich zur Wellenlänge relativ groß. Jeder Punkt im Spalt kann als Ausgangspunkt einer Elementarwelle angesehen werden,

Man kann beliebig viele Teilstrahlen innerhalb des Spalts annehmen.

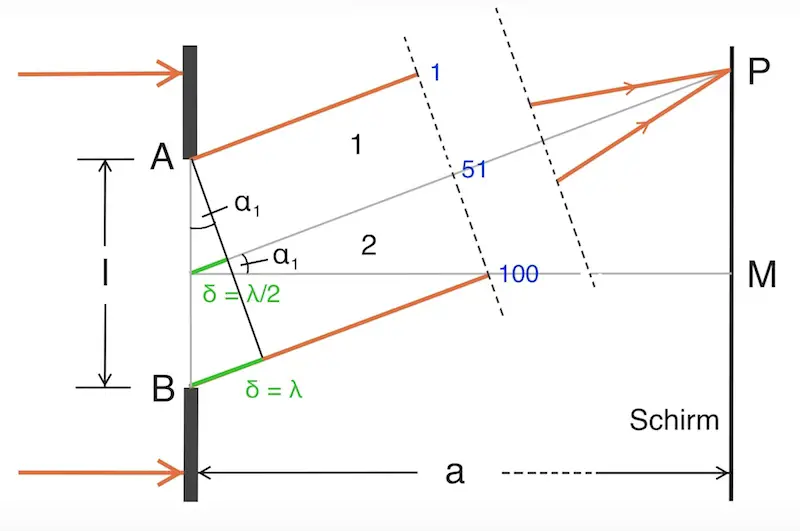
Zur Erklärung der Minima greift man ein Bündel paralleler Lichtstrahlen heraus, die alle zum ersten Minimum (Punkt P) führen:

Man teilt nun das Bündel in zwei Teilbündel 1 und 2 ein.

Haben die Randstrahlen zueinander den Gangunterschied λ (s. Skizze), dann findet jeder Strahl des Teilbündels 1 im Teilbündel 2 einen Partner mit dem Gangunterschied λ/2, mit dem er sich auslöscht.

Die Anzahl der Teilstrahlen kann man dabei beliebig hoch ansetzen.

Beispiel:

Bei 100 Teilstrahlen hat der mittlere – also der 51. – zum ersten Randstrahl einen Gangunterschied von λ/2; die beiden Strahlen löschen sich also gegenseitig aus.

Das gleiche gilt für den 2. und 52., den 3. und 53., …, den 50. und 100. Teilstrahl.

Somit löschen sich alle Teilstrahlen komplett aus – es entsteht ein Minimum.

Die Bedingung für ein Minimum ist also, dass die Randstrahlen einen Gangunterschied von $\delta=k\cdot \lambda$ haben müssen.

Dann gilt: $\dfrac {k\lambda}{l}=sin\alpha_{k}$

Minima durch Interferenz am Einzelspalt

Bei der Beugung von Licht am Einzelspalt entstehen dunkle und helle Streifen.

Bei einer Spaltbreite von l gilt für den Winkel $\alpha_{k}$ zu den Minima

$sin\alpha_{k}=\dfrac {k\lambda}{l}$ mit k = 1,2,3,…, < $\dfrac {l}{\lambda}$

( $\delta=k\lambda$ kann nicht größer als $l$ sein)

Die Effekte des Einzelspaltes sind auch beim Doppelspalt sichtbar.

Da ein Doppelspalt aus zwei Einzelspalten besteht, ist das Interferenzmuster der Einzelspalte auch beim Doppelspalt sichtbar – einige Maxima sind sehr lichtschwach oder fehlen komplett:

Das Interferenzmuster des Doppelspalts ist sozusagen in das Einzelspalt-Interferenzmuster eingebettet.

Aus dem Beugungsbild lässt sich die Spaltbreite ermitteln

Mit Hilfe der o.g. Überlegungen ist es nun möglich, aus dem Beugungsbild die Spaltbreite zu ermitteln – vorausgesetzt die Wellenlänge des verwendeten Lichts ist bekannt.

Der Winkel α lässt sich wie beim Doppelspalt oder optischen Gitter durch den Zusammenhang

$\tan\alpha_{k}=\dfrac {d_{k}}{a}$

ermitteln.

Stellt man den o.g. Zusammenhang – $sin\alpha_{k}=\dfrac {k\lambda}{l}$ – nach $l$ (Spaltbreite) um und setzt den Winkel dort ein, lässt sich die Spaltbreite berechnen.

Beispiel:

Der Abstand zwischen Spalt und Schirm betrage a = 2,50m, der Abstand der Maxima bzw. Minima sei d = 3,2cm. Die Wellenlänge des verwendeten Lasers betrage λ = 633nm.

Es gilt: $\tan\alpha_{k}=\dfrac {0,032m}{2,50m}=0,128$

Damit beträgt der Winkel $\alpha=0,73^{\circ}$

Bei einem so kleinen Winkel gilt mit sehr guter Näherung die Vereinfachung

$sin\alpha=tan\alpha$

Wir hätten also auch beide Gleichungen gleichsetzen können:

$\dfrac {\lambda}{l}=\dfrac {d}{a}$

Umstellen nach l liefert für die Spaltbreite

$l=\dfrac {\lambda\cdot a}{d}$

Werte einsetzen:

$l=\dfrac {6,33\cdot 10^{-7}m\cdot 2,50m}{0,032m}=4,95\cdot 10^{-5}m\simeq 0,05mm$

Ergebnis:

Die Breite des Spaltes beträgt etwa 0,05mm.

Wie sieht das Beugungsbild einer Lochblende aus?

Aus dem Beugungsbild eines Einzelspaltes kann man auch das Beugungsbild einer kreisförmigen Öffnung (Lochblende bzw. Kreisblende) vorhersagen – ist die Öffnung nicht nur zu zwei Seiten sondern zu allen Seiten gleichermaßen begrenzt, muss das Interferenzmuster symmetrisch, also zu allen Seiten gleich, aussehen.

Das Beugungsbild einer kreisförmigen Lochblende zeigt konzentrische Kreise aus Maxima und Minima:

^{Beugungsbild einer Lochblende}

In der Mitte entsteht ein Maximum, da alle Teilstrahlen mit dem gleichen Abstand zur Lochmitte bis dort den gleichen Weg zurücklegen, wodurch der Gangunterschied der Teilstrahlen 0 ist.

Aus dem Abstand der Maxima kann man wie beim Einzelspalt auf die Größe (den Durchmesser) der Lochblende schließen:

Beim Einzelspalt gilt (s.o.): $l=\dfrac {\lambda\cdot a}{d}$

Die Berechnung bei einer Kreisblende ist jedoch deutlich komplizierter, u.a. weil die Elementarwellen nicht alle die gleiche Intensität haben. Sie gelang zuerst dem französischen Physiker Augustin Jean Fresnel (1788-1827).

Letztendlich unterscheidet sich die Formel zur Berechnung des Winkels zum ersten Beugungsminimum bei einer Kreisblende von der beim Einzelspalt nur um den Faktor von ca. 1,22:

Für den Winkel $\alpha$ zum ersten Beugungsminimum an einer kreisförmigen Öffnung gilt:

$sin\, \alpha \approx 1,22\cdot \dfrac {\lambda}{l}$ bzw. für kleine Winkel $\alpha \approx 1,22\cdot \dfrac {\lambda}{l}$

wobei l hier dem Durchmesser der Lochblende entspricht.

Kreisförmige Öffnungen spielen u.a. für das Auflösungsvermögen optischer Instrumente eine bedeutende Rolle. So entspricht der Winkel $\alpha$ in der obigen Gleichung z.B. dem Winkelabstand zweier Punkte, die mit einem Fernrohr gerade noch getrennt werden können.

Das Babinetsche Prinzip – komplementäre Blenden zeigen die gleichen Beugungsbilder

Unter einer komplementären Blende versteht man eine Blende, die zu einer anderen an genau den gegensätzlichen Stellen durchlässig bzw. undurchlässig ist.

Die komplementäre Blende zu einem schmalen Spalt wäre also eine dünne Linie auf einer durchlässigen Blende oder ein dünner Draht; die komplementäre Blende zu einer Lochblende wäre ein kleiner Kreis mit dem Durchmesser der Lochblende:

^{Spaltblende und Lochblenden (unten) sowie die dazu komplementären Blenden (oben)}

Vergleicht man die Beugungsbilder derartiger Blenden mit den komplementären Blenden, so fällt kaum ein Unterschied auf:

^{Beugungsbild eines schmalen Spalts}

^{Beugungsbild einer dünnen Linie}

Das sogenannte Babinetsche Prinzip (oder auch Babinetsches Theorem) ist ein Satz aus der Optik, der besagt, dass das Beugungsbild zweier komplementärer Blenden abgesehen von der geometrischen optischen Achse (nullte Beugungsordnung) auf dem Schirm identisch ist.

Die Bezeichnung geht auf den französischen Physiker Jacques Babinett (1794-1872) zurück, der das Theorem 1837 aufstellte.

Das bedeutet:

Das Beugungsbild eines dünnen Drahtes unterscheidet sich kaum von dem eines Einzelspaltes, wenn die Spaltbreite identisch mit der Dicke des Drahtes ist.

Auch das Beugungsbild eines Kreises ist nahezu identisch mit dem einer Lochblende (s.o.):

^{Beugungsbild einer Kreisscheibe}

Info: Der Poisson-Fleck

Trotz zahlreicher Experimente von Thomas Young und Augustin Jean Fresnel gab es lange Zeit Streit um die Wellennatur des Lichts.

Von historischer Bedeutung ist die Beugung des Lichts an einer lichtundurchlässigen Kreisscheibe:

Als Fresnel bei einem Wettbewerb eine Arbeit zur Wellentheorie des Lichts einreichte, glaubte Poisson, ein Mitglied aus der Jury, durch ein einfaches Gedankenexperiment die Gültigkeit der Theorie von Fresnel zu widerlegen:

Demnach müsste im Zentrum des Schattens hinter einem runden beleuchteten Gegenstand Licht nachzuweisen sein, da das Licht dort nach der Wellentheorie konstruktiv interferieren müsste. Diese Vorstellung erschien ihm aber vollkommen absurd, darum müsse die Wellentheorie falsch sein.

Kurze Zeit später konnte die Existenz eines solchen Lichtflecks jedoch tatsächlich nachgewiesen werden.

Fresnel gewann den Wettbewerb, und der Fleck wird seitdem Poisson-Fleck genannt!

Die Breite eines Drahtes oder eines Haares bzw. der Durchmesser einer kleinen Kreisscheibe lässt sich daher auf die gleiche Art aus dem Beugungsbild ermitteln wie die Spaltbreite eines Spalts oder der Durchmesser einer Lochblende!

weiter mit Spektralanalyse mit optischem Gitter

zurück