Altersbestimmung mit der Radiocarbonmethode (C14-Methode)
Die sog. C14-Methode zur Altersbestimmung organischen Substanzen beruht auf folgendem Phänomen:
Trifft die kosmische Strahlung (im Wesentlichen Sonnenwind) auf die oberste Atmosphäre, so entstehen kaskadenförmig sehr viele verschiedene Teilchen, die sogenannte sekundäre Höhenstrahlung.
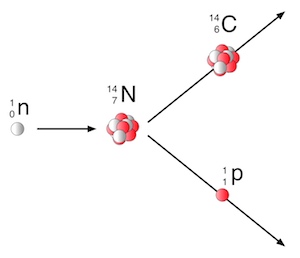Trifft nun ein Neutron der sekundären Höhenstrahlung auf ein Stickstoffatom, so geschieht manchmal die Umwandlung des Stickstoffatoms in das Kohlenstoffisotop 14C (andere Schreibweise: C14 oder C-14).
Dieses Isotop ist ein radioaktiver Betastrahler mit einer Halbwertszeit von 5730 Jahre. Es mischt sich mit den chemisch identischen und stabilen Kohlenstoffisotopen 12C und 13C.
Durch das Wettergeschehen werden die C14 – Atome gleichmäßig in der gesamten Biosphäre der Erde verteilt.
Der C14-Anteil im lebenden Organismus bleibt konstant
Durch die beschriebenen Prozesse stellen sich auf lange Sicht zwei Gleichgewichte ein:
- Ein Gleichgewicht zwischen den der Biosphäre entzogenen oder zerfallenen und den in der oberen Atmosphäre neu entstehenden Atomen
- Ein Gleichgewicht (fester Prozentsatz) zwischen 14C – und 12C – bzw. 13C – Atomen der Biosphäre
Der Anteil am gesamten Kohlenstoff in der Luft beträgt für 14C etwa 1,2·10-10 %, während 12C mit etwa 98,9% den mit Abstand größten Anteil ausmacht. Der Anteil an 13C beträgt etwa 1,1%.
Durch die Fotosynthese wird der in der Luft als CO2 vorkommende radioaktive Kohlenstoff überall im natürlichen Gleichgewichts-Verhältnis als Kohlenwasserstoff in die lebende Pflanze eingebaut und gelangt so in die gesamte Nahrungskette, also auch in den Körper von Tieren und Menschen. Der C14 – Gehalt von lebenden Pflanzen und Tieren ist damit weitgehend konstant.
Stirbt eine Pflanze, ein Tier oder ein Mensch, wird von da an kein neuer radioaktiver Kohlenstoff mehr zugeführt. Der Kohlenstoff C14 baut sich mit einer Halbwertszeit von tH = 5730 Jahren ab, der andere Kohlenstoff baut sich nicht ab. Da mit der Abnahme des C14 – Anteils immer weniger Kerne zerfallen, nimmt die Aktivität des toten Organismus mit der Zeit ab.
Findet man einen Gegenstand wie ein Holzstück, Knochen, Mumie oder Muschel, lässt sich durch Isolieren des Kohlenstoffs und Bestimmung der Aktivität das Alter der Probe bestimmen.
Weitere umfangreiche Informationen zur Radiocarbonmethode findest Du auf der Seite von chemie.de.
Rechenbeispiel zur C14-Methode
In einem Gramm Kohlenstoff aus frisch geschlagenem Holz werden 16 Zerfälle pro Minute registriert. Misst man nun in einem Gramm Kohlenstoff einer alten Probe nur 5 Zerfälle pro Minute, hat die Aktivität auf 5/16 abgenommen.
Aus der Abnahme der Aktivität und der Halbwertszeit von 14C lässt sich die Zeit berechnen, die zu dieser Abnahme geführt hat:
Es ist 
bzw. 
Für die Aktivität nach der Zeit t gilt analog zum Zerfallsgesetz
Damit gilt für dieses Beispiel:
(s.o.)
Logarithmieren ergibt
bzw. 
Umgestellt nach t erhält man
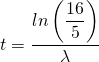
Mit 
ergibt sich für die gesuchte Zeit
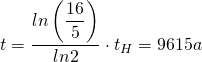
Die Probe ist also etwa 9615 Jahre alt.
Eine andere Methode zur Bestimmung des Anteils von 14C am Gesamtkohlenstoffgehalt ist die Bestimmung der Anzahl an 14C – Atomen mit Hilfe eines Massenspektrographs. Ein Vergleich mit einer (frischen) Vergleichsprobe lässt auf das Alter der Probe schließen.