Relativität der Gleichzeitigkeit

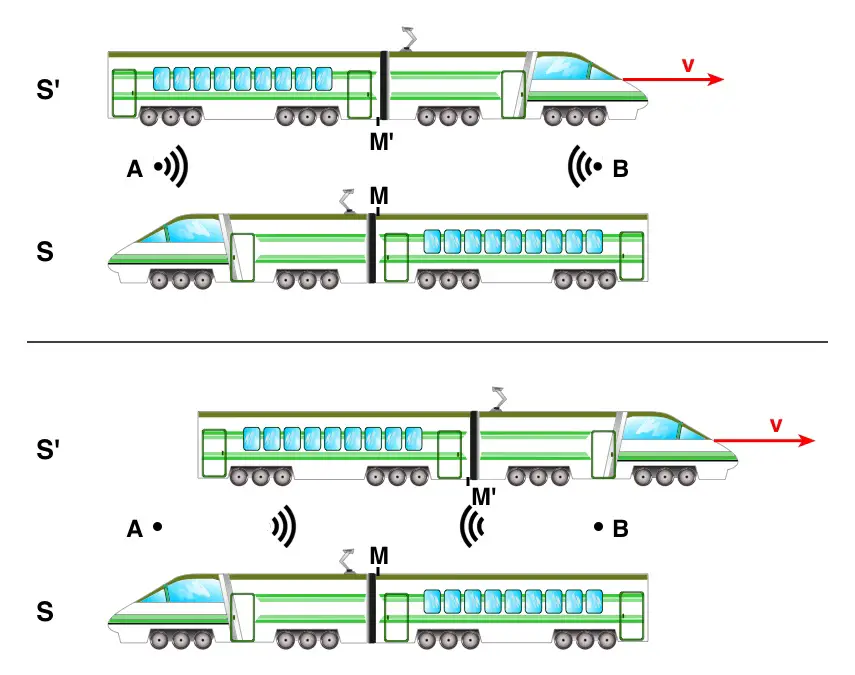
Was bedeutet Gleichzeitigkeit?

Wie wir anhand der Lorentz-Transformation nachgewiesen haben, können wir die Zeit nicht länger als absolute Größe ansehen.

Auf die Frage, ob zwei Ereignisse gleichzeitig stattfinden, ist es leicht, eine Antwort zu finden, wenn die Ereignisse am gleichen Ort stattfinden. Doch wenn die Ereignisse an verschiedenen weit voneinander entfernten Orten stattfinden, ist es viel schwieriger, eine Aussage zu treffen, weil wir die Zeit, die das Licht zu uns braucht, mit einrechnen müssen.

Da das Licht eine endliche Geschwindigkeit hat, bedeutet die gleichzeitige Beobachtung zweier Ereignisse nicht, dass diese auch gleichzeitig stattgefunden haben müssen – denn das eine Ereignis könnte viel weiter vom Beobachter entfernt stattgefunden haben als das andere.

Zur Definition der Gleichzeitigkeit eignet sich folgendes Gedankenexperiment:

An den Orten A und B schlagen gleichzeitig zwei Blitze ein:

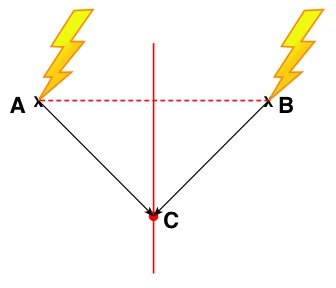
Befindet sich ein Beobachter C im gleichen Abstand zwischen den beiden Orten A und B, so registriert er die beiden Ereignisse zum gleichen Zeitpunkt, weil die Laufzeiten für das Licht jeweils gleich groß sind.

Das gilt ebenso für alle Punkte auf der roten Linie, die sich im gleichen Abstand von den beiden Orten A und B befinden.

Man kann Gleichzeitigkeit deshalb folgendermaßen definieren:

Synchronisation von Uhren

Das o.g. Gedankenexperiment lässt sich auch für die Synchronisation von Uhren verwenden, indem man an den Orten A und B jeweils eine Uhr platziert und von einem Punkt auf der roten Linie, auf der sich Punkt C befindet, ein Lichtsignal ausgesendet wird.

Es gilt:

Zwei Uhren an verschiedenen Orten werden synchronisiert, indem von ihrer geometrischen Mitte ein Lichtsignal ausgesendet wird und bei der Ankunft dieses Signals die beiden Uhren gestartet werden.

Frage:

Wenn zwei Ereignisse für einen Beobachter in einem Bezugssystem gleichzeitig stattfinden, sind sie dann auch für einen Beobachter in einem anderen relativ dazu bewegten Bezugssystem gleichzeitig?

Gedankenexperiment zur Gleichzeitigkeit zweier Ereignisse

Wir betrachten die Bewegung eines langen Zuges (System S’), der sich längs gegenüber einem anderen Zug (System S) mit hoher Geschwindigkeit in x-Richtung (nach rechts) bewegt:

Von den Punkten A und B wird gleichzeitig ein Lichtblitz ausgesendet, und zwar in dem Moment, in dem sich M und M’ genau am gleichen Ort x befinden (oberes Bild).

Das untere Bild zeigt die Situation zu einem späteren Zeitpunkt – System S’ hat sich inzwischen um die Strecke nach rechts bewegt, und die beiden Lichtblitze haben sich um die Strecke ausgebreitet.

Der Beobachter in System S in Punkt M sieht:

• Der Lichtblitz von B erreicht M’ in S’ früher als der Lichtblitz von A.
• Der Beobachter in M registriert zu einem späteren Zeitpunkt beide Blitze gleichzeitig.

Aus Sicht des Beobachters in System S’ stellt sich der Sachverhalt genau umgekehrt dar:

Der Beobachter in System S’ in Punkt M’ sieht:

• Der Lichtblitz von A erreicht M in S früher als der Lichtblitz von B.
• Der Beobachter in M’ registriert zu einem späteren Zeitpunkt beide Blitze gleichzeitig.

Aufgrund des Relativitätsprinzips können wir genauso davon ausgehen, dass sich System S’ in Ruhe befindet und sich System S mit der gleichen Geschwindigkeit v nach links bewegt. Die o.g. Aussagen aus der Sicht des Beobachters in System S’ lassen sich leicht nachvollziehen, wenn man die Abbildung entsprechend anders herum zeichnet.

Relativität der Gleichzeitigkeit

Wir sehen also, dass zwei Ereignisse, die für einen Beobachter gleichzeitig stattfinden, für einen anderen Beobachter nicht notwendigerweise gleichzeitig sein müssen. Somit ist die Gleichzeitigkeit kein absolutes Konzept!

Man mag vielleicht die Frage stellen: “Wer hat denn nun recht?”

Doch die Antwort der Relativitätstheorie lautet: Beide haben recht! Es gibt kein “bestes” Bezugssystem, von dem aus wir beurteilen könnten, welche Ansicht richtig ist. Beide Ansichten sind absolut gleichberechtigt.

Dass wir im Alltag nichts davon bemerken, dass die Gleichzeitigkeit kein absolutes Konzept ist, liegt daran, dass sich der hier beschriebene Effekt nur bemerkbar macht, wenn die Relativgeschwindigkeit zwischen den beiden Bezugssystemen sehr groß (in der Nähe von c) ist oder die Entfernungen sehr groß sind.

Führt man diese Überlegungen weiter, so erkennt man, dass auch die Zeitdauer eines Vorgangs vom Bezugssystem abhängt.