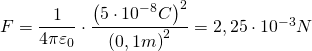Feldstärke und Kraftwirkung im Radialfeld
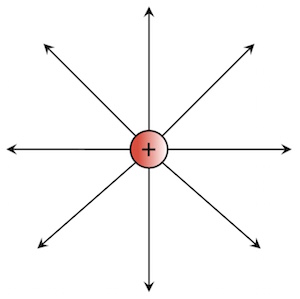
Homogene Felder zeichnen sich dadurch aus, dass die Feldstärke überall gleich groß ist. Es gibt jedoch auch Feldformen, in denen dies nicht der Fall ist. Ein solches Feld kennen wir schon, nämlich das Feld um eine punktförmige Ladung bzw. um eine geladene Kugel herum:
Ein solches Feld bezeichnet man als Radialfeld.
Letztendlich kann man sich alle anderen Feldlinienbilder aus Radialfeldern zusammengesetzt vorstellen.
Die Feldstärke im Radialfeld lässt sich aus der Dichte der Feldlinien ableiten.
Offensichtlich gilt im Radialfeld:
Die Feldstärke nimmt im Radialfeld mit zunehmendem Abstand ab.
Folgende Fragen sollen nun geklärt werden:
- Wie hängt die elektrische Feldstärke vom Abstand zur Ladung bzw. vom Abstand zum Kugelmittelpunkt einer geladenen Kugel ab?
- Hängt die elektrische Feldstärke an einem bestimmten Ort von der Kugeloberfläche bzw. vom Kugelradius ab? (Anders gefragt: Macht es einen Unterschied, wie groß die Kugel bei gleicher Ladung q ist?)
Das Coulomb’sche Gesetz
Um die o.g. Fragen zu klären, wird folgender Versuch durchgeführt:
Versuch:
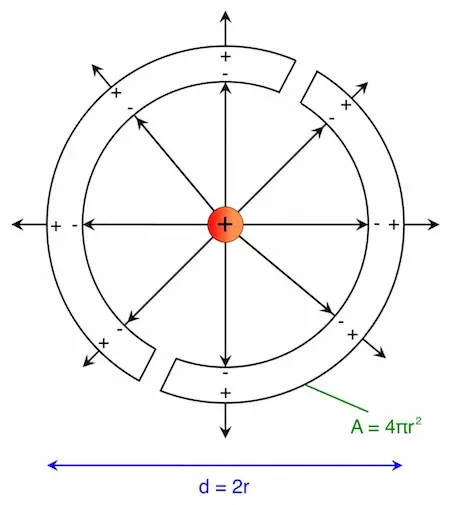
In die Nähe einer geladenen Metallkugel wird ein Probekörper mit einer kleinen Ladung q gebracht, der im elektrischen Feld ausgelenkt wird. Die Auslenkung hängt dabei von der Feldstärke ab.
(Wenn man die Feldstärke durch Veränderung der Ladung Q auf der Kugel ändert, so ändert sich auch die Auslenkung.)
Um die geladene Kugel werden zwei Halbkugelschalen mit dem Radius r gelegt.
Beobachtung:
Die Auslenkung des Probekörpers ändert sich nicht. Das bedeutet, dass sich die Feldstarke am Ort der Probeladung nicht verändert hat.
Durch Influenz kommt es auf den Kugelschalen zur Ladungstrennung: