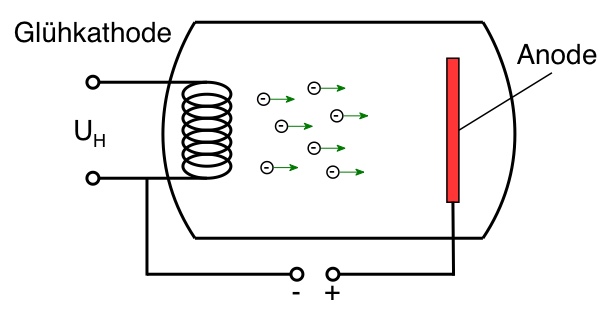
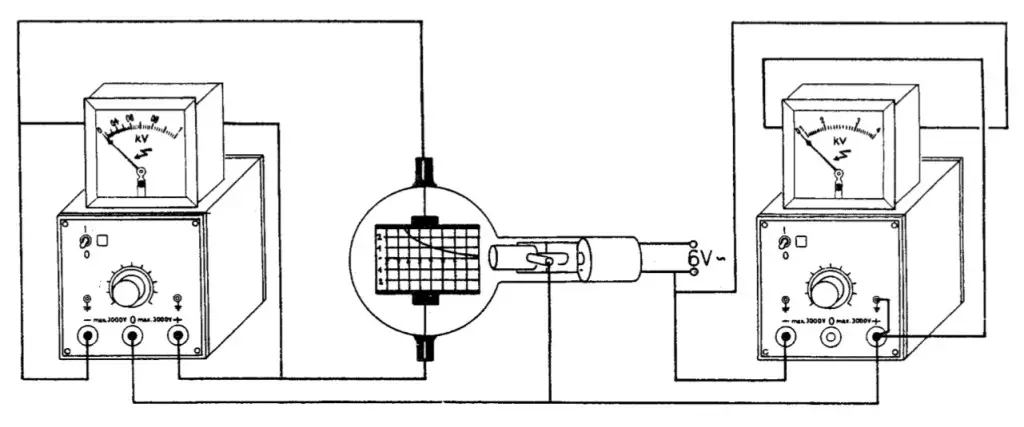
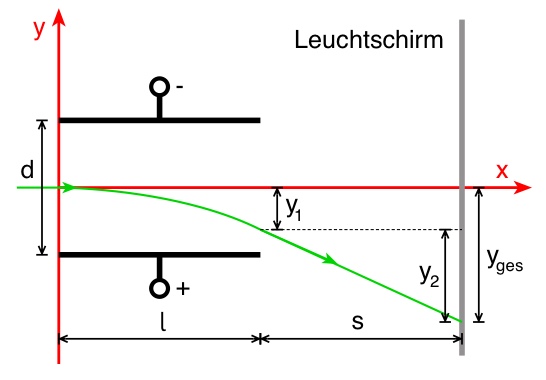
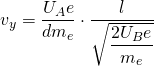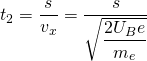Elektronen im elektrischen Feld - Ablenkung von Elektronen im Querfeld

Wie verhalten sich Elektronen in einem elektrischen Feld?

Befindet sich ein Elektron in einem elektrischen Feld, so erfährt es eine Kraft, und zwar die Kraft $F_{el} = E\cdot q$ , wobei die Ladung $q$ der Ladung eines Elektrons, der Elementarladung $e$ , entspricht.

Die Kraft auf ein Elektron in einem elektrischen Feld ist also nur von der elektrischen Feldstärke $E$ abhängig und beträgt bei einer Feldstärke von $E=1N/C$ :

$F=E\cdot e=1\dfrac {N}{C}\cdot 1,602\cdot 10^{-19}C=1,602\cdot 10^{-19}N$

Diese Kraft bewirkt eine Beschleunigung des Elektrons (es gilt: $F=m\cdot a$ ).

Ist die Kraft konstant (was in einem homogenen Feld der Fall ist), ist auch die Beschleunigung konstant.

Das Elektron erhält also kinetische Energie. Die Energie stammt aus dem elektrischen Feld (die Energie des elektrischen Feldes beträgt: $E_{el}= U\cdot Q$ bzw. $E_{el}= U\cdot e$ ).

Die Energie, die ein Elektron in einem homogenen Feld erhält, beträgt

$E_{el}=U\cdot e$

Die elektrische Energie wird beim Durchlaufen der Spannung $U$ in kinetische Energie umgewandelt.

Die kinetische Energie eines Elektrons, welches durch eine Spannung von $U=1V$ beschleunigt wurde, beträgt

$E_{kin}=E_{el}=U\cdot e=1V\cdot 1,602\cdot 10^{-19}C=1,602\cdot 10^{-19}J$

(Zur Erinnerung: $1V=1\frac {J}{C})$

Die Energie von Elektronen wird in Elektronenvolt angegeben

Der Energiebetrag in der Einheit Joule ist für einzelne Elektronen selbst bei hohen Spannungen sehr klein. Aus diesem Grund ist für die Energie von Elektronen eine andere Einheit gebräuchlich:

Man setzt den entsprechenden Wert für die Elementarladung in der obigen Gleichung $E=U\cdot e$ nicht ein, sondern lässt das Symbol für die Elementarladung als “ $e$ ” stehen.

Damit ergibt sich als Energieeinheit das Elektronenvolt (eV).

Das hat zwei Vorteile:

Man kommt ohne 10er-Potenzen mit negativem Exponenten aus.
Die Energie hat in der Einheit Elektronenvolt den gleichen Zahlenwert wie die durchlaufende Spannung.

Beispiel:

Ein Elektron durchläuft eine Spannung von $U=500V$ .

Die Energie, die es dadurch erhält, beträgt $E=500V\cdot e=500eV$ (Elektronenvolt)

Energieeinheit Elektronenvolt

1 Elektronenvolt ist die Energie, die ein Teilchen mit der Ladung 1e (der Elementarladung) erhält, wenn es eine Spannung von 1V durchläuft.

Damit gilt: 1 eV = 1,602 · 10^-19 C · 1V = 1,602 · 10^-19 J

(1CV = 1J)

Wird eine elektrische Spannung dafür verwendet, ein geladenes Teilchen zu beschleunigen, wird die Spannung als Beschleunigungsspannung U_B bezeichnet.

Durchläuft ein Elektron eine Beschleunigungsspannung U_B, wird die elektrische Energie vollständig in kinetische Energie umgewandelt.

Mit dem Ansatz der Energieerhaltung lässt sich eine Formel für die Geschwindigkeit von Elektronen herleiten, die in einem elektrischen Feld beschleunigt wurden:

Es gilt:

$E_{kin}=E_{el}$

und damit

$\frac {1}{2}mv^{2}=U_{B}\cdot E$

Stellt man diese Gleichung nach $v$ um, erhält man:

$v=\sqrt {\dfrac {2 U_{B}\cdot e}{m_{e}}}$

Darin ist $m_{e}$ die Masse eines Elektrons. Ist diese bekannt, lässt sich so die Geschwindigkeit der im elektrischen Feld beschleunigten Elektronen berechnen.

Die Elektronenmasse wurde bisher nicht ermittelt, sie lässt sich aber in der Formelsammlung nachschlagen.

Vielleicht lässt sich ja die Elektronenmasse durch die Untersuchung beschleunigter Elektron im elektrischen Feld bestimmen?

Um diese Frage zu klären, soll das Verhalten von Elektronen im elektrischen Feld genauer untersucht werden.

Wie erzeugt man freie Elektronen?

Um Elektronen im elektrischen Feld untersuchen zu können, muss man zunächst freie Elektronen erzeugen, also Elektronen, die nicht an einen Leiter gebunden sind.

Glühelektrischer Effekt

Der sogenannte glühelektrische Effekt wurde im Jahre 1883 von Thomas Alva Edison entdeckt:

Aus der erhitzten Oberfläche eines Metalls treten im Vakuum Elektronen aus.

Durch die Erhitzung erhalten locker sitzende Elektronen an der Oberfläche genügend kinetische Energie, um das Metall zu verlassen.

Für die Erzeugung freier Elektronen benutzt man eine Hochvakuum-Diode.

Schematischer Aufbau einer Hochvakuum-Diode

Hochvakuum-Diode Glühelektrischer Effekt

Durch die Heizung (Heizspannung $U_{H}$ lösen sich die Elektronen aus der Metalloberfläche der Glühlathode und werden durch die angelegte Spannung zwischen Glühkathode und Andode zur Anode hin beschleunigt.

Die Elektronen sind unsichtbar, aber durch den Stromfluss nachweisbar.

Elektronenstrahlröhre (Braunsche Röhre)

In eine Braunschen Röhre (benannt nach ihrem Erfinder Carl Ferdinand Braun im Jahre 1897) werden Elektronen zu einem Strahl gebündelt und beschleunigt und treffen auf einen Leuchtschirm. Durch horizontale und vertikale Ablenkplatten kann der Elektronenstrahl auf jeden Punkt des Schirms gelenkt werden.

Genauere Informationen zum Aufbau und zur Funktionsweise einer Braunschen Röhre findest Du bei Leifiphysik auf der Seite zu bewegten Ladungen in Feldern.

Untersuchung der Ablenkung von Elektronen im elektrischen Feld

Um das Verhalten von Elektronen im elektrischen Feld zu untersuchen, verwenden wir eine spezielle Elektronenstrahlröhre, in der sich ein Leuchtschirm befindet, der den Verlauf des Elektronenstrahls sichtbar macht.

Der Leuchtschirm ist mit einer Skalierung versehen, außerdem kann der Elektronenstrahl durch ein horizontales elektrisches Feld senkrecht zur Bewegungsrichtung der Elektronen abgelenkt werden:

Elektronenstrahlröhre_u2

Folgende Abbildung zeigt den vollständigen Versuchsaufbau:

Die Elektronen werden zunächst durch die Beschleunigungsspannung U_B beschleunigt.

Die Bahn der Elektronen wird durch den Leuchtschirm sichtbar gemacht. Durch die Spannung zwischen den horizontalen Platten werden die Elektronen abgelenkt. Daher wird diese Spannung als Ablenkspannung U_A bezeichnet.

Wie sieht die Bahn der Elektronen aus, wenn diese in das horizontale elektrische Feld gelangen?

Die Beschleunigungsspannung wird auf einen Wert von einigen kV erhöht, anschließend wird eine Ablenkspannung (ebenfalls in der Größenordnung von einigen kV) angelegt.

Beobachtung:

Elektronenstrahlröhre_u1

Ist die untere Platte positiv geladen, wird der Elektronenstrahl nach unten abgelenkt. Die Bahn des Elektronenstrahls erinnert an die Wurfparabel bei einem horizontalen Wurf.

Bei entgegengesetzter Ablenkspannung (obere Platte positiv), wird der Elektronenstrahl nach oben abgelenkt.

Wie kommt diese Bahn zustande?

Zur Erklärung der Elektronenbahn erinnern wir uns zunächst an die Erklärung der Wurfparabel bei einem horizontalen Wurf:

Analogie zum waagerechten Wurf:

Beim waagerechten Wurf kommt es zur Überlagerung von zwei Teilbewegungen:

In x-Richtung: gleichförmige Bewegung (v_x bleibt konstant)

In y-Richtung: gleichmäßig beschleunigte Bewegung (v_y wird größer)

Beim horizontalen Wurf beträgt die Beschleunigung in y-Richtung a_y = g

Die Bewegungsgleichungen lauten

für den Weg in x-Richtung: $x=v_{x}t$

für den Weg in y-Richtung: $y=\frac {1}{2}gt^{2}$

$t$ bzw. $t^{2}$ lässt sich mit der oberen Gleichung ersetzen:

$t^{2}=\dfrac {x^{2}}{v_{x}^{2}}$

Damit ergibt sich die Bahngleichung für den horizontalen Wurf:

$y=\dfrac {1}{2}g\dfrac {x^{2}}{v_{x}^{2}}$

Erklärung der Elektronenbahn

Auch in diesem Versuch kommt es zu einer Überlagerung zweier Teilbewegungen:

1. Nach Durchlaufen der Beschleunigungsspannung bewegen sich die Elektronen gleichförmig in x-Richtung.
2. Aufgrund der konstanten Kraft im horizontalen elektrischen Feld erfolgt in y-Richtung eine gleichmäßige Beschleunigung.

Hinweis:

Es wirkt zwar zusätzlich auch die Gewichtskraft auf die Elektronen, diese ist jedoch um den Faktor 10¹⁴(!) kleiner als die elektrische Kraft und kann daher vernachlässigt werden.

Das lässt sich leicht überprüfen – ohne Anlegen einer Ablenkspannung verläuft der Elektronenstrahl waagerecht.

Es sollte also möglich sein, die Bewegungsgleichung für die Elektronenbahn mit den gleichen Überlegungen herzuleiten wie für die Bahn beim horizontalen Wurf.

Dazu muss nur die Gewichtskraft als beschleunigende Kraft in y-Richtung durch die elektrische Kraft ersetzt werden:

$F_{el}=E\cdot e$

Mit Hilfe der Grundgleichung der Mechanik [ $F=ma$ ] ergibt sich für die Beschleunigung

$a_{y}=\dfrac {F_{el}}{m_{e}}$

Setzt man dies in die Bewegungsgleichung für den waagerechten Wurf (s.o.) ein, erhält man

$y=\dfrac {1}{2}a_{y}\dfrac {x^{2}}{v_{x}^{2}}$ bzw. $y=\dfrac {1}{2}\dfrac {F_{el}}{m_{e}}\dfrac {x^{2}}{v_{x}^{2}}$

Für die Kraft im elektrischen Feld auf ein Elektron gilt:

$F_{el}=E\cdot e$ (analog gilt im Gravitaionsfeld: $F_{G}=mg$ )

Für die Beschleunigung in y-Richtung gilt also

$a_{y}=\dfrac {E\cdot e}{m_{e}}$

Damit kann man für die Ablenkung in y-Richtung schreiben:

$y=\dfrac {1}{2}\dfrac {E\cdot e\cdot x^{2}}{m_{e}\cdot v_{x}^{2}}$ (1)

Aufstellen der Bewegungsgleichung

Nun soll eine Bewegungsgleichung in der Form y(x)=… aufgestellt werden, die nur Größen enthält, die wir bestimmen können oder schon kennen.

Gemessen werden können die Größen U_A, U_B, und d.

Die elektrische Feldstärke E kann außerdem mit $E=\dfrac {U}{d}$ berechnet werden, e ist bekannt.

Darüber hinaus gilt für die Geschwindigkeit in x-Richtung der Zusammenhang

$v_{x}=\sqrt {2\dfrac {e}{m_{e}}U_{B}}$ (s.o.)

Quadriert man diese Gleichung, erhält man

$v_{x}^{2}=2\dfrac {e}{m_{e}}U_{B}$

Diesen Ausdruck für v_x² kann man in die zuvor aufgestellte Gleichung (1) einsetzen. Damit ergibt sich:

$y=\dfrac {1}{2}\dfrac {U_{A}e}{dm_{e}}\cdot \dfrac {x^{2}m_{e}}{2eU_{B}}$

Durch Kürzen erhält man schließlich die gesuchte Bahngleichung:

$y=\dfrac {U_{A}}{4dU_{B}}\cdot x^{2}$

Da diese Gleichung die Form $y(x)=const.\cdot \, x^{2}$ besitzt, wird die Vermutung bestätigt, dass es sich um eine Parabelbahn handelt.

Ablenkung von Elektronen im elektrischen Querfeld

Die Bahngleichung für die Ablenkung von Elektronen im elektrischen Querfeld lautet:

$y=\dfrac {U_{A}}{4dU_{B}}\cdot x^{2}$

Aus dieser Bahngleichung ergeben sich folgende Zusammenhänge:

Die Ablenkung in y-Richtung ist proportional zur Ablenkspannung U_A und umgekehrt proportional zur Beschleunigungsspannung U_B.

Es lässt sich einfach zeigen:

⇒ Je größer die Beschleunigungsspannung, umso kleiner die Ablenkung

⇒ Je größer die Ablenkspannung, umso größer die Ablenkung

Mit der aufgestellten Bewegungsgleichung ist es möglich, für jede x-Position die genaue Ablenkung bzw. die y-Position zu berechnen.

Eine experimentelle Überprüfung durch genaues Messen der Positionen des Elektronenstrahls bestätigt den hergeleiteten Zusammenhang.

Gesamtablenkung bis zu Schirm

In einer Braun’schen Röhre werden die Elektronen in einem Kondensator abgelenkt und gelangen dann auf einen weiter entfernten Schirm.

Wir wollen nun die Gesamtablenkung $y_{ges}$ bis zum Schirm berechnen.

Nach den Verlassen des Kondensators der Länge $l$ haben die Elektronen eine konstante resultierende Geschwindigkeit aus $v_{x}$ und $v_{y}$ . Sie treffen auf einen Beobachtungssschirm im Abstand $s$ .

Die Gesamtablenkung $y_{ges}$ setzt sich zusammen aus der Ablenkung innerhalb des Kondensators $y_{1}$ und der Ablenkung hinter dem Kondensator $y_{2}$ .

Es gilt also: $y_{ges}=y_{1}+y_{2}$

Elektronenablenkung Braunsche Röhre

Die Ablenkung innerhalb des Kondensators $y_{1}$ lässt sich mit Hilfe der bereits hergeleiteten Bahngleichung (s.o.) berechnen, indem man für $x$ die Kondensatorlänge $l$ einsetzt. Man erhält so

$y_{1}=\dfrac {U_{A}}{4dU_{B}}\cdot l^{2}$ bzw. $y_{1}=\dfrac {U_{A}\cdot l^{2}}{4d\cdot U_{B}}$

Berechnung der Ablenkung zwischen Kondensator und Schirm

Um die Ablenkung $y_{2}$ herzuleiten, gibt es verschiedene Wege.

Der einfachste und eleganteste Weg ist, zunächst die Steigung der Tangente an der Parabel am Punkt $x=l$ (also am Ende des Kondensators) zu bestimmen. Da hinter dem Kondensator keine weitere Ablenkung erfolgt, bleibt diese Steigung (also die Richtung des Elektronenstrahls) bis zum Schirm konstant.

Die Steigung der Tangente erhält man mit der Ableitung $y_{1}'(x)$ bzw. $y_{1}'(l)=\dfrac {U_{A}\cdot l}{2d\cdot U_{B}}$ .

Für die Ablenkung $y_{2}$ gilt dann: $y_{2}=mx$ , wobei $m$ die Steigung, also $y_{1}'(l)$ (s.o.), ist und für “ $x$ ” die Strecke $s$ eingesetzt wird.

Damit erhält man:

$y_{2}=\dfrac {U_{A}\cdot l\cdot s}{2d\cdot U_{B}}$ und $y_{ges}=y_{1}+y_{2}=\dfrac {U_{A}\cdot l^{2}}{4d\cdot U_{B}}+\dfrac {U_{A}\cdot l\cdot s}{2d\cdot U_{B}}$

Durch Ausklammern erhält man

$y_{ges}=\dfrac {U_{A}\cdot l}{2d\cdot U_{B}}\cdot \left(\dfrac {l}{2}+s\right)$ oder $y_{ges}=\dfrac {U_{A}\cdot l(l+2s)}{4d\cdot U_{B}}$

Die Gesamtablenkung der Elektronen in einer Braunschen Röhre beträgt

$y_{ges}=\dfrac {U_{A}\cdot l(l+2s)}{4d\cdot U_{B}}$

mit $l$ = Länge des Kondensators, $s$ = Abstand zwischen Kondensator und Schirm

Alternative Herleitung ohne Differentialrechnung

Die Formel für die Gesamtablenkung lässt sich auch mit Hilfe der Bewegungsgesetze für gleichförmige und gleichmäßig beschleunigte Bewegungen herleiten:

Die Zeit innerhalb des kondensators beträgt $t_{1}=\dfrac {l}{v_{x}}=\dfrac {l}{\sqrt {\dfrac {2U_{B}e}{m_{e}}}}$ (1)

Für die Ablenkung im, Kondensator $y_{1}$ gilt (s.o.):

$y_{1}=\dfrac {U_{A}\cdot l^{2}}{4d\cdot U_{B}}$

Auch diese bereits oben hergeleitete Formel ließe sich mit Hilfe der Bewegungsgleichungen herleiten:

Es gilt: $y_{1}=\frac {1}{2}a_{y}t_{1}^{2}$ mit $a_{y}=\dfrac {F_{el}}{m_{e}}=\dfrac {Ee}{m_{e}}=\dfrac {U_{A}e}{dm_{e}}$ (2)

Damit und mit (1) ergibt sich für die Ablenkung

$y_{1}=\dfrac {U_{A}e}{2dm_{e}}\cdot \dfrac {l^{2}m_{e}}{2U_{B}e}$

Es lassen sich sowohl Elektronenmasse $m_{e}$ also auch die Elementarladung $e$ kürzen. Außerdem kann man die Brüche zusammenfassen.

So erhält man schließlich die gleiche Formel für die Ablenkung im Kondensator $y_{1}$ wie oben:

$y_{1}=\dfrac {U_{A}l^{2}}{4dU_{B}}$

Berechnung von $y_{2}$ :

Für die am Ende des Kondensator erreichte vertikale Geschwindigkeit gilt:

$v_{y}=a_{y}\cdot t_{1}$

Setzt man darin die oben hergeleiteten Ausdrücke für die Zeit $t_{1}$ (1) und die Beschleunigung $a_{y}$ (2) ein, so erhält man

$v_{y}=\dfrac {U_{A}e}{dm_{e}}\cdot \dfrac {l}{\sqrt {\dfrac {2U_{B}e}{m_{e}}}}$

Für die Ablenkung zwischen Kondensator und Schirm $y_{2}$ gilt:

$y_{2}=v_{y}\cdot t_{2}$ mit $t_{2}=\dfrac {s}{v_{x}}=\dfrac {s}{\sqrt {\dfrac {2U_{B}e}{m_{e}}}}$

Damit ergibt sich

$y_{2}=\dfrac {U_{A}e}{dm_{e}}\cdot \dfrac {l}{v_{x}}\cdot {s}{v_{x}}=\dfrac {U_{A}els}{dm_{e}v_{x}^{2}}$

Setzt man darin die Geschwindigkeit $v_{x}=\sqrt {\dfrac {2U_{B}e}{m_{e}}}$ ein, so erhält man schließlich

$y_{2}=\dfrac {U_{A}ls}{2dU_{B}}$

Die Gesamtablenkung ergibt sich aus der Summe beider Ablenkungen

$y_{ges}=y_{1}+y_{2}$

$y_{ges}=\dfrac {U_{A}l^{2}}{4dU_{B}}+\dfrac {U_{A}ls}{2dU_{B}}$

Ausklammern von $\dfrac {U_{A}l}{4dU_{B}}$ führt zu

$y_{ges}=\dfrac {U_{A}\cdot l(l+2s)}{4d\cdot U_{A}}$

und damit zur gleichen Formel, die wir oben auf anderem Weg hergeleitet haben.

zurück