Interferenz an dünnen Schichten

Ist Interferenz auch ohne Beugung möglich?

Bei allen bisherigen Experimenten zur Interferenz von Licht trat Beugung auf. Doch es gibt auch Interferenz ohne Beugung.

Das farbige Schillern von Seifenblasen, Libellenflügeln oder einer dünnen Ölschicht auf Wasser entsteht ebenfalls durch Interferenz. Verantwortlich dafür ist der Umstand, dass das Licht, welches auf eine sehr dünne Schicht fällt, an der Vorder- und Rückseite dieser Schicht reflektiert wird und anschließend interferiert.

Zur Demonstration der Interferenz an dünnen Schichten wird folgender Versuch durchgeführt:

Versuch:

Vor eine Quecksilber- oder Natriumlampe wird ein dünnes Glimmerblatt (Dicke ca. 0,05mm) gehalten, so dass das reflektierte Licht auf einen Schirm bzw. auf eine Wand fällt.

Beobachtung:

Auf dem Schirm entsteht ein ringförmiges Interferenzmuster.

Erklärung:

Das Licht wird sowohl an der Vorder- als auch an der Rückseite des Glimmerblattes reflektiert und interferiert miteinander. Je nach Gangunterschied, der von verschiedenen Faktoren abhängt, kommt es zur Verstärkung oder zur Abschwächung bzw. Auslöschung.

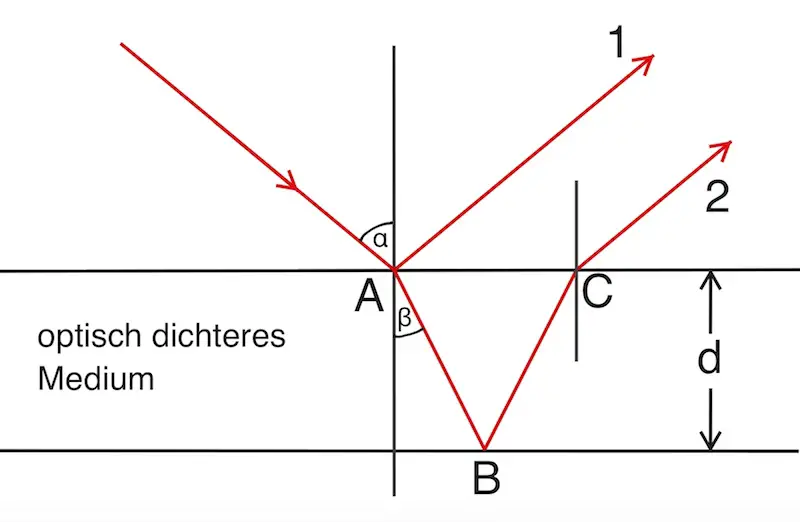
In der folgenden Skizze werden die möglichen Lichtwege der reflektierten Teilstrahlen dargestellt:

Das Licht trifft unter dem Winkel α auf die Grenzschicht zwischen Luft und Glimmerblatt (Punkt A). Dort wird eine Teil des Lichts reflektiert (Teilstrahl 1). Es gilt das Reflexionsgesetz.

Ein anderer Teil des Lichts dringt in das Glimmerblatt ein und wird erst an der Rückseite des Glimmerblattes (Punkt B) reflektiert.

Beim Eintritt in das Glimmerblatt wird das Licht gebrochen. Da das Glimmerblatt optisch dichter ist als Luft, wird das Licht zum Lot hin gebrochen (β < α).

Wenn das Licht das Glimmerblatt an der Grenzschicht zwischen Glimmerblatt und Luft (Punkt C) wieder verlässt, wird es erneut gebrochen, diesmal vom Lot weg.

Teilstrahl 2 verlässt das Glimmerblatt unter dem gleichen Winkel wie Teilstrahl 1 – beide Teilstrahlen sind also parallel.

Da die Schichtdicke d in Wirklichkeit sehr klein ist, treffen Teilstrahl 1 und Teilstrahl 2 praktisch am selben Punkt auf den Schirm bzw. ins Auge und interferieren miteinander.

Wann ensteht konstruktive, wann destruktive Interferenz?

Ob die beiden Teilstrahlen konstruktiv oder destruktiv miteinander interferieren, hängt vom Gangunterschied δ ab.

Die beiden Teilstrahlen 1 und 2 haben aus verschiedenen Gründen einen Gangunterschied:

Die beiden Strahlen 1 und 2 legen verschieden lange Wege zurück

Bei der Reflexion tritt unter Umständen* ein Phasensprung auf

Der Umweg von Strahl 2 führt zum Teil durch das Glimmerblatt. Dort hat das Licht eine kleinere Wellenlänge (und Ausbreitungsgeschwindigkeit) als in Luft

* Von mechanischen Wellen wissen wir, dass bei der Reflexion am festen Ende ein Phasensprung von 180° bzw. λ/2 auftritt, bei der Reflexion am freien Ende gibt es jedoch keinen Phasensprung.

Ermittlung des Gangunterschiedes

Um den Gangunterschied zu ermitteln, betrachten wir nacheinander alle genannten Gründe. Der Einfachheit halber beschränken wir uns zunächst auf den Spezialfall, dass das Licht senkrecht auf die Grenzfläche trifft.

1. Geometrische Weglänge

Bei senkrechten Einfall muss Teilstrahl 2 gegenüber Teilstrahl 1 zusätzlich die Schicht zweimal durchlaufen. Der geometrische Wegunterschied beträgt also $\Delta s=2d$ .

2. Optische Weglänge – Änderung der Wellenlänge im Glimmerblatt

Da sich das Licht im Glimmerblatt um den Faktor $n$ (= Brechungszahl) langsamer ausbreitet als in Luft, verringert sich die Wellenlänge um den gleichen Faktor.

Die Wellenlänge im Glimmerblatt beträgt also nicht $\lambda$ , sondern $\dfrac {\lambda}{n}$ .

Der Gangunterschied wird entsprechend um den Faktor $n$ größer.

Der Gangunterschied unter Berücksichtigung der Brechung beträgt beim senkrechten Einfall also

$\delta=2dn$

Man spricht hierbei auch von optischer Weglänge.

Wie wir wissen, kommt es zur Auslöschung, wenn der Gangunterschied einem ungeradzahligen Vielfachen der halben Wellenlänge entspricht:

$\delta=(2k+1)\dfrac {\lambda}{2}$ Bedingung für Auslöschung

Demnach müsste für die Auslöschung gelten: $2dn=(2k+1)\dfrac {\lambda}{2}$

Allerdings gibt es einen weiteren Grund für einen Gangunterschied:

3. Phasensprung durch Reflexion

Bei der Reflexion des Lichts am optisch dichteren Medium (Punkt A) kommt es zu einem Phasensprung von 180° bzw. λ/2. Das bedeutet: Aus einem Wellenberg wird ein Wellental und umgekehrt.

Bei der Reflexion am optisch dünneren Medium (Punkt B) gibt es keinen Phasensprung.

Da der Phasensprung also nur bei einem der beiden Teilstrahlen auftritt, kommt zusätzlich zum o.g. Gangunterschied noch eine Phasenverschiebung um λ/2 hinzu.

Der gesamte Gangunterschied beträgt damit:

$\delta=2dn+\dfrac {\lambda}{2}$

Damit lautet die Bedingung für Auslöschung:

$2dn+\dfrac {\lambda}{2}=(2k+1)\dfrac {\lambda}{2}$

Nach Auflösen der Klammer und anschließendem Kürzen ergibt sich:

$2dn=k\lambda$

Die Bedingung für Verstärkung lautet

$2dn=\dfrac {2k-1}{2}\cdot \lambda$ mit k = 1, 2, 3, …

Interferenz an dünnen Schichten

Trifft Licht senkrecht auf eine dünne planparallele Schicht, tritt bei der Reflexion unter folgenden Bedingungen Auslöschung bzw. maximale Verstärkung auf:

Bedingung für Auslöschung:

$2dn=k\lambda$

Bedingung für maximale Verstärkung:

$2dn=\dfrac {2k-1}{2}\cdot \lambda$

mit k = 1, 2, 3, …

Bei nicht senkrechtem Einfall ist die Herleitung etwas komplizierter.

Trifft das Licht unter einem Winkel α auf die Grenzfläche, so beträgt der zusätzliche Lichtweg (die zusätzliche optische Weglänge)

$\delta=2d\sqrt {n^{2}-sin^{2}\alpha}$

Der gesamte Gangunterschied unter Berücksichtung des Phasensprungs von Teilstrahl 1 beträgt damit

$\delta=2d\sqrt {n^{2}-sin^{2}\alpha}+\dfrac {\lambda}{2}$

Daraus ergeben sich folgende Bedingungen für Auslöschung bzw. Verstärkung:

Bedingung für Auslöschung:

$\delta=2d\sqrt {n^{2}-sin^{2}\alpha}=k\lambda$

Bedingung für maximale Verstärkung:

$\delta=2d\sqrt {n^{2}-sin^{2}\alpha}=\dfrac {2k-1}{2}\cdot \lambda$

Ob an einer bestimmten Stelle ein Maximum oder ein Minimum entsteht, hängt also vom Winkel (und damit vom Ort auf dem Schirm) und von der Schichtdicke ab.

Info: Die Herleitung sowie weitere Informationen findest Du unter Lernhelfer / Schülerlexikon

Warum tritt dieser Effekt nur bei sehr dünnen Schichten auf?

Der Grund, warum diese Form der Interferenz nur bei sehr dünnen Schichten auftritt, ist die Kohärenzlänge von Licht. Wie hier beschrieben, ist die Kohärenzlänge des Lichts von gewöhnlichen Lichtquellen sehr kurz.

Der Gangunterschied ist umso größer, je dicker die Schicht ist. Ist der Gangunterschied jedoch größer als die Kohärenzlänge des einfallenden Lichts, dann gibt es zwischen den beiden Teilstrahlen keine feste Phasenbeziehung mehr, demzufolge kann kein stabiles Interferenzmuster entstehen.

Mit einem Laser, dessen Licht sehr kohärent ist, tritt dieser Effekt auch bei dickeren Schichten, wie z.B. einer Glasscheibe, auf. Allerdings muss man dazu das Licht des Lasers mit einer Zerstreuungslinse aufweiten, damit das Licht auf eine größere Fläche treffen kann.

Bekannte Phänomene von Interferenz an dünnen Schichten

Auch wenn den meisten das Entstehen dieser Phänomene unbekannt ist, so haben sie doch alle schon einmal beobachtet:

Seifenblasen schimmern farbig, da das Licht auf die dünne Seifenhaut fällt, die das Licht teilweise durchlässt und reflektiert. Die Reflexion findet sowohl an der Außen- als auch an der Innenseite der Seifenblase statt. Je nach Schichtdicke und Blickwinkel interferieren die verschiedenen Lichtfarben des an den beiden Grenzschichten reflektierten Lichts entweder konstruktiv oder destruktiv. Was wir sehen, ist die Mischung aus den Lichtfarben, die nicht ausgelöscht werden. Es handelt sich dabei um die Komplementärfarbe des ausgelöschten Lichts.

Da eine Seifenblase meist nicht stillsteht, so dass sich der Betrachtungswinkel ständig ändert und zudem die Seifenhaut durch die Schwerkraft nach unten läuft und so unten dicker wird, bis sie oben schließlich so dünn wird, dass die Seifenblase platzt, ändert sich der Farbverlauf ständig. Das erzeugt den Eindruck des “Schillerns”.

Ein Ölfleck z.B. auf einer Pfütze oder direkt auf der Straße bildet ebenfalls eine sehr dünne Schicht. Der Effekt ist praktisch der gleiche wie bei Seifenblasen. Je nach Dicke der Ölschicht und Blickwinkel werden bestimmte Farben im reflektierten Licht ausgelöscht.

Auch bei Newtonschen Ringen handelt es sich um eine auch im Alltag beobachtbare Erscheinung. Newtonsche Ringe entstehen durch die Interferenz des Lichts, das an der oberen und an der unteren Grenzfläche eines Luftkeils zwischen zwei nahezu parallelen Oberflächen reflektiert wird. Sie lassen sich gezielt erzeugen, indem man eine Plankonvexlinse mit großem Krümmungsradius mit der gekrümmten Seite auf eine Glasplatte legt und mit Licht bescheint. Durch die von der Mitte nach außen hin dicker werdende Luftschicht zwischen Glasplatte und Linse entstehen bei weißem Licht farbige Ringe.

Liegen zwei planparallele Glasplatten (z.B. zwei Objektträger zum Mikroskopieren) aufeinander, bildet sich meist auch eine sehr dünne Luftschicht, die durch Zusammendrücken der Glasplatten kleiner wird. Auch hier sind Farbverläufe zu erkennen, die dann nicht wie Ringe sondern eher wie Streifen aussehen.

Legt man ein sehr dünnes Objekt, z.B. ein Haare, zwischen die Objektträger, so entstehen parallele farbige Streifen, weil die Luftschicht zwischen den Glasplatten einen Keil bildet. Man kann so durch Abzählen der Streifen die Dicke des Haares bestimmen.

Das Phänomen von Interferenz an dünnen Schichten kann man sich auch für die Entspiegelung von Oberflächen, wie z.B. Brillengläser oder auch Displays, nutzbar machen. Dazu wird eine sehr dünne Schicht eines optischen Mediums (die eine kleinere Brechungszahl als das Glas haben muss) auf die Brille oder das Display aufgedampft. Das Licht wird sowohl an der Oberseite wie an der Unterseite reflektiert.

Da zwischen dem an der Ober- und Unterseite reflektierten Anteile so ein Gangunterschied entsteht, der dem Doppelten der Schichtdicke entspricht, kann es je nach Lichtfarbe und Schichtdicke zur Auslöschung kommen.

Da der Gangunterschied allerdings nicht nur von der Schichtdicke abhängt, sondern auch von der Lichtfarbe und vom Betrachtungswinkel, können nicht alle Lichtfarben bei jedem Winkel gleichermaßen ausgelöscht werden. Es lassen sich jedoch mehrere Schichten übereinander aufbringen, so dass man schließlich eine Minderung der Reflexe um ca. 90% erreicht.

Ausführliche Informationen zur Vergütung von Gläsern findest Du hier.

weiter mit Polarisation von Licht

zurück