Das Massenspektrometer nach Bainbridge

Mit Hilfe von Magnetfeldern lassen sich geladene Teilchen ablenken, wobei die Ablenkung von der Masse der Teilchen abhängt. Dieses Phänomen lässt sich dafür nutzen, die Masse von (geladenen) Teilchen zu bestimmen.

Im Abschnitt “Bewegte Ladungsträger im Magnetfeld” haben wir durch die Ablenkung von Elektronen im Magnetfeld eine Formel für die Masse der Elektronen hergeleitet:

Es gilt:     m_{e}=\dfrac {Ber}{v_{s}}        bzw. allgemein für eine Ladung q        m=\dfrac {Bqr}{v_{s}}

Für den Radius der Kreisbahn, auf die die geladenen Teilchen durch ein homogenes Magnetfeld der Stärke <em>B gezwungen werden, gilt also:

r=\dfrac {m\cdot v}{B\cdot q}

Der Radius hängt also neben der Masse der geladenen Teilchen auch von ihrer Geschwindigkeit ab.

Damit man aus der Ablenkung geladener Teilchen auf die Masse schließen kann, müssen alle zu untersuchenden Teilchen die gleiche Ladung q und die gleiche Geschwindigkeit besitzen.

Geschwindigkeitsfilter nach Wien

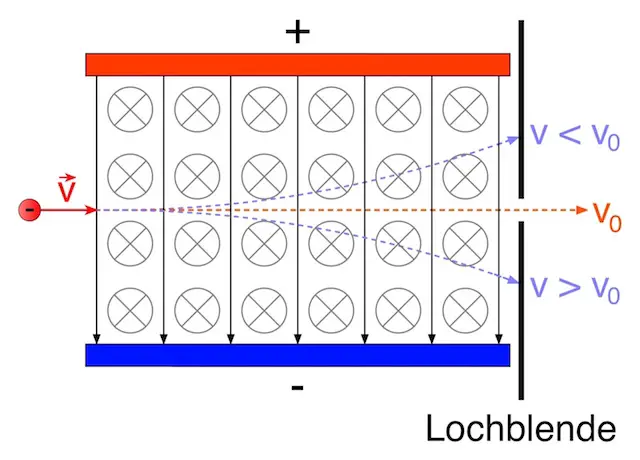
Um nur Teilchen mit einer definierten Geschwindigkeit zu erhalten, kann man einen Geschwindigkeitsfilter nach Wien benutzen. Ein solcher Filter besteht aus einem gekreuzten elektrischen und magnetischen Feld:

Geschwindigkeitsfilter nach Wien

Die geladenen Teilchen gelangen in einen Plattenkondensator, indem zusätzlich zum elektrischen Feld ein magnetisches Feld existiert. Die magnetischen Feldlinien stehen senkrecht auf den elektrischen Feldlinien.

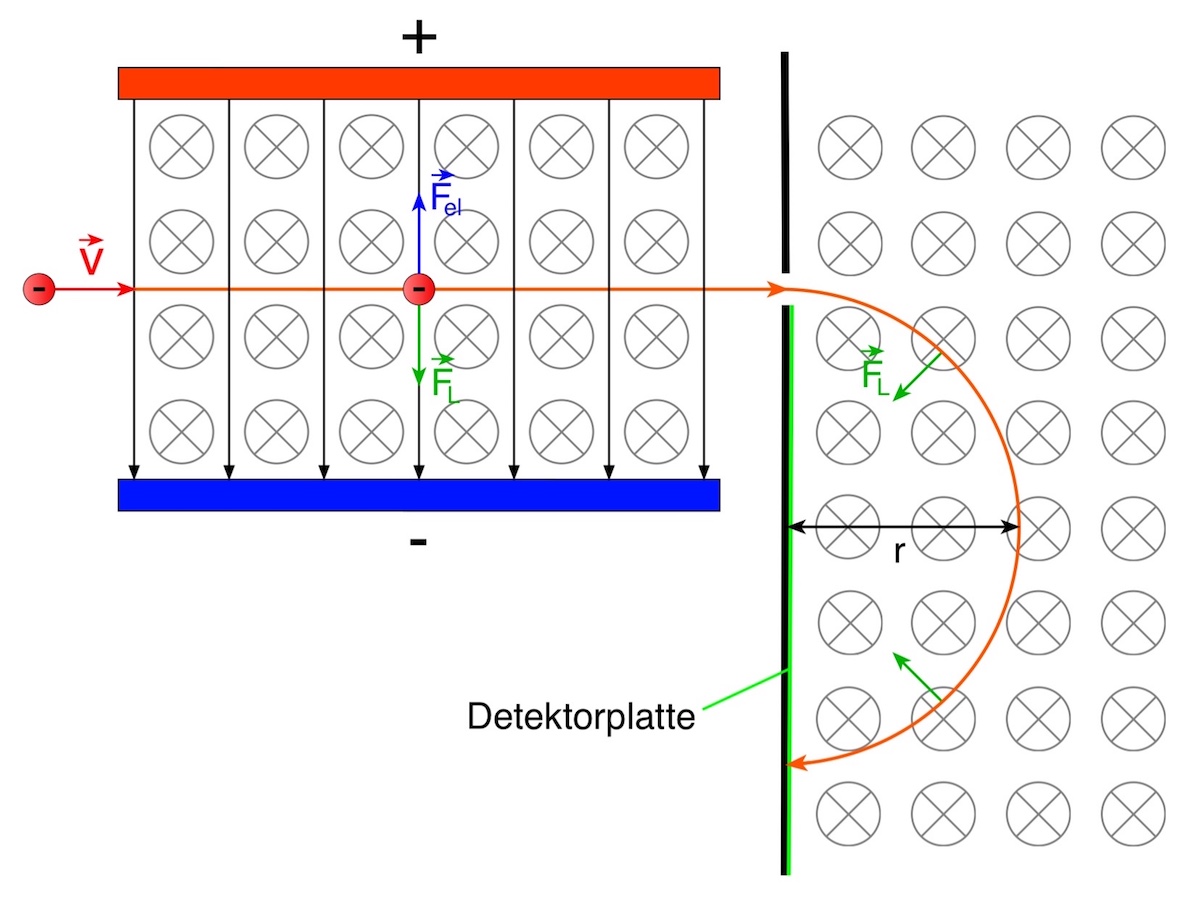
Ein negativ geladenes Teilchen, das sich senkrecht zu deb elektrischen und magnetischen Feldlinien bewegt, erfährt durch das elektrische Feld die Kraft F_{el}=qE nach oben und durch das magnetische Feld die Lorentzkraft F_{L}=qvB nach unten.

Für den Fall, dass beide Kräfte gleich groß sind, werden die Teilchen nicht abgelenkt und können so den Plattenkondensator auf geradem Weg durchqueren.

In diesem Fall gilt:

F_{el}=F_{L}

q\cdot E=q\cdot v\cdot B

Die Ladung q lässt sich kürzen, sie spielt also keine Rolle.

Die Geschwindigkeit, für die die Bedingung erfüllt ist, beträgt demnach

v=\dfrac {E}{B}

Alle Teilchen mit dieser Geschwindigkeit passieren den Filter ohne Richtungsänderung.

Bei Teilchen mit kleinerer Geschwindigkeit überwiegt die elektrische Kraft, daher werden diese nach oben abgelenkt.

Bei Teilchen mit größerer Geschwindigkeit überwiegt die Lorentzkraft, daher werden diese nach unten abgelenkt.

Alle Teilchen, die durch die Lochblende gelangen, haben demnach die gleiche Geschwindigkeit – unabhängig von ihrer Masse und Ladung. Daher wirkt die Anordnung als Geschwindigkeitsfilter.

Hinweis:

Da ungeladene Teilchen weder im elektrischen noch im magnetischen Feld eine Kraft erfahren, würden auch alle ungeladenen Teilchen unabhängig von ihrer Geschwindigkeit den Filter passieren.

Massenspektrometer nach Bainbridge

Um die Masse der Teilchen zu untersuchen, lässt man den Teilchenstrahl hinter dem Wienfilter in ein weiteres Magnetfeld B’ eintreten. Auf die geladenen Teilchen wirkt nun nur die Lorentzkraft, die diese wie im Fadenstrahlrohr auf eine Kreisbahn zwingt.

Da alle Teilchen die gleiche Geschwindigkeit haben, hängt der Bahnradius für Teilchen gleicher Ladung im Magnetfeld nur von der Masse der Teilchen ab bzw. für Teilchen unterschiedlicher Ladung von ihrer spezifischen Ladung \dfrac {q}{m}.

Massenspektrometer nach Bainbridge

Die Lorentzkraft auf geladene Teilchen im zweiten Magnetfeld B’ beträgt

F_{L}=q\cdot v\cdot B'

Sie wirkt als Zentripetalkraft und zwingt die Teilchen auf eine Kreisbahn mit dem Radius r. Wir können also wieder den Ansatz des Kräftegleichgewichts verwenden:

F_{L}=F_{Z}

q\cdot v\cdot B'=m\dfrac {v^{2}}{r}

Damit ergibt sich für den Radius

r=\dfrac {m\cdot v}{q\cdot B'}

Für die Geschwindigkeit der Teilchen gilt (s.o.):

v=\dfrac {E}{B}

Eingesetzt ergibt sich:

r=\dfrac {m\cdot E}{q\cdot B\cdot B'}

Sind die Magnetfelder B und B’ gleich groß, gilt:

r=\dfrac {m\cdot E}{q\cdot B^{2}}

Teilchen unterschiedlicher Masse treffen also in einem anderen Abstand d=2r auf den Detektor.

Aus dem Abstand lässt sich dann die Masse der Teilchen berechnen, indem man die Gleichung nach m umstellt:

m=\dfrac {q\cdot B\cdot B'\cdot r}{E}        bzw.        m=\dfrac {q\cdot B^{2}\cdot r}{E}        für  B = B'

Hinweis:

Es lassen sich auf diese Art nur die Massen geladener Teilchen bestimmen. Außerdem muss die Ladung bekannt sein, denn Teilchen mit doppelter Ladung und doppelter Masse treffen an der gleichen Stelle auf die Detektorplatte.

zurück