Wellenphänomene

Phänomene von Wellen

Nachfolgend werden einige typische Wellenphänomene beschrieben, die mit Hilfe der Wellenwanne beobachtet werden können. Diese Phänomene lassen sich bei allen Arten von Wellen nachweisen.

Reflexion

Trifft eine Welle auf eine ebene Oberfläche, dann wird sie reflektiert.

Es gilt das Reflexionsgesetz (Einfallswinkel = Reflexionswinkel: α = β).

Brechung

Trifft eine Welle unter einem Winkel α ≠ 0 auf einen Bereich, in dem sich die Ausbreitungsgeschwindigkeit ändert (bei Wasserwellen durch Veränderung der Wassertiefe), so ändert sich ihre Ausbreitungsrichtung.

Es gilt das Brechungsgesetz:       

Dabei ist n die Brechungszahl und c die Ausbreitungsgeschwindigkeit der Wellen in den Bereichen 1 und 2.

(Dieses Gesetz gilt ebenso für die Brechung von Licht.)

Beugung

Trifft eine Welle auf eine Kante oder einen Spalt, so ändert sich ihre Richtung, und die Welle dringt auch in den sog. Schattenraum ein. An einem Spalt bilden sich kreisförmige Wellen, die sich in alle Richtungen ausbreiten (s. Abbildung unten). Diese Erscheinung nennt man Beugung.

Die Beugung lässt sich mit dem Huygens’schen Prinzip erklären.

Dieses Prinzip ist benannt nach dem niederländische Physiker Christian Huygens (1629-1695), der sich ab 1681 vor allem mit dem Wesen des Lichts beschäftigte. Er gilt als einer der Begründer der Wellenoptik.

Das Huygens’sche Prinzip

Jeder Punkt einer Wellenfront kann als Ausgangspunkt für kreis- oder kugelförmige Elementarwellen angesehen werden.

Diese Elementarwellen besitzen die gleiche Ausbreitungsgeschwindigkeit wie die ursprüngliche Welle.

Die Einhüllende aller Elementarwellen bildet die neue Wellenfront:

Skizze folgt

Hinweis:

Das Huygens’sche Prinzip wurde vom französischen Physiker Augustin Jean Fresnel (1788-1827) erweitert. Bei Huygens selbst fehlten noch Begriffe wie Wellenlänge und Frequenz, so dass die Beugung erst mit dieser Erweiterung erklärt werden kann.

Eine ausführliche Beschreibung zum Huygens’schen Prinzip mit mehreren Animationen findet man bei Leifiphysik.

 

Überlagerung von Wellen

Weitere Phänomene lassen sich beobachten, wenn sich mehrere Wellen überlagern.

Beispiel: Wirft man gleichzeitig zwei Steine ins Wasser, erkennt man, dass sich die entstehenden kreisförmigen Wellen durchdringen, ohne einander zu stören. Dies gilt für alle Arten von Wellen.

Wellen durchdringen einander, ohne sich in ihrer Ausbreitung zu stören.

Interferenz

Die Überlagerung von Wellen gleicher Frequenz bezeichnet man als Interferenz.

Bei einer solchen Überlagerung bilden sich Bereiche der Verstärkung und der Abschwächung bzw. Auslöschung – je nachdem, welche Phasen zweier Wellen aufeinandertreffen.

Die Auslenkung der resultierenden Welle ergibt sich aus der Addition der Auslenkungen der einzelnen Wellen:

Verstärkung

Treffen zwei Wellenberge bzw. zwei Wellentäler aufeinander (zwei gleiche oder ähnliche Phasen), so bildet sich ein noch höherer Wellenberg bzw. ein noch tieferes Wellental – die Auslenkung wird also verstärkt.

Abschwächung bzw. Auslöschung

Trifft der Wellenberg einer Welle auf ein Wellental der anderen Welle (die Phasenverschiebung zwischen den Wellen beträgt dann ein ungeradzahliges Vielfaches der halben Wellenlänge), kommt es zur Abschwächung – die positive und negative Auslenkung addieren sich. Sind die Amplituden beider Wellen gleich groß, so kommt es zur völligen Auslöschung.

Die Auslenkungen interferierender Wellen addieren sich

Bei der Überlagerung von Wellen addieren sich an jeder Stelle die Auslenkungen der einzelnen Wellen. Es entsteht eine resultierende Welle mit der gleichen Frequenz. Ihre Amplitude hängt vom Phasenunterschied der beiden Wellen ab.

Nach der Durchdringung laufen die beiden Wellen ungestört weiter.

Die folgenden Bilder zeigen zwei Wellen gleicher Amplitude und gleicher Frequenz (rot und grün) mit verschiedenen Phasenlagen. Die resultierende Welle (violett) ergibt sich aus der Summe der Auslenkungen der beiden sich überlagenden Wellen.

Je nach Phasenbeziehung ist die Amplitude der resultierenden Welle größer oder kleiner als die der einzelnen Wellen:

Verstärkung

Abschwächung

maximale Verstärkung

komplette Auslöschung

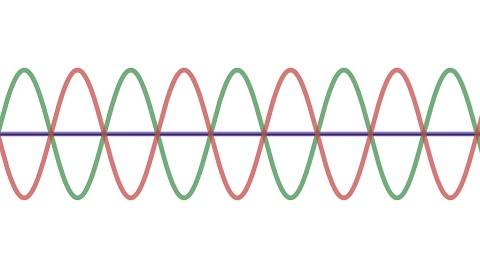
Der Gangunterschied

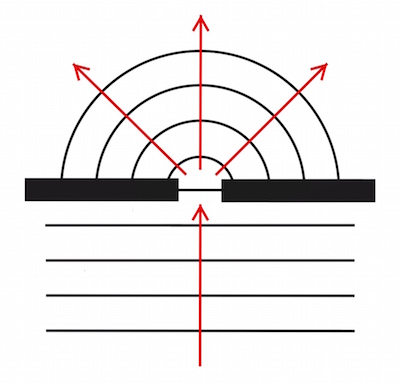
Als Gangunterschied δ oder Δs bezeichnet man die Wegdifferenz (den Wegunterschied) zweier oder mehrerer zusammenhängender Wellen, die sich überlagern.

Der Gangunterschied bestimmt die Phasenbeziehung zwischen den interferierenden Wellen und damit, ob sich diese verstärken oder abschwächen.

Für bestimmte Bedingungen kommt es zu einer maximalen Verstärkung oder zur völligen Auslöschung der Wellen:

Maximale Verstärkung (konstruktive Interferenz)

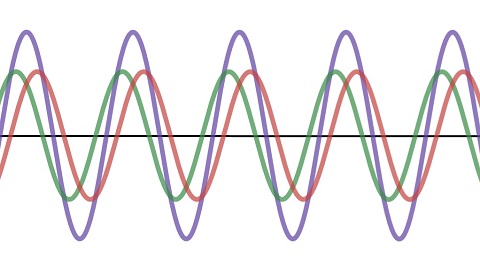
Zwei interferierende Wellen werden maximal verstärkt, wenn genau ein Wellenberg auf einen Wellenberg bzw. ein Wellental auf ein Wellental trifft (s.o.). Die Wellen sind dann phasengleich.

Zur maximalen Verstärkung kommt es, wenn der Gangunterschied δ zwischen den interferierenden Wellen Null oder ein ganzzahliges Vielfaches der Wellenlänge λ beträgt.

Bedingung für maximale Verstärkung:

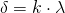      mit k = 0, 1, 2, 3,…

Auslöschung (destruktive Interferenz)

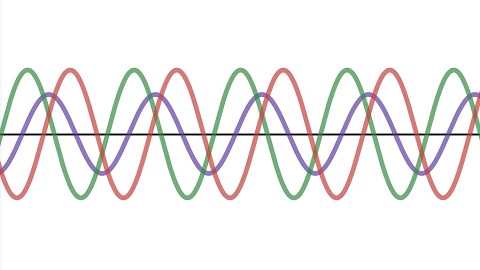
Zwei interferierende Wellen werden ausgelöscht, wenn ein Wellenberg genau auf ein Wellental trifft. Die Wellen sind dann um eine halbe Wellenlänge phasenverschoben.

Zur Auslöschung kommt es, wenn der Gangunterschied zwischen den interferierenden Wellen ein ungeradzahliges Vielfaches der halben Wellenlänge beträgt.

Bedingung für Auslöschung:

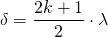      (Der Zähler ist auf diese Weise immer ungerade)

bzw.

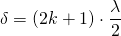    mit k = 0, 1, 2, 3,…

Weitere Wellenphänomene

Wellen können absorbiert, gestreut oder polarisiert werden. Darüber hinaus kann auch Dispersion auftreten. Diese und weitere Wellenphänome werden im folgenden kurz erklärt:

Absorption

Beim Durchgang von Wellen durch Stoffe erfolgt eine Abschwächung oder Absorption, die sich durch den Absorptionsgrad erfassen lässt. Damit verringert sich die Energie der Welle. Die Energie wird vom Stoff aufgenommen.

Streuung

Hindernisse, die im Vergleich zur Wellenlänge sehr klein sind, werden zu Zentren von Elementarwellen, die sich von dort nach allen Richtungen ausbreiten. Dieser Vorgang wird als Streuung bezeichnet. Er spielt vor allem in der Optik eine wichtige Rolle.

Polarisation

Wird bei Transversalwellen unterschiedlicher Schwingungsrichtung eine bestimmte Schwingungsrichtung herausgefiltert, so spricht man von Polarisation. Die Wellen schwingen dann in einer Schwingungsrichtung. Sie sind linear polarisiert.

Dispersion

Bei der Ausbreitung in einem Stoff hängt die Ausbreitungsgeschwindigkeit einer Welle in der Regel von der Wellenlänge bzw. von der Frequenz ab. Diese Erscheinung wird als Dispersion bezeichnet. Sie spielt vor allem in der Optik eine Rolle.

Bei Schallwellen in Luft tritt keine Dispersion auf. Es gibt deshalb bei der Übertragung von Sprache oder Musik durch die Luft auch keine Verzerrungen durch Dispersion.

Schwebung

Ein typisches Phänomen von Schallwellen ist die Schwebung. Diese tritt aber auch im Bereich der Signalverarbeitung und bei elektromagnetischen Wellen auf. Unter einer Schwebung versteht man das Resultat zweier sich überlagernder Schwingungen, die sich in ihrer Frequenz nur wenig voneinander unterscheiden.

Es entsteht eine resultierende Schwingung, deren Frequenz dem Mittelwert der beiden einzelnen Frequenzen entspricht.

Es gilt:     .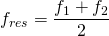

Die Amplitude variiert mit der Frequenz   .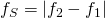

Diese Frequenz wird als Schwebungsfrequenz bezeichnet.

In der folgenden Abbildung sind zwei Schwingungen gleicher Amplitude dargestellt (grün und rot), deren Frequenz sich ein wenig unterscheidet.

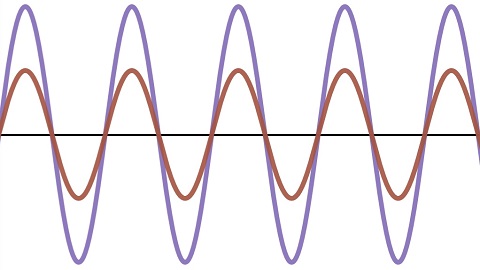
Darunter sieht man die resultierende Schwingung, deren Amplitude sich mit der Schwebungsfrequenz ändert. Die Amplitude ist am größten, wenn die Einzelschwingungen phasengleich sind und am kleinsten, wenn die Phasenverschiebung genau einer halben Periode entspicht:

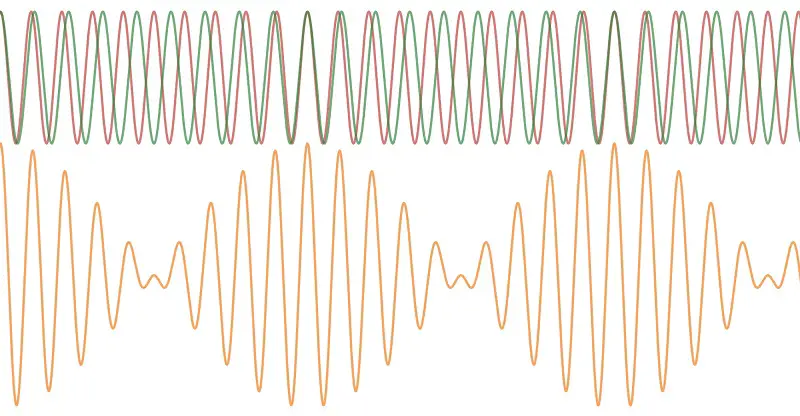
Die resultierende Schwingung (unten) ergibt sich aus der Addition der Auslenkungen der einzelnen Schwingungen zu jedem Zeitpunkt.