Eine Maschine, die die gesamte zugeführte Wärme in mechanische Energie umwandelt, bezeichnet man als Perpetuum mobile zweiter Art.
Eine andere Formulierung des zweiten Hauptsatzes ist demnach:
Ein Perpetuum mobile zweiter Art gibt es nicht.
Aus dem zweiten Hauptsatz folgt die Erkenntnis, dass die Richtungen der Energieumwandlungen nicht gleichwertig sind. So ist es zwar möglich, mechanische Energie vollständig in Wärme umzuwandeln, anders herum erfolgt die Umwandlung jedoch nicht vollständig.
Der ideale Wirkungsgrad
Wenn der Wirkungsgrad stets kleiner als 1 ist, stellt sich die Frage: Wie groß kann der Wirkungsgrad maximal werden, und wovon hängt er ab?
Aus dem p-V-Diagramm des Stirling’schen Kreisprozesses auf der vorherigen Seite geht hervor, dass die umschlossene Fläche und damit die verrichtete Arbeit umso größer ist, je größer der Abstand der beiden Isothermen ist, also je größer die Differenz der beiden Temperaturen T1 und T2 ist.
Für den maximalen Wirkungsgrad, der bei einem Kreisprozess erreicht werden kann, gilt:
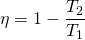 oder
oder 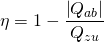
Hinweis: Die Temperatur T1 ist höher als T2, also gilt: 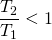
Beispielrechnung zum idealen Wirkungsgrad
In einem Dieselmotor betrage 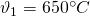 und
und 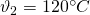 .
.
Die Berechnung des Wirkungsgrades mit der o.g. Formel beträgt
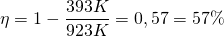
Der tatsächliche Wirkungsgrad eines Dieselmotors beträgt jedoch nur etwa 0,4 bzw. 40%.
Der Wirkungsgrad realer Wärmekraftmaschinen liegt aufgrund von Reibung und Wärmeverlusten meist erheblich unterhalb des idealen Wirkungsgrades.
Carnot-Prozess
Der französische Wissenschaftler Sadi Carnot (1796-1832) fand und beschrieb im Jahre 1824 einen idealen Kreisprozess, der unter allen möglichen Kreisprozessen den maximalen Wirkungsgrad besitzt.
Bei diesem sog. Carnot’schen Kreisprozess handelt es sich um einen theoretischen idealisierten Kreisprozess, der sich nicht realisieren lässt. Er setzt als Arbeitsmedium eine ideales Gas voraus und geht von reversiblen (umkehrbaren) Zustandsänderungen aus.
Der Wirkungsgrad des Carnot’schen Kreisprozesses entspricht dem oben beschriebenen idealen Wirkungsgrad.
Der Carnot’sche Kreisprozess setzt sich aus folgenden vier Zustandsänderungen zusammen:
1. Isotherme Expansion
2. Adiabatische Expansion
3. Isotherme Kompression
4. Adiabatische Kompression
Bei einer adiabatischen Zustandsänderung wird keine Wärme mit der Umgebung ausgetauscht. Es ändern sich alle drei Zustandsgrößen.
Ein Beispiel für eine adiabatische Kompression ist das schnelle Zusammendrücken einer Luftpumpe, so dass die zugeführte mechanische Arbeit vollständig in innere Energie des Gases umgewandelt wird und zu einer Temperaturerhöhung führt.
Erfolgt die Kompression langsamer, so gibt die Luft einen Teil der Wärme an die Umgebung ab.
Folgendes Bild zeigt das p-V-Diagramm eines Carnot’schen Kreisprozesses:
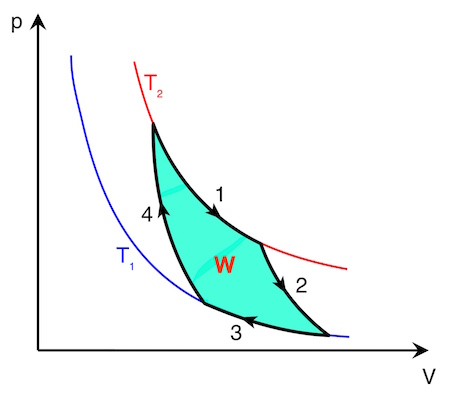
Der deutsche Physiker Rudolf Clausius verknüpfte die Idee von Carnot mit dem ersten Hauptsatz und zeigte, dass bei jedem Kreisprozess Wärme von einem wärmeren Reservoir in ein kälteres Reservoir fließt.
Es gilt: Wärme kann niemals von selbst aus einen Körper niedrigerer Temperatur auf einen Körper höherer Temperatur übergehen. Aus dieser Erkenntnis folgt direkt der zweite Hauptsatz.
![]() (Eta):
(Eta):![]()
