Das Bohrsche Atommodell

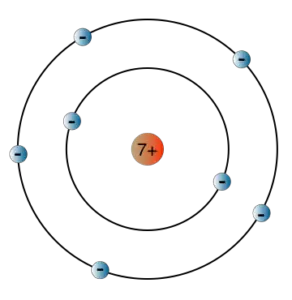
Bohrsches Atommodell

Wir wollen nun mit dem Bohrschen Atommodell, welches wir bereits im Abschnitt zur quantenhaften Emission und Absorption kennengelernt haben, einige Berechnungen durchführen.

Auch wenn das Bohrsche Atommodell deutliche Schwächen hat und inzwischen vom quantenmechanischen Atommodell abgelöst wurde, so lassen sich mit ihm – zumindest für das Wasserstoffatom – viele Berechnungen durchführen, die zu richtigen Ergebnissen führen.

Mit Bohrs Postulaten lassen sich die empirischen Formeln von Johann Balmer und Johannes Rydberg logisch herleiten, die über 20 Jahre lang unverstanden blieben. Die empirische Größe der Rydberg-Konstante konnte Bohr auf Naturkonstanten zurückführen.

Trotz aller Schwächen hat sich das Bohrsche Atommodell mit um den Atomkern kreisenden Elektronen in den Köpfen vieler Menschen festgesetzt.

Die Berechnungen, die sich damit durchführen lassen, tragen außerdem noch heute zum Verständnis des quantenmechanischen Atommodells bei.

Die Bohrschen Postulate

Niels Bohr

Auf der Bahn des Elektrons um den Atomkern sind nur ganz bestimmte Bahnen erlaubt, wobei jede Bahn einer Energiestufe entspricht. Niels Bohr konnte allerdings selbst nicht erklären, warum die Elektronen auf ihrer Bahn um den Kern keine Energie abgeben und dadurch in den Kern stürzen, wie es nach den Gesetzen der Elektrodynamik der Fall sein müsste.

Er umging die Probleme seines Atommodells mit verschiedenen Annahmen, die als Bohr’sche Postulate bezeichnet werden. Diese wollen wir hier noch einmal nennen:

1. Im Atom existieren stabile Bahnen, auf denen die Elektronen kreisen, ohne Energie abzugeben.

Für den energetischen Aspekt eines Elektronenübergangs von einer Bahn zu einer anderen soll gelten:

2. Jede erlaubte Elektronenbahn entspricht einer bestimmten Energie E der Elektronen. Wechselt ein Elektron die Bahn, so ist die Energie des emittierten bzw. absorbierten Photons gleich der Energiedifferenz dieser Bahnen.

Dabei gilt: ΔE = h · f

3. Bohr’sche Quantenbedingung

Für den Zusammenhang zwischen dem Bahnumfang U_n, der Elektronenmasse m_e, der Elektronengeschwindigkeit v_n sowie der planckschen Konstante h gilt:

Die Bohr’sche Quantenbedingung lautet: U_n · m_e · v_n = n · h

wobei die Zahlen n = 1, 2, 3, … den Energiestufen entspricht. Sie entsprechen den Hauptquantenzahlen.

Berechnung der diskreten Energiezustände im Wasserstoffatom

Wir wollen mit Hilfe der Bohrschen Annahmen die Energiestufen und damit die möglichen Energiedifferenzen, aus denen sich die möglichen Spektrallinien ergeben, berechnen:

Nach dem 2. Bohrschen Postulat gilt für die Energie eines emittierten oder absorbierten Photons

$hf=E_{m}-E_{n}=\Delta E$ ,

wobei $E_{n}$ die Energie des Elektrons auf der n-ten Bahn ist.

Die Gesamtenergie eines Elektrons setzt sich zusammen aus potentieller und kinetischer Energie (potentielle Energie aufgrund der Coulomb-Kraft und des Abstandes vom Kern).

Für die Energie eines Elektrons auf der n-ten Bahn gilt also

$E=E_{kin,n}+E_{pot,n}$

Wir wollen nun jeweils die kinetische und die potentielle Energie berechnen.

Für die kinetische Energie eines Elektrons gilt

$E_{kin,n}=\frac {1}{2}m_{e} \left( v_{n}\right) ^{2}$

(Dabei ist die Geschwindigkeit auf der n-ten Bahn $v_{n}$ zunächst unbekannt.)

Die potentielle Energie im Radialfeld lässt sich mit Hilfe des Coulomb-Gesetzes berechnen:

$E_{pot,n}=\dfrac {1}{4\pi\varepsilon_{0}}\cdot \dfrac {Q_{1}\cdot Q_{2}}{r_{n}}$

Die Ladungen Q₁ und Q₂ sind die Ladungen von Kern und Elektron, also e und -e.

Damit ergibt sich für die potentielle Energie

$E_{pot,n}=-\dfrac {e^{2}}{4\pi\varepsilon_{0}r_{n}}$

(Der Radius der n-ten Bahn $r_{n}$ ist noch unbekannt.)

Berechnung von Radius und Geschwindigkeit

In den Gleichungen für potentielle und kinetische Energie sind sowohl Radius als auch Geschwindigkeit noch unbekannt. Diese sollen nun ermittelt werden.

Für die Kreisbahn des Elektrons gilt: Die elektrische (Coulomb-) Kraft wirkt als Zentripetalkraft, die das Elektron auf eine Kreisbahn mit dem Radius r zwingt.

Damit lassen sich elektrische Kraft $F_{el}$ und Zentripetalkraft $F_{z}$ gleichsetzen:

$F_{z}=F_{el}$ (Zur Erinnerung: Für die Zentripetalkraft gilt: $F_{z}=\dfrac {mv^{2}}{r}$ )

Setzen wir die Formeln für die beiden Kräfte ein, erhalten wir

$\dfrac {m_{e}\left(v_{n}\right)^{2}}{r_{n}}=\dfrac {e^{2}}{4\pi\varepsilon_{0}\left(r_{n}\right)^{2}}$

Wir multiplizieren diese Gleichung mit $\left( r_{n}\right)^{2}$ und erhalten

$r_{n}m_{e}\left(v_{n}\right)^{2}=\dfrac {e^{2}}{4\pi\varepsilon_{0}}$ (1)

Außerdem gilt die Bohrsche Quantenbedingung (s.o.):

$U_{n}\cdot m_{e}\cdot v_{n}=nh$ mit $U_{n}=2\pi r_{n}$

Wenn man darin für den Umfang $U_{n}=2\pi r_{n}$ einsetzt und anschließend durch $2\pi$ teilt, ergibt sich:

$r_{n}m_{e}v_{n}=\dfrac {nh}{2\pi}$

Nun multiplizieren wir diese Gleichung mit $v_{n}$ und erhalten

$r_{n}m_{e}\left(v_{n}\right)^{2}=\dfrac {nhv_{n}}{2\pi}$

Auf der linken Seite steht nun das gleiche wie in (1), also sind auch die rechten Seiten beider Gleichungen gleich.

Damit gilt:

$\dfrac {nhv_{n}}{2\pi}=\dfrac {e^{2}}{4\pi\varepsilon_{0}}$

Nun müssen wir diese Gleichung nur noch nach $v_{n}$ umstellen.

Damit ergibt sich für die Geschwindigkeit $v_{n}$ :

$v_{n}=\dfrac {e^{2}}{2\varepsilon_{0}nh}$

Die Geschwindigkeit eines Elektrons auf der n-ten Bahn lässt sich also allein aus Naturkonstanten berechnen.

Nun wollen wir noch den Radius berechnen. Dazu setzen wir den gerade ermittelten Ausdruck für die Geschwindigkeit $v_{n}$ in (1) ein und erhalten:

$r_{n}m_{e}\cdot \left( \dfrac {e^{2}}{2\varepsilon_{0}nh}\right) ^{2}=\dfrac {e^{2}}{4\pi\varepsilon_{0}}$

Diese Gleichung müssen wir nur noch nach $r_{n}$ auflösen.

Wir erhalten für den Radius $r_{n}$ :

$r_{n}=\dfrac {h^{2}\varepsilon_{0}}{\pi m_{e}e^{2}}\cdot n^{2}$

Es ergeben sich feste Bahnen, die sich allein aus Naturkonstanten berechnen lassen und nur von der Hauptquantenzahl n abhängen!

Berechnet man auf diese Weise den Radius der Kreisbahn eines Elektrons, ergibt sich für den Grundzustand (n = 1) ein Radius von

r₁ = 5,29 · 10^-11m Dieser Radius ist der sog. Bohrsche Radius.

Das bedeutet, der Atomdurchmesser beträgt etwa 10^-10m. Das stimmt mit auf anderen Wegen gefundenen Werten überein.

Berechnung der diskreten Energiewerte

Nun, da wir Radius und Geschwindigkeit in Abhängigkeit vom Energiezustand ermittelt haben, können wir die Energien berechnen.

Geschwindigkeit $v_{n}=\dfrac {e^{2}}{2\varepsilon_{0}nh}$ Radius $r_{n}=\dfrac {h^{2}\varepsilon_{0}}{\pi m_{e}e^{2}}\cdot n^{2}$

Damit ergibt sich für die kinetische Energie

$E_{kin,n}=\frac {1}{2}m_{e}\left(v_{n}\right)^{2}=\frac {1}{2}m_{e}\dfrac {e^{4}}{4\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}$

Wir schreiben das nun etwas kompakter und erhalten:

Die kinetische Energie eines Elektrons auf der n-ten Bahn beträgt

$E_{kin,n}=\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}$

Für die potentielle Energie ergibt sich:

$E_{pot,n}=-\dfrac {e^{2}}{4\pi\varepsilon_{0}r_{n}}=-\dfrac {m_{e}e^{4}}{4\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}$

Die potentielle Energie eines Elektrons auf der n-ten Bahn beträgt

$E_{pot,n}=-\dfrac {m_{e}e^{4}}{4\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}$

Nun lässt sich aus der Summe der beiden Energien die Gesamtenergie berechnen. Man beachte dabei, dass die potentielle Energie negativ ist.

$E_{ges,n}=E_{kin,n}+E_{pot,n}$

Wir setzen die oben hergeleiteten Gleichungen ein und erhalten

$E_{ges,n}=\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}-\dfrac {m_{e}e^{4}}{4\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}$

Die potentielle Energie ist vom Betrag her genau doppelt so groß wie die kinetische Energie, hat jedoch ein negatives Vorzeichen. Die Gesamtenergie ist also negativ und vom Betrag her gleich der kinetischen Energie.

Die Gesamtenergie eines Elektrons auf der n-ten Bahn beträgt

$E_{ges,n}=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}$

Mit dieser Gleichung lassen sich nun die Energien $E_{n}$ für alle Energiezustände (n = 1, 2, 3, …) berechnen und deren Wert als Linien entlang einer Energieachse darstellen. So erhält man das schon bekannte Energieniveauschema des Wasserstoffatoms!

Diskrete Energieniveaus im Wasserstoffatom

Das Wasserstoffatom besitzt diskrete Energiezustände $E_{n}$ , die sich aus den unterschiedlichen Bahnen des Elektrons ergeben:

Die Energieniveaus im Wasserstoffatom betragen

$E_{ges,n}=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}$ bzw. $E_{ges,n}=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}}\cdot \dfrac {1}{n^{2}}$

Berechnet man mit dieser Formel die Energie für den Grundzustand (n = 1), erhält man

$E_{1}=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}}=-2,18\cdot 10^{-18}\, J=-13,6\, eV$

Das ist genau der Wert, den wir bereits mit der Rydberg-Formel erhalten haben.

Die Energien für die anderen Zustände unterscheiden sich nur um den Faktor $\dfrac {1}{n^{2}}$ , daher kann man vereinfacht schreiben:

Die Energiezustände $E_{n}$ im Wasserstoffatom lassen sich berechnen mit

$E_{n}=E_{1}\cdot \dfrac {1}{n^{2}}$ und damit $E_{n}=-13,6\, eV\cdot \dfrac {1}{n^{2}}$

Bahnradius, Geschwindigkeit und Energie eines Elektrons im Wasserstoffatoms lassen sich also allesamt aus Naturkonstanten berechnen und hängen nur von der Hauptquantenzahl n ab.

Die Quantenzahl n bestimmt den Energiezustand des Atoms.

Berechnung der Energiedifferenzen und Spektrallinien

Wechselt eine Elektron die Bahn und damit den Energiezustand, so wird ein Photon mit der Frequenz $f=\dfrac {\Delta E}{h}$ absorbiert oder emittiert.

Wir wollen nun noch die möglichen Energiedifferenzen $\Delta E$ zwischen zwei Energiezuständen $E_{m}$ und $E_{n}$ berechnen.

$\Delta E=E_{m}-E_{n}$

Setzen wir die Energien für die Zustände m und n ein, ergibt sich

$\Delta E=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}m^{2}}-\left( -\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}\right)$

bzw.

$\Delta E=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}m^{2}}+\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}$

Dabei kann man den Term $-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}}$ ausklammern und erhält

$\Delta E=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}}\cdot \left(\dfrac {1}{m^{2}}-\dfrac {1}{n^{2}}\right)$

Hinweis:

Der Term $-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}}$ entspricht dabei der Grundzustandsenergie $E_{1}=-13,6\, eV$ .

Diese wird auch als Rydberg-Energie bezeichnet.

Vertauscht man die beiden Subtrahenden innerhalb der Klammer, fällt das Minuszeichen weg und man erhält

$\Delta E=\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}}\cdot \left(\dfrac {1}{n^{2}}-\dfrac {1}{m^{2}}\right)$

Nun schreiben wir anstelle von $\Delta E$ den Ausdruck $hf$ :

$hf=\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}}\cdot \left(\dfrac {1}{n^{2}}-\dfrac {1}{m^{2}}\right)$ | $:h$

Wir teilen die Gleichung durch h und erhalten für die Frequenz

$f=\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{3}}\cdot \left(\dfrac {1}{n^{2}}-\dfrac {1}{m^{2}}\right)$ ,

wobei $\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{3}}=\dfrac {13,6\, eV}{h}$ die Rydberg-Frequenz R ist!

Damit erhält man genau die schon im vorherigen Abschnitt genannte Formel von Johannes Rydberg, die dieser bereits 1890 aufstellte:

Rydberg-Formel $f=R\cdot \left(\dfrac {1}{m^{2}}-\dfrac {1}{n^{2}}\right)$ (mit n > m, ansonsten anders herum)

Schwächen des Bohrschen Atommodells

Trotz dieser erstaunlichen Zusammenhänge, die das Bohrsche Atommodell erklären konnte, hatte es klare Schwächen:

Die Postulate sind unverständlich und erscheinen als willkürliche Annahmen.
Es ist nicht auf andere Atome übertragbar (schon beim He-Atom sind keine Berechnungen mehr möglich).

Bei einer Kreisbahn des Elektrons müsste das Wasserstoffatom die Form einer Scheibe haben. Tatsächlich aber ist es rund (kugelförmig).
Es geht im Widerspruch zur Quantenphysik von der Existenz definierten Elektronenbahnen aus.

Außerdem zeigen sehr genaue Messungen eine natürliche Linienbreite der Spektrallinien.

(→ Erklärung mit Hilfe der Heisenberg’schen Unschärferelation: Δf ist abhängig von der Lebensdauer Δt des angeregten Atoms.)

Auch die Intensitätsverteilung zwischen einzelnen Spektrallinien und damit die Wahrscheinlichkeit für die möglichen Übergänge können mit dem Bohrschen Atommodell nicht erklärt werden.

Ein Schritt zur Lösung: Elektronen haben Welleneigenschaften

Ein erster Schritt zur Lösung gelang De Broglie, der als erster das Elektron als Wellenerscheinung angesehen hat. Seine Vorstellung war die einer stehenden Elektronenwelle um den Atomkern herum:

Diese Wellenerscheinung ist dann stabil, wenn sich eine stehende Welle ausbildet (die Ladungsverteilung ist dann zeitlich konstant; es wird keine Energie abgestrahlt).

Stehende Wellen können sich nur dann bilden, wenn die Wellenlänge ganzzahlig oft in die Bohrsche Kreisbahn passt.

Es muss gelten: $n\cdot \lambda=U_{n}$

Mit der De Broglie-Beziehung $\lambda=\dfrac {h}{p}=\dfrac {h}{m_{e}\cdot v_{n}}$ erhält man:

$\dfrac {n\cdot h}{m_{e}\cdot v_{n}}=U_{n}$

Multipliziert man die Gleichung mit $\left(m_{e}\cdot v_{n}\right)$ , ergibt sich

$U_{n}\cdot m_{e}\cdot v_{n}=n\cdot h$

Das entspricht genau der Bohrschen Quantenbedingung!

Aber: Auch diese Überlegung liefert keine Erklärung, warum das Bohrsche Modell schon beim Helium-Atom versagt.

Den Grund dafür kennen wir jedoch bereits – man fand ihn im Jahre 1925:

Bohr hatte das Elektron als klassisches Teilchen behandelt mit wohldefinierter Bahn und Geschwindigkeit. Da es sich bei Elektronen aber um Quantenobjekte mit Welleneigenschaften handelt, sind für diese nur Wahrscheinlichkeitsaussagen möglich.

Das Problem, einerseits die diskreten Energieniveaus der Atome zu berechnen und andererseits auf die Vorstellung von Elektronenbahnen zu verzichten, wird durch das quantenmechanische Atommodell gelöst.

weiter mit Quantenmechanisches Atommodell

zurück