Die Fotozelle
Bei einer Fotozelle handelt es sich um eine ähnliche Anordnung wie im vorangegangenen Versuch:
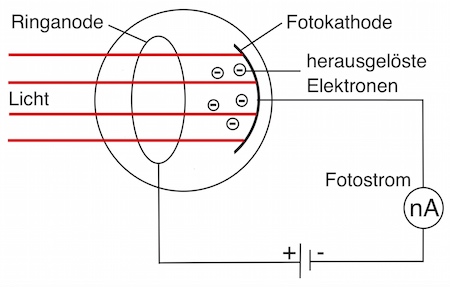
Eine Fotozelle besteht aus einer Metallschicht (meistens wird Cäsium verwendet), der Fotokathode, aus der beim Bestrahlen mit Licht Elektronen herausgelöst werden.
Das Kathodenmaterial besitzt schwach gebundene Elektronen, wodurch diese – im Gegensatz zur Zinkplatte – auch mit sichtbarem Licht herausgelöst werden können.
Zum Auffangen der Fotoelektronen dient ein Metallring, die sogenannte Ringanode.
Beides befindet sich in einer Vakuumröhre, wodurch der Elektronenaustritt erleichtert wird. Dadurch ist es nicht mehr nötig, die Fotokathode negativ zu laden.
Wird die Fotozelle mit Licht bestrahlt, werden Elektronen aus der Fotokathode herausgelöst und gelangen zur Ringanode.
Sind Anode und Kathode nicht miteinander verbunden, entsteht so mit der Zeit auf der Kathode ein Elektronenmangel, während auf der Ringanode ein Elektronenüberschuss entsteht.
Es baut sich dadurch eine Spannung zwischen Anode und Kathode auf: Der Anodenring wird negativ geladen, die Kathode positiv.
Wovon hängt die Spannung zwischen Anode und Kathode ab?
Jedes herausgelöste Elektron bewegt sich auf einen zunehmend negativ geladenen Anodenring zu. Es entsteht also ein immer stärker werdendes elektrisches Feld, welches die Elektronen abbremst. Ist das Feld zu stark, also die Spannung zu groß, können die Fotoelektronen nicht mehr zur Anode gelangen – die Spannung erhöht sich dann nicht mehr weiter.
Die Energie, die die Elektronen benötigen, um das elektrische Feld zwischen Kathode und Anode zu überwinden und so die Anode zu erreichen, entspricht der Energie des elektrischen Feldes:
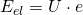
Die kinetische Energie der Elektronen muss also mindestens dieser Energie entsprechen, um die Anode noch zu erreichen.
Je größer die kinetische Energie der schnellsten Fotoelektronen ist, umso größer wird die Spannung.
Steigt die Spannung nicht weiter an, bedeutet das, dass kein Elektron mehr genügend Energie besitzt, um die Anode noch zu erreichen.
Die schnellsten Fotoelektronen haben dann genau die Energie
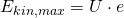 .
.
Hinweis: Nicht alle herausgelösten Elektronen haben die gleiche Energie – diese Energie entspricht der Energie der schnellsten Elektronen.
Mit dem o.g. Zusammenhang kann man ganz einfach aus der Spannung auf die Energie der schnellsten Fotoelektronen schließen.
Wiederholt man den Versuch mit verschiedenen Lichtfarben, so stellt sich heraus:
Die Spannung hängt von der Lichtfarbe ab:
Je größer die Frequenz des verwendeten Lichts, umso größer wird die Spannung.
Dieser Zusammenhang bestätigt die Erkenntnis aus den vorangegangenen Versuchen:
Licht kleinerer Wellenlänge kann offensichtlich mehr Energie auf die Elektronen übertragen als langwelligeres Licht – und zwar unabhängig von der Intensität des Lichts!
Wie viel Energie erhalten die Elektronen durch das Licht, und wovon hängt diese ab?
Um die Energie der schnellsten Fotoelektronen zu bestimmen, müsste man folglich die Spannung, die sich beim Bestrahlen der Fotozelle mit Licht einstellt, messen. Dann ließe sich mit dem o.g. Zusammenhang die Energie der Fotoelektronen berechnen.
Bei der Bestimmung dieser Spannung gibt es jedoch ein Problem:
Auch wenn ein Voltmeter einen hohen Innenwiderstand hat, so fließen doch einige Elektronen durch das Voltmeter hindurch – und damit von der Anode zur Kathode. Doch dadurch sinkt die zu messende Spannung.
Da die Anzahl der Elektronen begrenzt ist (der Fotostrom ist sehr klein; er liegt im Bereich von einigen nA), würden wir also durch den Messprozess selbst die zu messende Größe maßgeblich beeinflussen.
Aus diesem Grund verwendet man eine andere Methode zur Bestimmung der maximalen Energie der Fotoelektronen, die sog. Gegenfeldmethode.


