Die Längenkontraktion

Nicht nur die Zeit ist relativ – auch die Länge eines Körpers bzw. die Entfernung zwischen zwei Punkten ist keine absolute Größe, sondern vom Bezugssystem abhängig. Die sogenannte Längenkontraktion ergibt sich direkt aus der Zeitdilatation.

Um dies zu zeigen, verwenden wir wieder ein Gedankenexperiment:

Eine Rakete (System S’) fliegt mit nahezu Lichtgeschwindigkeit an der Erde (System S) vorbei. In der Rakete befinden sich zwei synchronisierte Lichtuhren A und B, die sich jeweils am Anfang und am Ende der Rakete befinden. Ihr Abstand entspricht damit der Länge l' der Rakete in System S’. Auf der Erde (System S) befindet sich ebenfalls eine Lichtuhr C.

Die Zeit des Vorbeifliegens wird in beiden Systemen S und S’ gemessen.

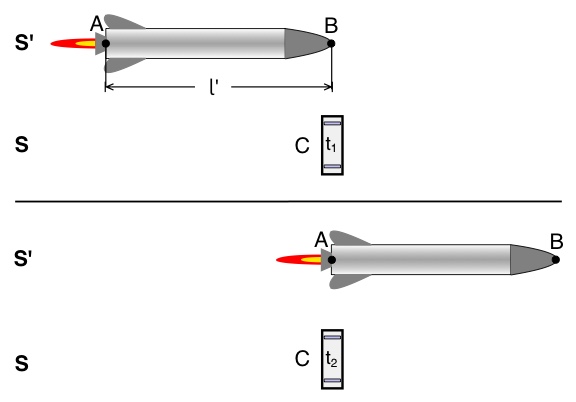
Längenkontraktion Relativitätstheorie

Zu beachten ist hierbei, dass sich in diesem Beispiel in System S’ zwei synchronisierte Lichtuhren befinden. Die Zeitdauer für das Vorbeifliegen in S erscheint in System S’ gedehnt. In S wird also die kürzere Zeit gemessen, so dass gilt:

t<t'   bzw.   t=\dfrac {t'}{\gamma}

Die Zeit des Vorbeifliegens beträgt

in S’:        t'=t\cdot \gamma        Die Zeit t' ist gedehnt gegenüber der Zeit t gemessen in S

Für die Länge der Rakete in System S’ gilt:

l'=v\cdot t'        Dies ist die Eigenlänge der Rakete in System S’

in S:        t=\dfrac {t'}{\gamma}        Es wird die kürzere Zeit t gemessen.

Für die Länge der Rakete in System S gilt:

l=v\cdot t        Die in S gemessene Länge l ist aufgrund der Zeitdilatation gegenüber l' verkürzt (da t<t').

Der Beobachter in S misst also eine kleinere Länge als der Beobachter, der sich im Ruhesystem der Rakete (S’) befindet.

Aus der Zeitdilatation 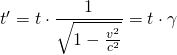 t'=t\cdot \dfrac {1}{\sqrt {1-\frac {v^{2}}{c^{2}}}}=t \cdot \gamma  ergibt sich für die in S gemessene Länge l:

l=l'\cdot \sqrt {1-\dfrac {v^{2}}{c^{2}}}=\dfrac {l'}{\gamma}

Die im Ruhesystem gemessene Länge eines Körpers wird auch als Eigenlänge bezeichnet. Sie ist stets größer als die in einem dazu bewegten System gemessene Länge des gleichen Körpers.

Der Effekt, dass die Länge eines Körpers, der sich relativ zum Beobachter bewegt, in Bewegungsrichtung verkürzt erscheint, wird als Längenkontraktion bezeichnet.

Längenkontraktion

Wenn sich ein Körper relativ zum Beobachter bewegt, so misst der Beobachter eine kürzere Länge als wenn sich der Körper relativ zum Beobachter in Ruhe befindet.

Die Länge l des relativ zum Beobachter bewegten Körpers ist gegenüber der Eigenlänge l' (Länge gemessen im Ruhesystem des Körpers) verkürzt und beträgt:

l=l'\cdot \sqrt {1-\dfrac {v^{2}}{c^{2}}}=\dfrac {l'}{\gamma}

Die Längenkontraktion ist wie die Zeitdilatation im Alltag nicht bemerkbar, da sich der Faktor \sqrt {1-\dfrac {v^{2}}{c^{2}}}=\dfrac {1}{\gamma} nur bei sehr hohen Geschwindkgkeiten v signifikant von 1 unterscheidet.

Mathematisch hatte schon H. A. Lorentz vor Ende des 19. Jahrhunderts die Längenkontraktion richtig vorhergesagt, allerdings mit anderer (falscher) Interpretation: Er vermutete, dass die Kontraktion durch die Kräfte des Ätherwindes auf die Moleküle zustande käme und erklärte so den negativen Ausgang des Michelson-Morley-Experiments.

Tatsächlich ist die Längenkontraktion jedoch nicht in dem Sinne real, dass ein bewegter Körper sich in Längsrichtung verformt. Vielmehr ist es so, dass Raum und Zeit andere Eigenschaften haben, als in der klassischen Physik zu Grunde gelegt. Diese Eigenschaften widersprechen unseren Alltagserfahrungen, weil wir sie im täglichen Leben nicht bemerken.

weiter mit Raum und Zeit
zurück