Auswertung der Ergebnisse aus der Gegenfeldmethode
Aus dem Diagramm der vorherigen Seite ergibt sich folgender Zusammenhang:
Die Energie der schnellsten Fotoelektronen steigt linear mit der Frequenz des eingestrahlten Lichts.
Es gibt jedoch keine direkte Proportionalität zwischen Frequenz und kinetischer Energie, da die Gerade nicht im Nullpunkt beginnt. Erst ab einer bestimmten Frequenz erhalten die Fotoelektronen kinetische Energie.
Trotzdem lassen sich aus dem Diagramm weitere Daten und Zusammenhänge entnehmen, die im folgenden Abschnitt erläutert werden.
Welche Erkenntnisse lassen sich aus dem Diagramm ableiten?
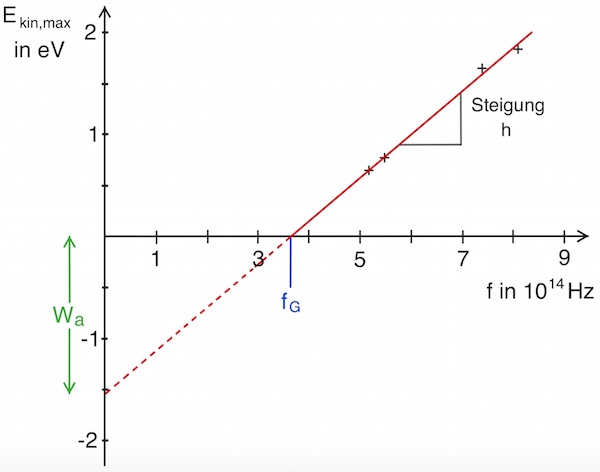
Zunächst verlängern wir die Gerade bis zur Energieachse. Da es natürlich keine negative kinetische Energie gibt, wird der verlängerte Abschnitt gestrichelt gezeichnet:
Im Diagramm wurden bereits einige Größen eingezeichnet, die im folgenden erläutert werden:
Die Steigung der Geraden
Die Steigung der Geraden ist unabhängig von der verwendeten Intensität und hängt auch nicht vom verwendeten Kathodenmaterial ab.
Es handelt sich um eine universelle Naturkonstante, die wir h nennen.
Die Steigung ergibt sich auf folgende Weise:
![]()
Mit Hilfe der Regressionsrechnung ergibt sich ein Wert von
h = 4,22 · 10-15 eVs bzw. h = 6,6 · 10-34 Js
Die Bedeutung dieser Steigung erkannte erst Albert Einstein – doch dazu später!
Grenzfrequenz
Im Schnittpunkt der Geraden mit der Frequenzachse lässt sich die Frequenz ablesen, ab der es überhaupt erst zum Fotoeffekt kommt. Bei dieser Frequenz können Elektronen herausgelöst werden, sie erhalten jedoch keine zusätzliche kinetische Energie.
Die Frequenz, ab der Elektronen aus dem Kathodenmaterial herausgelöst werden können, bezeichnet man als Grenzfrequenz fg. Unterhalb dieser Frequenz können keine Elektronen herausgelöst werden.
In unserem Beispiel beträgt die Grenzfrequenz fg = 3,65 · 1014 Hz.
Die entsprechende Wellenlänge heißt Grenzwellenlänge. Man erhält sie mit Hilfe der Grundgleichung zur Wellenausbreitung
![]()
Damit ergibt sich:
![]()
Diese Wellenlänge liegt knapp unterhalb der Wellenlängen sichtbaren Lichts, also im Infrarot-Bereich.
Ablösearbeit
Auch die Ablösearbeit WA lässt sich aus dem Diagramm entnehmen – sie entspricht dem Betrag der Energie, die man im Schnittpunkt der verlängerten Geraden mit der Energieachse ablesen kann.
In unserem Beispiel ergibt sich:
Die Ablösearbeit beträgt WA = 1,54 eV = 2,46 · 10-19 J.
Erhalten die Elektronen vom Licht weniger Energie, so können sie nicht herausgelöst werden, erhalten sie mehr Energie, so wird ein Teil dieser Energie in kinetische Energie umgewandelt.
Es lässt sich nun eine Geradengleichung aufstellen. Diese lautet:
Ekin, max = hf – WA
Diese Gleichung wird auch als Einstein-Gleichung bezeichnet.
Die Summe aus kinetischer Energie und Ablösearbeit entspricht also der gesamten von den Fotoelektronen aufgenommenen maximalen Energie. Diese ist proportional zur Frequenz des eingestrahlten Lichts.
Es lässt sich so auch schreiben:
hf = Ekin, max + WA
Wovon hängen Grenzfrequenz und Ablösearbeit ab?
Wir haben im ersten Versuch zum Fotoeffekt gesehen, dass es bei der Zinkplatte nur mit kurzwelligem UV-Licht möglich war, Elektronen herauszulösen. Bei der Fotozelle ist dies jedoch bereits ab einer Wellenlänge von ca. 820nm möglich.
Es wurde bereits erwähnt, dass die Steigung der Geraden immer gleich ist und weder von der Intensität des Lichts noch vom Kathodenmaterial abhängt. Demzufolge ergibt sich bei einer anderen Grenzfrequenz auch eine anderer Schnittpunkt mit der Energieachse und damit eine andere Ablösearbeit.
Ablösearbeit und Grenzfrequenz hängen von verwendeten Kathodenmaterial ab.
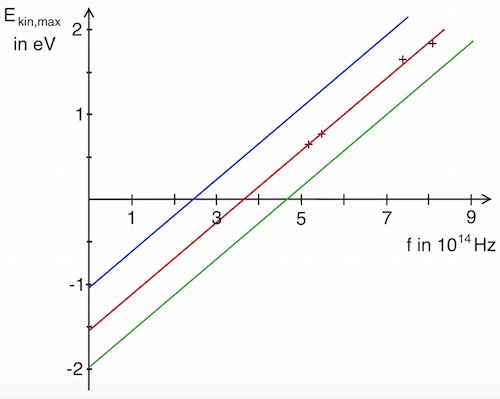
Im folgenden Diagramm sind zusätzlich die Ergebnisse des Versuchs für zwei andere Kathodenmaterialien dargestellt (blaue und grüne Gerade), aus dem sich Elektronen leichter (blau) bzw. schwerer (grün) herauslösen lassen – die Grenzfrequenz ist entsprechend unterschiedlich.