Herleitung der Bewegungsgleichung für harmonische Schwingungen
Um eine Funktion für die Auslenkung in Abhängigkeit von der Zeit zu finden, wird folgende Überlegung angestellt:
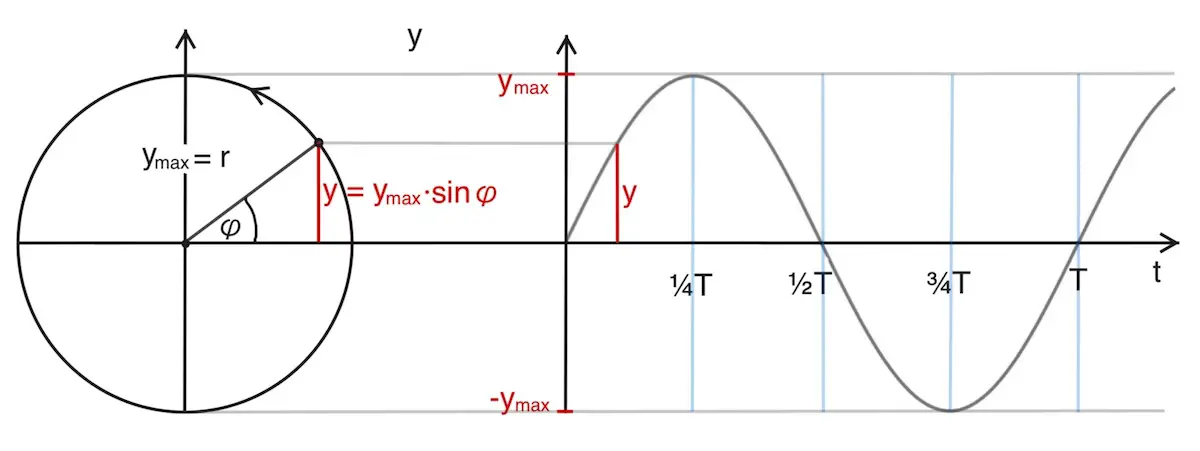
Die Projektion einer gleichförmigen Kreisbewegung entspricht der Bewegung eines harmonischen Oszillators.
Der Radius r entspricht dabei der Amplitude ymax, die Umlaufdauer entspricht der Schwingungsdauer T:
Für die Elongation y gilt jeweils:
![]()
Der Winkel ![]() , den man auch als Phasenwinkel oder Phase bezeichnet, lässt sich mit Hilfe der Umlaufzeit ausdrücken, denn es gilt:
, den man auch als Phasenwinkel oder Phase bezeichnet, lässt sich mit Hilfe der Umlaufzeit ausdrücken, denn es gilt:
![]() und damit
und damit ![]()
Dabei ist zu beachten, dass der Winkel ![]() im Bogenmaß angegeben wird.
im Bogenmaß angegeben wird.
Für einen gesamten Umlauf bzw. einen kompletten Schwingungsvorgang (also für die Periodendauer T) gilt: ![]() .
.
Der Quotient ![]() wird als Kreisfrequenz bzw. Winkelgeschwindigkeit
wird als Kreisfrequenz bzw. Winkelgeschwindigkeit ![]() bezeichnet:
bezeichnet:
![]()
Damit kann man für den Phasenwinkel ![]() auch schreiben:
auch schreiben:
![]()
Für den zeitlichen Verlauf der Auslenkung y gilt also:
![]()
Für eine gleichförmige Kreisbewegung ist die Kreisfrequenz ![]() konstant.
konstant.
Es gilt also ![]()
Wir haben damit also für eine harmonische Schwingung eine Funktion der der Auslenkung y in Abhängigkeit von der Zeit t gefunden. Sie lautet:
![]() bzw.
bzw. ![]()
(Die Klammer ist nicht notwendig, soll aber hier verdeutlichen, dass der Sinus von ![]() gemeint ist und nicht (
gemeint ist und nicht (![]() .)
.)
Diese Funktion wird als Gleichung für harmonische Schwingungen bezeichnet. Sie lässt sich auch mit Hilfe der Schwingungsdauer T oder der Frequenz f ausdrücken.
Dazu ersetzt man die Kreisfrequenz wieder durch ![]() bzw.
bzw. ![]()