Nach unserer (klassischen) Vorstellung ist es möglich, dass man jedem Objekt einen genauen Ort sowie eine Masse und Geschwindigkeit und damit einen eindeutigen Impuls zuweisen kann.
Tatsächlich ist das jedoch nicht beliebig genau möglich – je genauer die eine Größe (der Ort) bestimmt wird, umso ungenauer lässt sich die andere Größe (der Impuls) bestimmen.
Beeinflusst die Messung das Verhalten der Elektronen?
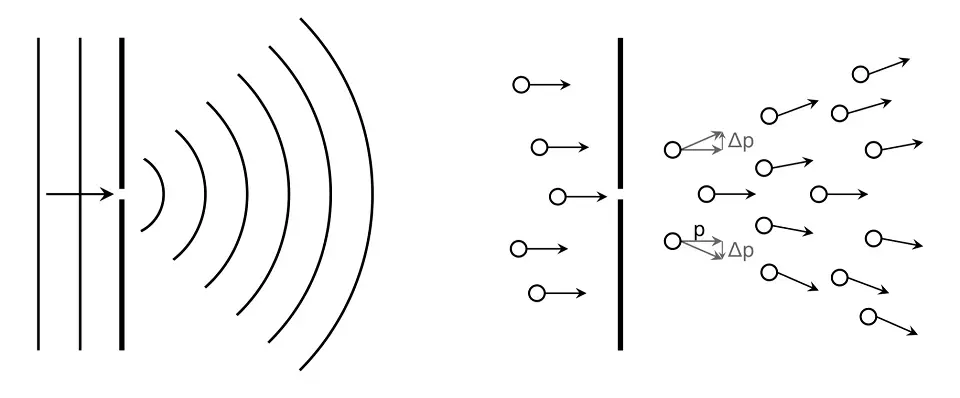
Bei der Ortsmessung der Elektronen beim Doppelspaltexperiment könnte man damit argumentieren, dass die Photonen, mit denen der Ort der Elektronen bestimmt wird, einen Impuls auf die Elektronen übertragen und diese damit beeinflussen, wodurch sich ihr Impuls ändert.
Bei einer kleineren Wellenlänge des Lichts, kann der Ort zwar genauer bestimmt werden, allerdings besitzen die Photonen dann einen größeren Impuls und beeinflussen die Elektronen stärker, so dass sie von ihrem Verhalten ohne Ortsmessung noch weiter abweichen.
Heisenberg’sche Unbestimmtheitsrelation
Tatsächlich handelt es sich aber um ein grundlegendes Prinzip, dass nichts mit dem Messvorgang an sich oder mit der Messmethode zu tun hat:
Es ist prinzipiell nicht möglich, Ort und Impuls eines Objektes gleichzeitig beliebig genau zu bestimmen. Diese Tatsache wurde 1927 von Werner Heisenberg formuliert und wird als Heisenberg’sche Unbestimmtheitsrelation oder Heisenberg’sche Unschärferelation bezeichnet.
Diese Unbestimmtheit tritt bei vielen messbaren Größen in der Quantenphysik auf.
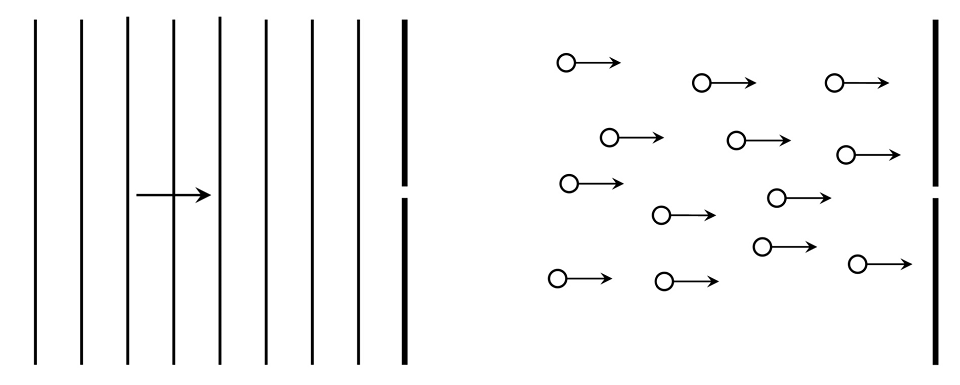
Auch das Prinzip der Beugung lässt sich mit der Unbestimmtheitsrelation erfassen
Um mit einem Laserstrahl eine Nadelspitze zu beleuchten, kann man den Laser vor einen Spalt stellen und diesen immer weiter einengen.
Dadurch wird das Lichtbündel zunächst schmaler, doch sobald die Wellenlänge nicht mehr vernachlässigbar klein gegenüber dem Blendendurchmesser ist, tritt Beugung auf, und das Lichtbündel wird wieder breiter.
Diese Beugungserscheinungen treten bei allen Quantenobjekten, also auch bei Elektronen, auf.
Das bedeutet:
Ein Elektron bewegt sich nicht auf beliebig dünnen Linien!
Der Aufenthaltswahrscheinlichkeitsbereich ist einige De-Broglie-Wellenlängen breit.
Der „Bahn“-begriff ist also problematisch – letztendlich bedeutet das:
Quantenobjekte bewegen sich nicht auf Bahnen.
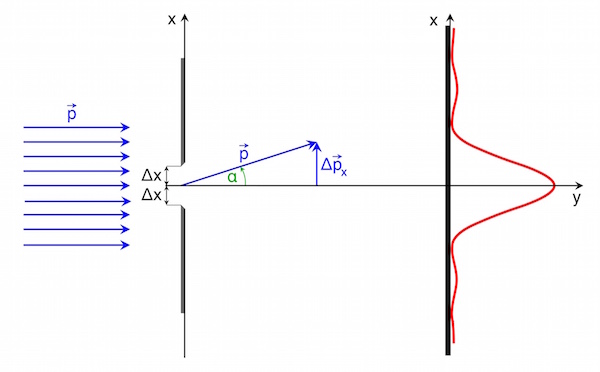
Solange man den Aufenthaltsbereich für ein Quantenobjekt nicht stark einschränkt, spielen diese Effekte keine Rolle. Je schmaler allerdings der Spalt wird, umso stärker wird der Aufenthaltsort eingeschränkt und umso „unschärfer“ wird der Impuls (genauere Erklärung dazu s.u.).
Aber z.B. in Atomen, in denen Elektronen in einem Bereich mit einem Durchmesser von etwa 10-10 m „eingesperrt“ sind, ist es unmöglich, für diese eine Bahn anzugeben.
Dies ist ein entscheidender Unterschied zwischen der Newton’schen Mechanik und der Quantenmechanik. Die Quantenmechanik spielt daher eine ebenso wichtige Rolle in der Atomphysik (Quantenphysik der Atomhülle).