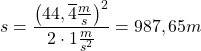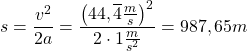Physikaufgaben lösen

Bei der Bearbeitung von Physikaufgaben – sei es in einer Klassenarbeit oder Klausur, als Hausaufgabe oder als Übung in der Schule – treten immer wieder ganz bestimmte Fehler, Schwierigkeiten oder Nachlässigkeiten auf. Viele Probleme sind nicht themenbezogen sondern auf grundlegende fehlerhafte oder nachlässige Herangehensweise zurückzuführen. Hat man die richtige Vorgehensweise einmal verinnerlicht, kann man eine Reihe von Fehlern praktisch von vornherein ausschließen.

Voraussetzung für erfolgreiches Bearbeiten von Aufgaben

Für die korrekte Bearbeitung von Physikaufgaben werden bestimmte Basiskenntnisse und -fertigkeiten vorausgesetzt, und zwar der sichere Umgang mit

Grundregeln zum Lösen von Aufgaben

Die Vorgehensweise beim Lösen von Physikaufgaben ist im Grunde immer gleich und lässt sich auf fast alle Arten von Aufgaben anwenden. Leider werden schon bei der Herangehensweise immer wieder bestimmte Fehler gemacht, die das Lösen von Aufgaben erschweren oder sogar verhindern.

Viele Fehler lassen sich ganz einfach vermeiden, indem man sich an bestimmte Grundregeln hält.

Zu diesen Grundregeln gehören:

Alle gegebenen Werte werden (falls nicht bereits angegeben) in die Basiseinheiten umgerechnet. Beachte: Die Basiseinheit der Masse ist Kilogramm (kg) und nicht Gramm (g)!

Formeln werden in korrekter Schreibweise geschrieben. Divisionen werden immer als Bruch geschrieben. Das Zeichen „:“ hat in einer physikalischen Formel nichts zu suchen! Doppelbrüche können und sollten immer vermieden werden.

Es werden stets alle Einheiten mitgeschrieben.

Es muss der vollständige Lösungsweg erkennbar sein. Eingesetzte Werte werden aufgeschrieben.

(Fehlen die eingesetzten Werte, und das Ergebnis ist richtig, gibt es in vielen Fällen keinen Punktabzug. Bei falschen Ergebnis können jedoch keine Teilpunkte für richtig eingesetzte Werte vergeben werden! Außerdem ist eine nachträgliche Kontrolle kaum möglich, wenn man nicht mehr weiß, wie man auf das Ergebnis gekommen ist.)

Vorgehensweise am Beispiel

Die Vorgehensweise beim Lösen einer Physikaufgabe soll nun ausführlich an einem einfachen Beispiel erläutert werden.

Beispielaufgabe

Ein Zug beschleunigt innerhalb einer Minute aus der Ruhe auf eine Geschwindigkeit von 160km/h.

a) Berechne die mittlere Beschleunigung des Zuges!

b) Welcher Weg wird während der Beschleunigung zurückgelegt?

c) Wie lang wäre der Beschleunigungsweg bei einer Beschleunigung von a = 1m/s²?

d) Der Zug wird (gleichmäßig) mit a = -1,8m/s² abgebremst. Wie lange dauert der Bremsvorgang?

Es soll nun die Herangehensweise Schritt für Schritt erläutert werden.

Erster Schritt: Zusammenfassung aller gegebenen Größen in den Basiseinheiten

Zeit 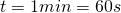$t=1min=60s$

Geschwindigkeit 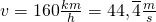$v=160 \frac {km}{h}=44,\overline {4}\frac {m}{s}$

Nun lösen wir nacheinander die einzelnen Aufgabenteile:

Aufgabenteil a)

Vorüberlegung:

Die gesuchte Größe ist die Beschleunigung a. Die Beschleunigung ist definiert als Geschwindigkeitsänderung pro Zeit.

In der Formelsammlung findet man daher die Definition 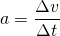$a=\dfrac {\Delta v}{\Delta t}$ .

Sowohl die Geschwindigkeit(sänderung) als auch die dafür benötigte Zeit sind gegeben, also können wir diese in die Definition der Beschleunigung einsetzen:

1. Benötigte Formel für zu berechnender Größe (hier: a) hinschreiben:

$a=\dfrac {\Delta v}{\Delta t}$

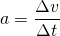
2. Werte (in Basiseinheiten!) einsetzen und Ergebnis hinschreiben:

$a=\dfrac {44,\overline {4}\frac {m}{s}}{60s}=0,74\dfrac {m}{s^{2}}$ .

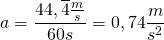Beachte: Alle Einheiten in der Formel werden mitgeschrieben. Noch wichtiger ist die Einheit beim Ergebnis. Ein Ergebnis ohne Einheit ist unbrauchbar!

Merke: Setzt man die Basiseinheiten in die Formel ein, kommt auch immer die Basiseinheit heraus! Die einzig sinnvolle Einheit der Beschleunigung lautet 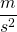$\dfrac {m}{s^{2}}$ !

Immer genaue Werte einsetzen!

Bei der Umrechnung der Geschwindigkeit in m/s erhält man u.U. einen Wert mit unendlich vielen Nachkommastellen (in diesem Beispiel ein Zahlenwert mit Periode). Beim Einsetzen schreibt man den gerundeten Wert hin, gerechnet wird aber mit dem genauen Wert. Erst beim Endergebnis wird wieder gerundet (in der Regel zwei Stellen nach dem Komma, wenn vor dem Komme keine Null steht).

3. Antwortsatz (je nach Vorgaben) nicht vergessen:

Die mittlere Beschleunigung des Zuges beträgt 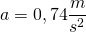$a=0,74\dfrac {m}{s^{2}}$ .

Aufgabenteil b)

Vorüberlegung:

Nun wird der Weg bzw. die Strecke s gesucht, die während der Beschleunigung zurückgelegt wird.

Das Weg-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung lautet: 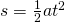$s=\frac {1}{2}at^{2}$ .

Wir können direkt die benötigten Werte in diese Formel einsetzen und erhalten:

$s=\frac {1}{2}\cdot 0,74 \dfrac {m}{s^{2}}\cdot (60s)^{2}=1333,33m$

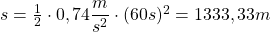
Auch hier sollte der vorher berechnete genaue Wert für die Beschleunigung eingesetzt werden. Die Zeit muss die Einheit Sekunden haben. Beachte die korrekte Schreibweise: Die Zeit mit Einheit wird eingeklammert, das Quadrat gilt für den Zahlenwert und die Einheit!

Antwortsatz: Der Beschleunigungsweg beträgt 1.333.33m.

Aufgabenteil c)

Nun ist die Beschleunigungszeit t nicht bekannt. Um den Weg berechnen zu können, muss die unbekannte Größe durch einen bekannten Zusammenhang ersetzt werden.

Wir erinnern uns an das Geschwindigkeits-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung (die nach v umgestellte Definition der Beschleunigung). Es lautet: 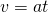$v=at$ .

Diese Formel lässt sich nach t umstellen und in das Weg-Zeit-Gesetz einsetzen. Die formulierte Lösung lautet also:

Es gilt: 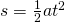$s=\frac {1}{2}at^{2}$

Außerdem gilt: 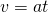$v=at$ $\Leftrightarrow$ $t=\dfrac {v}{a}$

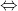
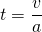
Einsetzen liefert:

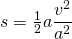$s=\frac {1}{2}a\dfrac {v^{2}}{a{^2}}$ a lässt sich kürzen, und wir schreiben die “2” unter den Bruchstrich:

$s=\dfrac {v^{2}}{2a}$

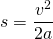
Nun werden die Werte eingesetzt:

$s=\dfrac {\left( 44,\overline {4}\frac {m}{s}\right) ^{2}}{2\cdot 1\frac {m}{s^{2}}}=987,65m$

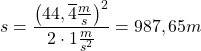
Hinweis: Für die Geschwindigkeit wird wieder der genaue (nicht gerundete) Werte eingesetzt.

Beachte außerdem die korrekte Schreibweise von 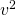$v^{2}$ : Der Zahlenwert mit Einheit steht in der Klammer, beides wird quadriert!

Antwortsatz: Der Beschleunigungsweg beträgt 987,65m.

Hinweis: Eine andere Möglichkeit wäre gewesen, zunächst mit Hilfe des Geschwindigkeits-Zeit-Gesetzes die Beschleunigungszeit t zu berechnen und diese anschließend in das Weg-Zeit-Gesetz einzusetzen. Der hier gezeigte Weg ist jedoch ein wenig eleganter und sollte Dir in jedem Fall bekannt sein. Das Ersetzen einer Größe durch einen bekannten Zusammenhang ist eine wichtige Grundfertigkeit, die Du beherrschen solltest.

Aufgabenteil d)

Nun wird die Zeit t gesucht, in der der Zug zum Stehen kommt.

Die Bremsbeschleunigung beträgt 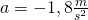$a=-1,8\frac {m}{s^{2}}$ .

Für die Zeit gilt (s.o.): 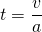$t=\dfrac {v}{a}$

Nun werden die Werte eingesetzt:

$t=\dfrac {44,\overline {4}\frac {m}{s}}{1,8\frac {m}{s^{2}}}=24,69s$

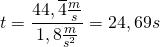
[Das negative Vorzeichen wurde hier weggelassen, da die Zeit natürlich nicht negativ sein kann. Mathematisch korrekt wäre es, auch der Geschwindigkeit ein negatives Vorzeichen zuzuschreiben, weil die Geschwindigkeitsänderung bei einem Bremsvorgang negativ ist – die Geschwindigkeit wird kleiner!]

Antwort: Der Bremsvorgang dauert knapp 25 Sekunden.

Kontrolle:

Nach der Bearbeitung jedes Aufgabenteils macht es Sinn, das Ergebnis auf Plausibilität zu überprüfen. In vielen Fällen kann man zumindest die Größenordnung des Ergebnisses bereits vor der Rechnung abschätzen. So ist die Beschleunigung des Zuges sicherlich deutlich kleiner als die Erdbeschleunigung (g = 9,81m/s²).

Liegt das Ergebnis außerhalb der abgeschätzten Größenordnung, sollte man die Rechnung noch einmal überprüfen – vielleicht hat man Nenner und Zähler vertauscht, eine Null vergessen, vergessen eine Größe zu quadrieren etc.

Derartige Fehler lassen sich meist leicht finden, wenn man danach sucht. Durch Einhaltung der Grundregeln lassen sie sich meist jedoch von vornherein vermeiden.

Näheres zur Kontrolle findest Du weiter unten.

Musterlösung

Es folgt noch einmal eine Musterlösung ohne Kommentare in kompakter Form, wie sie in einer Klausur ausreichend wäre:

a) Für die Beschleunigung gilt: $a=\dfrac {\Delta v}{\Delta t} =\dfrac {44,\overline {4}\frac {m}{s}}{60s}=0,74\dfrac {m}{s^{2}}$

Die Beschleunigung beträgt $a=0,74\dfrac {m}{s^{2}}$ .

b) Es gilt: $s=\frac {1}{2}at^{2}=\frac {1}{2}\cdot 0,74 \dfrac {m}{s^{2}}\cdot (60s)^{2}=1333,33m$

Der zurückgelegte Weg beträgt $s = 1333,33m$ .

c) Es gilt: $s=\frac {1}{2}at^{2}$

Außerdem gilt: $v=at$ $\Leftrightarrow$ $t=\dfrac {v}{a}$

Damit ergibt sich: $s=\dfrac {v^{2}}{2a}=\dfrac {\left( 44,\overline {4}\frac {m}{s}\right) ^{2}}{2\cdot 1\frac {m}{s^{2}}}=987,65m$

Der Beschleunigungsweg beträgt $s=987,65m$ .

d) Es gilt (s.o.): $t=\dfrac {v}{a}=\dfrac {44,\overline {4}\frac {m}{s}}{1,8\frac {m}{s^{2}}}=24,69s$

Der Bremsvorgang dauert knapp 24,7 Sekunden.

Grundsätze zum Lösen von Physikaufgaben

Hält man sich an bestimmte Grundsätze und Vorgehensweisen, so lassen sich viele Fehler vermeiden, und viele Schwierigkeiten kommen erst gar nicht auf.

Die folgende Übersicht enthält noch einmal die korrekte Vorgehensweise sowie alle wichtigen Grundsätze, die Du bei der Bearbeitung jeder Physikaufgabe einhalten solltest. Am besten druckst Du sie Dir aus und klebst Sie in Dein Heft, bis sie für Dich selbstverständlich geworden sind!

Vorgehensweise und Grundsätze zur Bearbeitung von Physikaufgaben

Gegebene Größen erfassen und in Basiseinheiten umrechnen

Gesuchte Größe(n) erfassen und Zusammenhang (Formel) aufstellen

Formel zur gesuchten Größe hin umstellen (korrekte Schreibweise beachten!). Das Umstellen von Formeln ist eine der wichtigsten Grundfertigkeiten im Physikunterricht!

Erst nach dem Umstellen der Formeln Werte (in Basiseinheiten!) einsetzen. Einheiten nicht vergessen!

Ergebnis (mit Einheit!) aufschreiben und deutlich als Ergebnis kennzeichnen (z.B. doppelt unterstreichen)

Ggf. in andere Einheit (je nach Vorgabe) umrechnen oder mit Vorsilbe aufschreiben

Ggf. Antwortsatz aufschreiben. Dabei präzise Formulierung und korrekte Fachsprache verwenden

Kontrolle: Habe ich alle Aufgabenteile bearbeitet? Ist das Ergebnis realistisch?* (ansonsten noch einmal überprüfen!)

* Kontrolle:

1) Ergebnisse abschätzen und überprüfen

Wie in der Beispielaufgabe bereits beschrieben wurde, kann man in vielen Aufgaben das Ergebnis abschätzen, zumindest die Größenordnung ist oft vorhersehbar. Hier einige Beispiele:

Ist nach der Geschwindigkeit eines Radfahrers gefragt, wird diese sicher nicht in der Nähe der Lichtgeschwindigkeit sein.

Eine elektrische Feldstärke in der Größenordnung von 10^-12V/m sollte einen stutzig machen. Elektrische Feldstärken liegen meist in einer Größenordnung von 10⁵V/m.

Erhält man für sichtbares Licht eine Wellenlänge von 10⁹m, so hat man definitiv einen Fehler gemacht, denn sichtbares Licht hat eine Wellenlänge zwischen ca. 400 und 800nm (also zwischen 4·10^-7m und 8·10^-7m).

Soll eine physikalische Konstante z.B. aus Messergebnissen ermittelt werden, so kennt man das Ergebnis bereits – Die Konstante lässt sich in der Formelsammlung nachschlagen, oder man hat den Wert noch in Erinnerung. Die korrekte Berechnung ergibt sicherlich nicht genau den Literaturwert, wird diesem aber sehr nahe sein.

Es gibt zahlreiche weitere Beispiele für eine einfache Abschätzung des Ergebnisses.

In vielen Fällen ist der Grund für eine völlig falsche Größenordnung nur ein kleiner Fehler, der sich einfach finden lässt, wenn man gezielt danach sucht.

Falls der trotzdem nicht zu finden ist, sollte als Kommentar zum Ergebnis zumindest eine Bemerkung wie „Wert erscheint viel zu hoch / zu niedrig“, möglichst mit Begründung, dabei stehen.

2) Alle Aufgabenteile bearbeitet?

So banal es sich anhört – sehr häufig werden Aufgabenteile, wie z.B. die Berechnung einer bestimmten Größe, einfach vergessen. Das kann jedem passieren, und deshalb solltest Du nach der Bearbeitung einer Aufgabe kurz kontrollieren, ob Du wirklich alle Fragen beantwortet und alle gesuchten Größen berechnet hast.

Nichts ist ärgerlicher, als Punkte zu verlieren, obwohl man die Aufgabe leicht hätte lösen können.

Häufige Fehler

Zum Abschluss noch einmal eine Auflistung der häufigsten Fehler bei der Bearbeitung von Physikaufgaben. Auch diese Checkliste solltest Du immer dabei haben, bis Du sie verinnerlicht hast:

Einheiten nicht in Basiseinheiten umgerechnet

Einheiten nicht mitgeschrieben

Formeln falsch umgestellt

Formeln unübersichtlich oder fehlerhaft aufgeschrieben

Quadrieren oder Wurzel ziehen vergessen (resultiert oft aus unübersichtlicher Formel bzw. fehlerhafter Schreibweise)

Ansatz fehlt / Formel nicht aufgeschrieben *

Eingesetzte Werte nicht aufgeschrieben

Ergebnis nicht hinterfragt

* Auch wenn Du zunächst keine Idee hast, wie die Aufgabe zu lösen ist – in den meisten Fällen gibt es bereits Punkte für den richtigen Ansatz / die richtige Idee oder die passende Formel. Hat man erst einmal einen Ansatz aufgeschrieben, fällt es außerdem leichter, den nächsten Schritt zur Lösung zu finden.

Es lohnt sich in jedem Fall, einmal etwas Zeit in das Aneignen und Vertiefen der hier beschriebenen Grundsätze zu investieren.

Hast Du diese verinnerlicht, wirst Du wesentlich entspannter an Physikaufgaben herangehen – sei es bei Hausaufgaben oder in der Klausur! Du wirst weniger Fehler machen und mehr Erfolgserlebnisse haben!

zurück zu Hilfsmittel