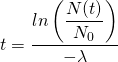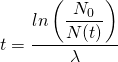Formeln umstellen, um Größen zu berechnen

Physikalische Zusammenhänge werden meist mit Hilfe von Gleichungen (Formeln) dargestellt. Eine physikalische Formel stellt den Zusammenhang zwischen verschiedenen physikalischen Größen dar. Soll eine dieser Größen berechnet werden, müssen die anderen bekannt sein. Eine Formel umstellen bedeutet, eine solche Gleichung so umzuformen, dass eine bestimmte Größe berechnet werden kann.


Formel umstellen Physik

Formeln umstellen führt immer wieder zu Problemen – das muss nicht sein!


Formeln umstellen – die wichtigste Voraussetzung zum Lösen von Physikaufgaben

Eine der wichtigsten Voraussetzungen für das erfolgreiche Lösen von Physikaufgaben ist die Fähigkeit, Gleichungen (Formeln) so umzuformen bzw. umzustellen, so dass die gesuchte Größe allein auf einer Seite steht. Es gibt kaum eine Physikaufgabe, in der man nicht mindestens eine Formel umstellen muss. Leider stellt das Formeln umstellen jedoch für viele Schüler – selbst in der Oberstufe – eine mehr oder weniger große Schwierigkeit dar.

Schwierigkeiten beim Umstellen von physikalischen Formeln haben zur Folge, dass man kaum eine Aufgabe sicher lösen kann, was zu Frustration und manchmal sogar zur Resignation führt. Aussagen wie “das habe ich noch nie verstanden” oder “das lerne ich nie” hört man in diesem Zusammenhang immer wieder.

Doch glaube mir bitte: Formeln umstellen kann jeder lernen, und es ist eigentlich ganz einfach!

Wenn man ersteinmal verstanden hat, wie es geht, und gemerkt hat, dass das Formeln umstellen meist ganz einfach ist, dann führt das nicht nur schlagartig zu besseren Leistungen sondern auch zu mehr Spaß und Motivation im Physikunterricht.

Es gibt kaum ein weiteres Beispiel in der Schule, wie man sich durch das Aneignen bzw. durch das Festigen einer einzigen Fähigkeit in einem Fach so schnell, so deutlich und so nachhaltig verbessern kann.

Was ist eine Gleichung?

Jede physikalische Formel hat die Form einer Gleichung. Hier ein paar Beispiele:

F=m\cdot a     (Grundgleichung der Mechanik)

v=\dfrac {s}{t}     (Geschwindigkeit einer gleichförmigen Bewegung)

s=\frac {1}{2}a\cdot t^{2}     (Weg-Zeit-Gesetz einer gleichmäßig beschleunigten Bewegung)

oder ein wenig komplizierter

E_{ges,n}=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}

(Gesamtenergie eines Elektrons auf der n-ten Bahn im Bohrschen Atommodell)

Jede Gleichung besteht aus zwei Seiten und einem Gleichheitszeichen dazwischen.

Das Gleichheitszeichen besagt, dass auf beiden Seiten das Gleiche steht – auch wenn es völlig anders aussieht.

Es ist möglich, jede Gleichung zu verändern, indem man etwas hinzuaddiert, subtrahiert oder eine beliebige andere Rechenoperation durchführt. Doch damit die Gleichung erfüllt bleibt, also noch immer auf beiden Seiten das Gleiche steht, muss man jede Rechenoperation immer gleichermaßen auf beiden Seiten durchführen.

Merke:

Damit die Gleichung erfüllt bleibt, musst Du auf beiden Seiten der Gleichung immer das gleiche tun.

Dazu ein paar Beispiele:

Beispiel 1

Wir beginnen zunächst mit einer einfachen Gleichung ohne physikalische Größen. Das Umstellen solcher Gleichungen kennst Du sicher aus dem Mathematikunterricht:

2x+5=11

Wir wollen diese Gleichung nun so umstellen, dass wir “x“ berechnen können. Dazu muss “x” alleine auf einer Seite stehen. Wir suchen also eine Gleichung in der Form “x=…”.

Damit “x” alleine auf einer Seite steht, müssen wir die anderen Größen bzw. Zahlen auf dieser Seite loswerden.

Hinweis: Die Schreibweise “2x” ist gleichbedeutend mit “2\cdot x“. Auch in physikalischen Formeln wird das Multiplikationszeichen meist weggelassen.

Schritt 1

Wir wollen zunächst auf der linken Seite die “5” loswerden. Da in der Gleichung “+ 5” steht, müssen wir diese “5” subtrahieren, denn 5 – 5 = 0 – womit die “5” wegfällt. Damit die Gleichung erfüllt bleibt, müssen wir dies auch auf der rechten Seite tun.

Wir subtrahieren also auf beiden Seiten die Zahl “5”.

Alle Rechenoperationen werden hinter einem Betragsstrich hinter die Gleichung geschrieben:

2x+5=11          \vert -5

Auf der linken Seite fällt die “5” weg, für die rechte Seite gilt: 11-5=6.

Die Gleichung lautet also nun

2x=6

Schritt 2

Da wir nicht “2x” suchen, sondern “x” , müssen wir die Gleichung (also beide Seiten) schließlich noch durch “2” teilen:

2x=6     \vert :2

Das Ergebnis liefert den gesuchten Wert für “x” :

x=3

Die gesuchte Größe muss freigestellt werden

In jeder Gleichung ist die gesuchte Größe mit einer anderen Größe oder Zahl verknüpft. Im oberen Beispiel ist das “x” durch Multiplikation mit der “2” und durch Addition mit der “5” verknüpft.

Um eine Bindung aufzulösen, muss jeweils die Umkehroperation (oder Gegenoperation) durchgeführt werden.

Die Umkehroperation der Multiplikation ist die Division, die Umkehroperation zur Addition ist die Subtraktion.

Mathematische Verknüpfungen sind unterschiedlich stark. Die schwächsten mathematischen Verknüpfungen sind die Addition und Subtraktion (+ / -), gefolgt von der Multiplikation und Division (· / :).

Hier eine Übersicht verschiedener Umkehroperationen in der Reihenfolge der Stärke der Verknüpfungen:

Operation Symbol Gegenoperation Symbol
Addition + Subtraktion -
Multiplikation \cdot Division :
Quadratwurzel \sqrt{} Quadrat (\;)^{2}
n-te Wurzel \sqrt [n] {} Potenz (\;)^{n}
e-Funktion e^{x} natürlicher Logarithmus ln(x)

Operation und Gegenoperation sind jeweils austauschbar.

In der Regel wird immer zuerst die momentan schwächste Bindung mit der entsprechenden Umkehroperation aufgelöst und nachfolgend die stärkeren.

Genauso sind wir auch in Beispiel 1 oben vorgegangen.

Beispiel 2

Nun machen wir das gleiche mit einer physikalischen Formel:

Wir wollen die Formel  F=m\cdot a  (s.o.) so umstellen, dass wir die Masse m bei bekannter Kraft F und bekannter Beschleunigung a berechnen können. Dazu muss die Masse m alleine auf einer Seite stehen.

Wir suchen also eine Gleichung in der Form  “m= …”

Damit die Masse m alleine auf einer Seite steht, müssen wir die anderen Größe(n) auf dieser Seite (in diesem Fall nur die Beschleunigung a ) loswerden.

Auf der rechten Seite steht das Produkt aus Masse m und Beschleunigung a. Wir müssen also die Gleichung (und damit beide Seiten) durch die Beschleunigung a teilen (dividieren):

F=m\cdot a     bzw.     F=ma          \vert :a

Das Ergebnis lautet:

\dfrac {F}{a}=\dfrac {m\cdot a}{a}

Nun kann man auf der rechten Seite einfach kürzen, so dass die Beschleunigung wegfällt, denn es gilt:

\dfrac {a}{a}=1        und damit        \dfrac {m\cdot a}{a}=m

Mit ein wenig Routine kannst Du diesen Zwischenschritt natürlich weglassen und gleich das Ergebnis nach der durchgeführten Rechenoperation hinschreiben. Wir werden das in den nachfolgenden Beispielen auch tun.

Am Ende kann man die beiden Seiten nun noch einfach vertauschen, so dass wir schreiben können:

m=\dfrac {F}{a}

Wir haben nun die Gleichung nach m umgestellt. Nun ließen sich Werte für die Kraft F und Beschleunigung a einsetzen und damit die Masse m berechnen.

Beispiel 3

Wir wollen nun die eben umgeformte Gleichung ein weiteres Mal so umformen, dass wir die Beschleunigung a berechnen könnten, also dass “a” alleine auf einer Seite steht.

Zu beachten ist dabei, dass die gesuchte Größe nun im Nenner steht:

m=\dfrac {F}{a}

Wichtiger Grundsatz beim Formeln umstellen:

Steht die gesuchte Größe im Nenner, dann multipliziere die Gleichung mit dieser Größe!

Wir multiplizieren also die Gleichung mit “a“:

m=\dfrac {F}{a}          \vert \cdot a

Damit erhalten wir die Gleichung wieder in der Grundform

ma=F     bzw.     F=ma

Nun müssen wir die Gleichung noch durch “m” dividieren:

F=ma          \vert :m

Wenn wir dann noch die beiden Seiten vertauschen, erhalten wir so für die Beschleunigung a:

a=\dfrac {F}{m}

Achtung: Ein sehr häufiger Fehler ist folgender:

Du schaust Dir die Gleichung  m=\dfrac {F}{a}   bzw.   \dfrac {F}{a}=m   an und denkst vielleicht:

“Auf der linken Seite will ich die Kraft F loswerden, also dividiere ich durch “F“:

\dfrac {F}{a}=m         \vert :F

Doch Vorsicht: Die Gleichung lautet nun nicht   a=\dfrac {m}{F} !

Die Beschleunigung a steht noch immer im Nenner, also müssten wir schreiben:

\dfrac {1}{a}=\dfrac {m}{F}

Um die Gleichung nach “a” umzustellen, müsste nun auf beiden Seiten der Kehrwert gebildet werden. Damit erhält man

a=\dfrac {F}{m}

und damit das gleiche Ergebnis wie oben.

Beachte also immer den oben genanten Grundsatz, und teile nie durch die gesuchte Größe!

Auch kompliziertere Formeln lassen sich einfach umformen

Beachtet man das einfache Prinzip, dass immer auf beiden Seiten die gleichen Operationen durchgeführt werden müssen, so lassen sich auch komplizierte Formeln (ohne dass man dafür übrigens die Größen oder den Zusammenhang kennen oder verstehen muss!) ganz einfach zu jeder beliebigen Größe umstellen.

Wir wollen nun die letzte Gleichung aus den o.g. Beispielen umstellen:

E_{ges,n}=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}

Ohne dass wir die Gleichung verstehen oder wissen müssen, welche Bedeutung die einzelnen Symbole haben, können wir sie trotzdem zu jeder beliebigen Größe hin umstellen:

Umstellen nach me

Wir wollen die Gleichung zunächst nach m_{e} (Elektronenmasse) umstellen. Dazu müssen wir zunächst den Bruch loswerden, indem wir einfach die gesamte Gleichung mit dem Nenner auf der rechten Seite multiplizieren:

E_{ges,n}=-\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}          \vert \cdot8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}

Wir tauschen noch linke und rechte Seite und erhalten damit

-m_{e}e^{4}=E_{ges,n}\cdot8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}

oder etwas anders geschrieben

-m_{e}e^{4}=8E_{ges,n}\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}

Hinweis: Die Klammer bei \left(\varepsilon_{0}\right)^{2} ist nicht notwendig sondern dient nur der Klarheit.

Als nächstes können wir das negative Vorzeichen loswerden, indem wir die Gleichung mit (-1) multiplizieren. Dadurch wechselt auf beiden Seiten das Vorzeichen, und wir erhalten

m_{e}e^{4}=-8E_{ges,n}\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}          \vert :e^{4}

Der nächste und letzte Schritt, nämlich die Division durch e^{4}, ist dann offensichtlich.

Die nach m_{e} umgestellte Gleichung lautet schließlich

m_{e}=-\dfrac {8E_{ges,n}\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}{e^{4}}

Umstellen nach h

Nun wollen wir die Ausgangsgleichung nach h (Planck’sche Konstante) umstellen. Der Einfachheit halber lassen wir das negative Vorzeichen weg (die Bedeutung spielt hier keine Rolle und soll hier nicht erläutert werden).

Da die gesuchte Größe h bzw. h^{2} im Nenner steht, müssen wir zunächst die Gleichung (also beide Seiten!) mit h^{2} multiplizieren (s. Grundsatz!):

E_{ges,n}=\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}h^{2}n^{2}}          \vert \cdot h^{2}

Dadurch steht h^{2} als Produkt auf der linken Seite und fällt auf der rechten Seite weg. Wir erhalten die Gleichung

E_{ges,n}\cdot h^{2}=\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}n^{2}}

Nun können wir die Energie E_{ges,n} auf der linken Seite loswerden, indem wir durch diese dividieren:

E_{ges,n}\cdot h^{2}=\dfrac {m_{e}e^{4}}{8\left(\varepsilon_{0}\right)^{2}n^{2}}          \vert :E_{ges,n}

Dadurch steht die Energie auf der rechten Seite unter dem Bruchstrich, und wir erhalten

h^{2}=\dfrac {m_{e}e^{4}}{8E_{ges,n}\left(\varepsilon_{0}\right)^{2}n^{2}}          \vert \sqrt{}

Um aus h^{2} die gesuchte Größe h zu erhalten, müssen wir schließlich noch die Wurzel ziehen – und zwar sowohl von der linken Seite als auch von der gesamten rechten Seite. So erhalten wir schließlich für h:

h=\sqrt {\dfrac {m_{e}e^{4}}{8E_{ges,n}\left(\varepsilon_{0}\right)^{2}n^{2}}}

Da einige Größen als Quadrat unter der Wurzel stehen, könnte man diese noch aus der Wurzel ziehen und davor schreiben:

h=\dfrac {e^{2}}{\varepsilon_{0}n}\cdot \sqrt {\dfrac {m_{e}}{8E_{ges,n}}}     oder (da 8 = 2 · 4)     h=\dfrac {e^{2}}{2\varepsilon_{0}n}\cdot \sqrt {\dfrac {m_{e}}{2E_{ges,n}}}

Schritt für Schritt zur gesuchten Gleichung

Auch wenn es auf den ersten Blick ein wenig kompliziert erscheint – jeder einzelne Schritt erfordert keine besonderen mathematischen Fähigkeiten. Außerdem sind die meisten Formeln in der Physik deutlich einfacher als das zuletzt gezeigte Beispiel!

Beachte stets die Grundregeln, und Du kommst Schritt für Schritt der gesuchten Gleichung näher.

Wenn Du sicherer wirst, kannst Du auch gleich zwei Schritte auf einmal durchführen.

Beispiel:

Du möchtest die Gleichung  s=\frac {1}{2}at^{2}  nach t umformen.

Dabei kannst Du die Schritte “Multiplizieren mit 2” und “dividieren durch a” zusammenfassen:

s=\frac {1}{2}at^{2}          \vert \cdot 2   \vert :a     bzw.     \vert \cdot \dfrac {2}{a}

Wenn Du dann beide Seiten vertauschst, erhältst Du

t^{2}=\dfrac {2s}{a}          \vert \sqrt {}

Anschließend ziehen wir die Wurzel und erhalten für t

t=\sqrt {\dfrac {2s}{a}}

Übungsaufgaben

Hier findest Du weitere Übungsaufgaben zum Umstellen von Formeln. Versuche zunächst, die Lösung wie in den Beispielen oben selbst zu finden, und vergleiche sie dann mit der vorgegebenen Lösung. Die Lösung erscheint, wenn Du auf “Lösung” oder auf das Symbol “∨“ klickst!

Aufgabe 1

Stelle die Gleichung     F=-D\cdot s     nach \boldsymbol {s} um!

Lösung

F=-Ds          \vert :{-D}   / Seiten vertauschen

s=-\dfrac {F}{D}

Aufgabe 2

Stelle die Gleichung     E_{kin}=\frac {1}{2}mv^{2}     nach \boldsymbol {v} um!

Lösung

E_{kin}=\frac {1}{2}mv^{2}          \vert\cdot 2

2E_{kin}=mv^{2}          \vert :m     / Seiten vertauschen

v^{2}=\dfrac {2E_{kin}}{m}          \vert\sqrt {}

v=\sqrt {\dfrac {2E_{kin}}{m}}

Aufgabe 3

Stelle die Gleichung     F_{z}=\dfrac {mv^{2}}{r}     nach \boldsymbol {r} um!

Lösung

F_{z}=\dfrac {mv^{2}}{r}         \vert\cdot r

F_{z}r=mv^{2}          \vert :F_{z}

r=\dfrac {mv^{2}}{F_{z}}

Aufgabe 4

Stelle die Gleichung     f=\dfrac {1}{2 \pi \sqrt {LC}}     nach \boldsymbol {L} um!

Lösung

f=\dfrac {1} {2 \pi \sqrt{LC}}         \vert\cdot \sqrt {LC}

f \cdot \sqrt {LC}=\dfrac {1}{2 \pi}          \vert :f        ⇒ Hinweis zum Dividieren eines Bruchs s. unten!

\sqrt {LC}=\dfrac {1}{2 \pi f}          \vert \; (\;)^{2}  (alles quadrieren)

LC=\dfrac {1}{(2 \pi f)^{2}}          \vert :C

L=\dfrac {1}{(2 \pi f)^{2}\cdot C}        oder (Klammer ausmultipliziert):        L=\dfrac {1}{4 \pi^{2} f^{2} C}

Aufgabe 5

Stelle die Gleichung     N(t)=N_{0} \cdot e^{-\lambda t}     nach \boldsymbol {t} um!

Lösung

In der gegebenen Gleichung steht die gesuchte Größe im Exponenten.

Zunächst wollen wir jedoch auf der rechten Seite den Faktor N_{0} loswerden. Dafür dividieren wir durch ihn:

N(t)=N_{0} \cdot e^{-\lambda t}          \vert \, :N_{0}

Um an den Exponenten zu gelangen, müssen wir die Umkehrfunktion zur Exponentialfunktion anwenden. Dies ist der natürliche Logarithmus ln.

\dfrac {N(t)}{N_{0}}=e^{-\lambda t}          \vert \, ln

Logarithmieren der gesamten Gleichung führt zu

ln \, \dfrac {N(t)}{N_{0}}=-\lambda t          \vert \, :(-\lambda)

t=\dfrac {ln \left( \dfrac {N(t)}{N_{0}} \right)} {-\lambda}

Das Minuszeichen ließe sich noch loswerden, indem man vom Bruch hinter dem Logarithmus den Kehrwert bildet, denn es gilt:

\dfrac {N_{0}}{N(t)}=e^{\lambda t}          (wenn man Zähler und Nenner vertauscht, kehrt sich das Vorzeichen im Exponenten um)

Damit ergibt sich für die Zeit t:

t=\dfrac {ln \left( \dfrac {N_{0}}{N(t)} \right)} {\lambda}

Vermeide Doppelbrüche!

In Aufgabe 4 mussten wir einen Bruch durch eine weitere Größe teilen:

f \cdot \sqrt {LC}=\dfrac {1}{2 \pi}          \vert :f

Dies kommt recht häufig vor. Man könnte nun natürlich die Größe f einfach unter einen neuen Bruchstrich schreiben:

\sqrt {LC}=\dfrac {\frac {1}{2 \pi}}{f}

Das wird jedoch schnell unübersichtlich und ist unnötig, denn Doppelbrüche lassen sich ganz einfach auflösen bzw. von vornherein vermeiden.

Schreiben wir den Bruch auf der rechten Seite ausnahmsweise einmal anders (mit “:”):

\dfrac {\frac {1}{2 \pi}}{f}=\dfrac {1}{2 \pi}:f

Wenn wir diesen Bruch durch f teilen, dann bedeutet das, wir müssen ihn mit dem Kehrwert – also mit \dfrac {1}{f} – multiplizieren:

\dfrac {1}{2 \pi}:f=\dfrac {1}{2 \pi}\cdot \dfrac {1}{f}

Wir können das zu einem Bruch zusammenfassen, indem wir jeweils die Zähler und Nenner multiplizieren:

\dfrac {1}{2 \pi}\cdot \dfrac {1}{f}=\dfrac {1\cdot 1}{2 \pi \cdot f}=\dfrac {1}{2 \pi f}

Letztendlich haben wir nichts anderes getan, als dass wir den Nenner mit der Größe, durch die der Bruch dividiert werden soll, multipliziert haben.

Die einfache Regel beim Dividieren eines Bruchs durch eine Größe lautet also:

Dividieren bei Brüchen:

Wenn ein Bruch durch eine Größe dividiert werden soll, dann multipliziere den Nenner mit dieser Größe!

Zur weiteren Übung zum Formeln umstellen kannst Du jede beliebige Gleichung immer wieder zu jeder Größe hin umformen. Je mehr Übung Du hast, umso leichter wird es Dir fallen, und umso weniger Fehler wirst Du machen!

Hat Dir diese Anleitung geholfen? Waren die Erklärungen verständlich?

Ansonsten wäre ich für ein Feedback dankbar! Schreibe einfach über das Kontaktformular, was Dir fehlt oder was Du nicht verstanden hast!

In diesem Video von studyfix wird das Formeln umstellen auch noch einmal an einfachen Beispielen erklärt.

>> Hier findest Du weitere Hilfe zum erfolgreichen Lösen von Physikaufgaben! <<

weitere Hilfsmittel