Überlagerung von Bewegungen – das Unabhängigkeitsprinzip
Ein Körper kann eine Bewegung ausführen, die sich aus mehreren Teilbewegungen zusammensetzt. So bewegt sich ein Schwimmer in einem Fluss zum einen aufgrund seiner Muskelkraft und zum anderen infolge der Strömung des Wassers.
Ein geworfener Ball bewegt sich aufgrund der ihm verliehenen Anfangsgeschwindigkeit, zugleich fällt er aufgrund der stets wirkenden Gravitation nach unten.
Für die Überlagerung von Teilbewegungen gilt das Unabhängigkeitsprinzip oder Superpositionsprinzip.
Statt von Überlagerung spricht man auch von Superposition und vom Superpositionsprinzip. Es gilt für Geschwindigkeiten, die klein gegenüber der Lichtgeschwindigkeit sind.
Führt ein Körper gleichzeitig zwei reibungsfreie Teilbewegungen aus, so überlagern sich diese Teilbewegungen unabhängig voneinander zu einer resultierenden Bewegung. Weg, Geschwindigkeit und Beschleunigungen addieren sich vektoriell
Viele Überlagerungen von Bewegungen lassen sich auf die Überlagerung zweier gleichförmiger Bewegungen oder einer gleichförmigen und einer gleichmäßig beschleunigten Bewegung zurückführen.
Überlagerung zweier gleichförmiger Bewegungen
Die Teilbewegungen können in gleicher, in entgegengesetzter (gegen den Strom schwimmen) oder in beliebigen anderen Richtungen zueinander erfolgen. Betrag und Richtung der Geschwindigkeiten der Teilbewegungen sind konstant.
Beispiel 1: Beide Bewegungen haben die gleiche Richtung
Bewegt man sich auf einem Rollsteig (z.B. auf dem Flughafen) in die gleiche Richtung wie der Rollsteig, so addieren sich die Geschwindigkeiten von Rollsteig und der Person. Beide Bewegungen sind unabhängig voneinander und überlagern sich zu einer resultierenden Bewegung.
Angenommen, die Person bewegt sich mit 
auf einem Rollsteig, dessen Geschwindigkeit 
beträgt, so ergibt sich als resultierende Geschwindigkeit
Die Person bewegt sich also mit einer resultierenden Geschwindigkeit von 7km/h.
Beispiel 2: Beide Bewegungen haben die entgegengesetzte Richtung
Betritt man einen solchen Rollsteig in die falsche Richtung und bewegt man sich in die Gegendichtung zum Rollband, so addieren sich wiederum die Geschwindigkeiten, wobei eine der Geschwindigkeiten negativ ist:
Die resultierende Geschwindigkeit entspricht also der Differenz der Beträge der Geschwindigkeiten.
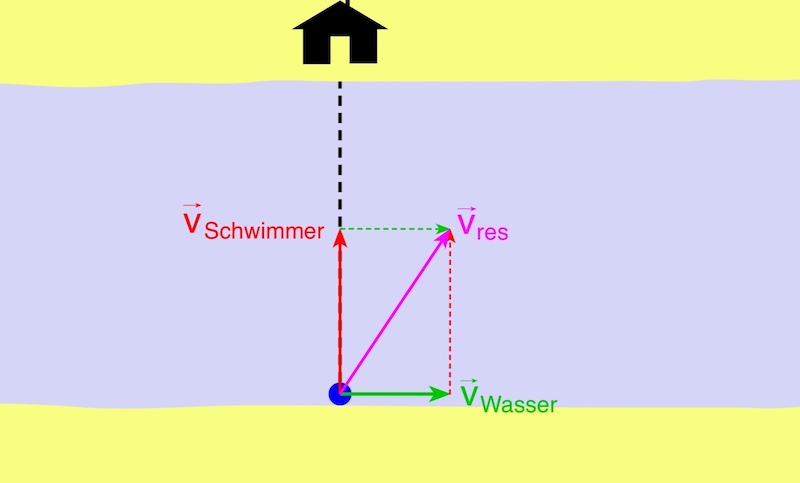
Beispiel 3: Beide Bewegungen stehen senkrecht zueinander
Überlagern sich zwei Teilbewegungen, die senkrecht zueinander stehen, so ergibt sich die resultierende Geschwindigkeit aus der vektoriellen Addition beider Geschwindigkeiten.
Beispiel:
Ein Schwimmer durchquert einen Fluss und schwimmt direkt auf ein Haus auf der gegenüberliegenden Seite des Flusses zu. Doch dabei überlagert sich die Schwimmgeschwindigkeit mit der Geschwindigkeit des strömenden Wassers – der Schwimmer bewegt sich deshalb schräg zum Ufer.
Angenommen der Schwimmer schwimmt mit einer Geschwindigkeit von 
, und das Wasser fließt senkrecht dazu mit 
, so gilt für die resultierende Geschwindigkeit
Wir dürfen nun allerdings nicht einfach die Beträge (Zahlenwerte) addieren oder subtrahieren, da die Bewegungen weder die gleiche noch die entgegengesetzte Richtung haben. Wir müssen sie vektoriell addieren:
Da beide Geschwindigkeiten senkrecht zueinander stehen, können die resultierende Geschwindigkeit auch berechnen. Dazu benötigen wir den Satz des Pythagoras:
Es gilt:
Damit ergibt sich:
Die resultierende Geschwindigkeit ist also deutlich kleiner als die Summe der Beträge der einzelnen Geschwindigkeiten.
Überlagerung einer gleichförmigen und einer beschleunigten Bewegung
Wenn sich eine gleichförmige mit einer gleichmäßig beschleunigten Bewegung überlagert, so ergibt sich keine konstante resultierende Geschwindigkeit, da sich die Geschwindigkeit einer der Teilbewegungen konstant ändert.
Das ist bei allen Arten von Würfen der Fall, denn dabei überlagern sich die gleichförmige Bewegung aufgrund der Anfangsgeschwindigkeit mit der gleichmäßig beschleunigten Bewegung des freien Falls.
Auf den nächsten Seiten erfährst Du alles über die verschiedenen Wurfbewegungen!