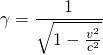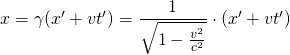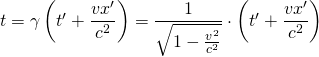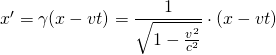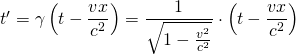Eine Konsequenz aus den beiden Postulaten lautet:
Es existiert kein Äther und kein absolutes Bezugssystem!
Nach den Galilei-Transformationen kann in der klassischen Mechanik nur eine unendlich große Geschwindigkeit in allen Bezugssystemen den gleichen Wert haben. Die Lichtgeschwindigkeit nimmt somit den Stellenwert einer solchen unendlich hohen Geschwindigkeit ein. Das bedeutet:
Kein Körper, keine Wirkung und kein Signal kann schneller sein als das Licht.
Die Konstanz der Lichtgeschwindigkeit hat weitreichende Konsequenzen, die unsere Vorstellung von Raum und Zeit grundlegend verändern. Zum Beispiel folgt daraus die Relativität des Begriffs der Gleichzeitigkeit sowie die Relativität der Zeitdauer von Vorgängen.
Die Umrechnung der Koordinaten von einem Inertialsystem in ein anderes ist mit Hilfe der Galilei-Transformation möglich, solange die Geschwindigkeiten vernachlässigbar gegenüber der Lichtgeschwindigkeit sind. Für größere Geschwindigkeiten müssen diese Gleichungen jedoch modifiziert werden.
Die Lorentz-Transformation
Die Gleichungen, die es ermöglichen, die räumlichen und zeitlichen Koordinaten unter Berücksichtigung der Postulate der speziellen Relativitätstheorie von einem Inertialsystem in ein anderes umzurechnen, werden als Lorentz-Transformation bezeichnet.
Sie wurden erstmals von H. A. Lorentz aufgestellt und unabhängig davon von Einstein auf Grundlage seiner Relativitätstheorie abgeleitet.
Zur Herleitung der Lorentz-Transformation gehen wir wieder davon aus, dass sich ein Inertialsystem 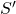 gegenüber einem System
gegenüber einem System 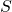 mit der Geschwindigkeit
mit der Geschwindigkeit  in positive x-Richtung bewegt:
in positive x-Richtung bewegt:
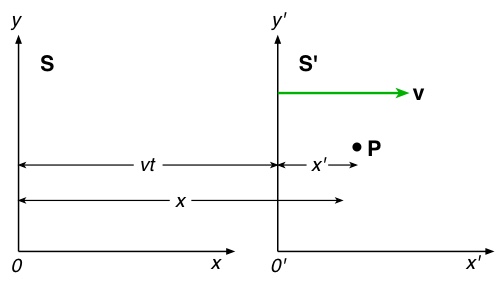
Wir nehmen an, dass die Gleichungen der Transformation die Form
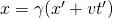 ,
, 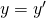 ,
,  (1)
(1)
haben.
Wir modifizieren also die Gleichung der Galilei-Transformation mit einem noch unbekannten Faktor 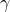 („gamma“, für Geschwindigkeiten v << c, also nicht relativistisch, gilt:
(„gamma“, für Geschwindigkeiten v << c, also nicht relativistisch, gilt: 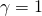 ). Die Gleichungen für
). Die Gleichungen für 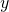 und
und  bleiben unverändert.
bleiben unverändert.
Die Gleichungen für die umgekehrte Transformation müssen dieselbe Form haben, wenn  durch –
durch – ersetzt wird.
ersetzt wird.
Es muss also ebenfalls gelten:
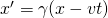 . (2)
. (2)
Verlässt nun ein Lichtimpuls zur Zeit 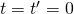 den gemeinsamen Ursprung von
den gemeinsamen Ursprung von 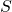 und
und 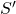 , so hat er zur Zeit
, so hat er zur Zeit 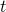 eine Entfernung von
eine Entfernung von 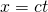 oder
oder 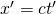 entlang der x-Achse zurückgelegt.
entlang der x-Achse zurückgelegt.
Aus den Gleichungen (1) und (2) ergibt sich so
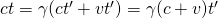 (3)
(3)
sowie
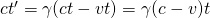 (4)
(4)
Setzt man 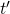 aus Gleichung (4) in Gleichung (3) ein, so ergibt sich
aus Gleichung (4) in Gleichung (3) ein, so ergibt sich
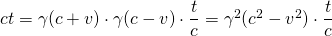
Dividieren durch 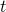 und Auflösen nach
und Auflösen nach 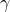 führt zu
führt zu
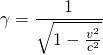
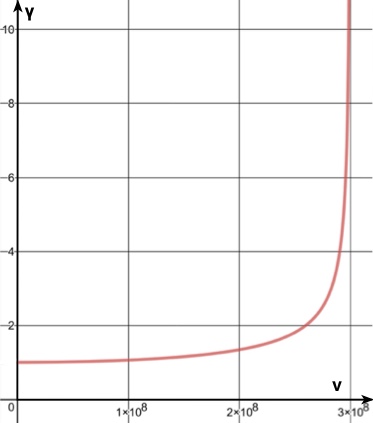
Mit dem nun bekannten Faktor 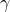 , der auch als Lorentz-Faktor bezeichnet wird, lässt sich die Beziehung zwischen
, der auch als Lorentz-Faktor bezeichnet wird, lässt sich die Beziehung zwischen 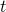 und
und 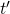 herleiten.
herleiten.
Dazu setzen wir Gleichung (1) [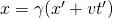 ] in Gleichung (2) [
] in Gleichung (2) [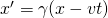 ] ein und erhalten:
] ein und erhalten:
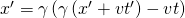
Löst man diese Gleichung nach 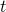 auf, so erhält man
auf, so erhält man
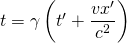
Es ergibt sich also, dass die Zeiten 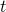 und
und 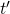 nicht identisch sind, sondern sich unterscheiden.
nicht identisch sind, sondern sich unterscheiden.
Insgesamt ergeben sich folgende Gleichungen für die Lorentz-Transformation: