Brechung von Licht

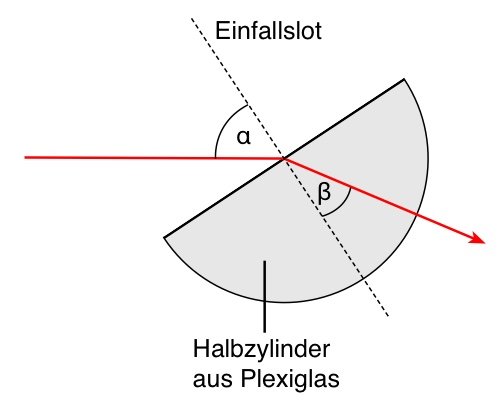
Lichtbrechung

Licht kann sich nicht nur in Luft oder im Vakuum (luftleerer Raum), sondern auch in anderen Medien, wie z.B. Wasser oder Glas, ausbreiten. Medien, in denen sich Licht ausbreiten kann, bezeichnet man als durchsichtig. Doch wenn Licht in ein anderes Medium eindringt, lässt sich ein besonderes Phänomen beobachten, das man als Brechung bzw. Lichtbrechung bezeichnet. Die Brechung von Licht soll mit Hilfe zweier Versuche demonstriert werden:

Versuch 1:

Eine Münze wird in eine leere Tasse gelegt. Nun schaut man von oben schräg auf die Tasse, so dass die Münze gerade hinter dem Tassenrand verschwunden ist, so dass man sie nicht sehen kann. Dann wird die Tasse mit Wasser gefüllt.

Beobachtung:

Nachdem die Tasse mit Wasser gefüllt wurde, kann man die Münze sehen, so als wäre sie angehoben worden:

Versuch 2:

Ein Lineal, ein Trinkhalm oder ein Stift wird schräg in ein mit Wasser gefülltes Gefäß (Becher, Tasse oder Glas) getaucht. Nun blickt man von oben auf die Wasseroberfläche. Beobachtung: Der Gegenstand erscheint abgeknickt, und zwar an der Stelle, an der er ins Wasser eintaucht (s. Foto rechts).

Wodurch entsteht dieser Eindruck?

Da wir wissen, dass die Münze in Versuch 1 nicht angehoben wurde, und das Lineal bzw. der Stift in Versuch 2 gerade verläuft, handelt es sich um ein optisches Phänomen. Wenn ein Gegenstand an einer anderen Stelle erscheint als er wirklich ist, dann liegt dies daran, dass das Licht einen anderen Weg nimmt als gewohnt.

Normalerweise breitet sich das Licht geradlinig aus. Doch an der Grenzfläche zwischen zwei Medien (hier: Wasser und Luft), wird das Licht abgeknickt. Dieses Phänomen bezeichnet man als Brechung von Licht. Dadurch, dass wir es gewohnt sind, dass sich Licht immer geradlinig ausbreitet, vermuten wir den Gegenstand an einem anderen Ort – so als käme das Licht von dort aus geradlinig in unser Auge:

Das Licht wird an der Grenzfläche zwischen Wasser und Luft gebrochen.

Die Münze erscheint dadurch an einem anderen Ort, als sie tatsächlich liegt.

Lässt man ein schmales Lichtbündel schräg in ein mit Wasser gefülltes Becken oder einen Quader aus Glas bzw. Plexiglas einfallen, so sieht man, dass das Licht an der Grenzfläche abknickt und die Richtung ändert. Man sagt, das Licht wird gebrochen (s.o.). Der Winkel gegenüber dem Einfallslot, mit dem es sich im Wasser oder Glas ausbreitet, wird Brechungswinkel β genannt. Dieser ist kleiner als der Einfallswinkel α. Man sagt, das Licht wird zum Lot hin gebrochen.

Tritt das Licht senkrecht auf die Grenzfläche (α = 0°), so tritt keine Brechung auf. Das Lichtbündel verläuft weiter in der ursprünglichen Richtung.

Übergang eines Lichtbündels beim Eintritt in Wasser oder Glas

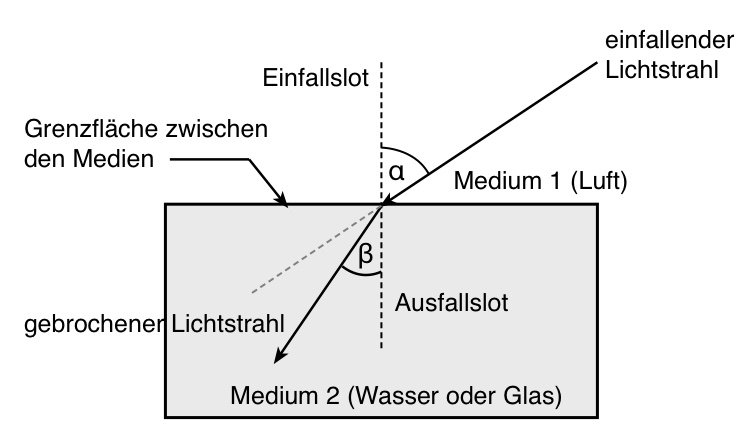Ein Lichtbündel wird beim Übergang von Luft in ein anderes optisches Medium zum Lot hin gebrochen.

Was bedeutet optisch dichter bzw. optisch dünner?

Luft und Glas bzw. Wasser, also verschiedene optische Medien, haben offensichtlich unterschiedliche optische Eigenschaften, obwohl sie alle lichtdurchlässig sind. Die Ursache für die Brechung ist, dass sich das Licht in verschiedenen optischen Medien unterschiedlich schnell ausbreitet.

Optische Medien werden als optisch dichter bzw. als optisch dünner im Vergleich zu anderen optischen Medien bezeichnet:

Das Medium, in dem der kleinere der beiden Winkel liegt, wird als optisch dichter bezeichnet.

(Die Lichtgeschwindigkeit in diesem Medium ist kleiner.)

Das Medium, in dem der größere Winkel liegt, wird als optisch dünner bezeichnet.

(Die Lichtgeschwindigkeit in diesem Medium ist größer.)

Aus den Versuchen ergibt sich also: Wasser und Glas sind optisch dichter als Luft.

Auch bei der Brechung gilt: Der Lichtweg ist umkehrbar

Die Umkehrbarkeit des Lichtweges gilt auch bei der Brechung.

Das bedeutet: Geht das Licht von einem optisch dichteren (Wasser oder Glas) in ein optisch dünneres Medium (Luft) über, so wird es vom Lot weg gebrochen. Der Brechungswinkel β wäre dann kleiner als der Einfallswinkel α.

Daraus ergibt sich folgender Zusammenhang:

Auf die Frage, welches Medium optisch dichter bzw. dünner ist, gilt natürlich anders herum:

Wird das Licht beim Übergang von Medium 1 in Medium 2 zum Lot hin gebrochen, so ist Medium 2 optisch dichter.

Wird das Licht beim Übergang von Medium 1 in Medium 2 vom Lot weg gebrochen, so ist Medium 2 optisch dünner.

Zusammenhang zwischen Einfalls- und Brechungswinkel

Wenn das Licht in ein anderes Medium übergeht, so wissen wir, dass der Brechungswinkel sich gegenüber dem Einfallswinkel ändert. Doch wie groß ist der Brechungswinkel, und wovon hängt er ab?

Um diese Frage zu klären, lässt man ein Lichtbündel unter verschiedenen Einfallswinkel in ein optisch dichteres Medium fallen, und misst jeweils den Einfallswinkel sowie den Brechungswinkel. Die gemessen Werte werden in eine Tabelle eingetragen.

Anschließend werden in einem Diagramm Einfalls- und Brechungswinkel gegeneinander aufgetragen.

Für diesen Versuch eignet sich besonders gut ein Halbzylinder aus Plexiglas. Man lässt das Licht auf der geraden Seite einfallen, so dass man den Einfallswinkel mit Hilfe einer Winkelscheibe einfach ablesen kann. Auf der runden Seite tritt das Licht ohne Brechung (also ohne Richtungsänderung) wieder hinaus, weil es auf diese Grenzfläche stets senkrecht trifft (s.o.). So lässt sich auch der Brechungswinkel einfach ablesen:

Es lässt sich ablesen:

Der Einfallswinkel (linke Seite) beträgt 30°, der Brechungswinkel (rechte Seite) ist kleiner und beträgt 20°.

In der folgenden Skizze sind jeweils Einfalls- und Brechungswinkel sowie das Einfallslot eingezeichnet:

Bei diesem Versuch stellt man fest, dass die Richtungsänderung des Lichtbündels umso stärker ist, je größer der Einfallswinkel ist, also je schräger das Licht auf die Oberfläche trifft. Die Messwerte für 8 verschiedene Einfallswinkel sind in der folgenden Tabelle dargestellt. Der Einfallswinkel kann natürlich nicht 90° oder größer sein, da dann kein Licht mehr auf die Grenzfläche treffen würde.

Einfallswinkel α	10°	20°	30°	40°	50°	60°	70°	80°
Brechungswinkel β	6,6°	13,2°	19,5°	25,4°	30,7°	35,3°	38,8°	41°

Stellt man den Brechungswinkel in Abhängigkeit vom Einfallswinkel in einem Diagramm dar, so ergibt sich folgender Verlauf:

Brechungswinkel β in Abhängigkeit vom Einfallswinkel α

Man erkennt, dass der Zusammenhang zwischen Brechungs- und Einfallswinkel nicht proportional ist. je größer der Einfallswinkel ist, umso stärker nimmt der Brechungswinkel zu.

Im Diagramm ist die Kurve bis zum (theoretisch maximal möglichen) Einfallswinkel von α = 90° verlängert. Man erkennt: Auch der Brechungswinkel β nähert sich einem Höchstwert, den er nicht überschreiten kann. Dieser maximal mögliche Brechungswinkel hängt von den optischen Medien ab. Man bezeichnet ihn als Grenzwinkel β_g. In diesem Beispiel (Übergang von Luft in Plexiglas) beträgt der Grenzwinkel β_g ca. 42°.

Mit Hilfe des Diagramms lässt sich für jeden beliebigen Einfallswinkel der zugehörige Brechungswinkel ablesen, auch für Winkel, die wir gar nicht gemessen haben.

Außerdem lässt sich das Diagramm auch umgekehrt verwenden:

Beim umgekehrten Lichtweg, also beim Übergang von Plexiglas (optisch dichter) nach Luft (optisch dünner), wäre der Brechungswinkel größer als der Einfallswinkel. Vertauscht man die Achsen, so lässt sich der Brechungswinkel auch für den umgekehrten Lichtweg ablesen.

Geht das Licht durch eine planparallele Platte aus einem optischen Medium hindurch, so wird es beim Eintritt zum Lot hin und beim Austritt vom Lot weg gebrochen.

Das folgende Bild zeigt ein Lichtbündel, welches auf der oberen Seite eines Plexiglaskörpers eintritt und unten wieder austritt. Das unten austretende Lichtbündel hat wieder die gleiche Richtung wie das oben eintretende Lichtbündel:

Außerdem erkennt man, dass ein Teil des Lichts jeweils an den Grenzflächen (beim Übergang zwischen Luft und Plexiglas) reflektiert wird.

Lichtbrechung am Prisma

Unter einem optischen Prisma versteht man einen Körper aus Glas oder einem anderen optischen Medium (Plexiglas etc.) mit einem Dreieck als Grundfläche.

Gegenüber der planparallelen Platte (s.o.) sind die Seiten eines Prismas nicht parallel. Das Licht im Prisma wird auch zweimal gebrochen – beim Eintritt und beim Austritt – jedoch jeweils in die gleiche Richtung und nicht wieder zurück.

Das folgende Bild zeigt die Brechung eines schmalen Lichtbündels (roter Laser) an einem Glasprisma:

Man sieht, dass das Licht zweimal in die gleiche Richtung gebrochen wird und so insgesamt stärker abgelenkt wird als an anderen Körpern.

In folgendem Bild, in dem ein etwas kleineres Prisma mit einem grünen Laser bestrahlt wird, sieht man zusätzlich noch die Reflektionen, die auftreten – sowohl an der Außenseite beim Eintritt in das Prisma als auch an der Innenseite, an der das Licht in das Prisma zurück reflektiert wird und unten austritt:

Totalreflexion von Licht

Möchte man mit Hilfe des Diagramms den Brechungswinkel für den umgekehrten Lichtweg (Übergang vom optisch dichteren ins optisch dünnere Medium) ermitteln, so wird man feststellen:

Für den Fall, dass der Einfallswinkel größer ist als der Grenzwinkel von ca. 42°, kann man gar keinen Brechungswinkel mehr ablesen.

Doch was passiert, wenn man ein Lichtbündel unter einem größeren Winkel auf die Grenzfläche Plexiglas → Luft treffen lässt? Wir wollen dies in einem Versuch herausfinden. Statt Plexiglas verwenden wir Wasser, aus dem das Licht einer Lampe von unten auf die Wasseroberfläche trifft.

Versuch:

Eine Lampe mit einer Blende mit mehreren Schlitzen erzeugt unter Wasser mehrere schmale Lichtbündel, die unter verschiedenen Winkeln von unten auf die Wasseroberfläche treffen:

Beobachtung:

• Die Lichtbündel, die unter einem kleinen Winkel auf die Wasseroberfläche treffen werden beim Übergang zur Luft vom Lot weg gebrochen. Ein Teil des Lichts wird an der Wasseroberfläche reflektiert.
• Die Lichtbündel, die in einem großen Winkel auf die Wasseroberfläche treffen, verlassen das Wasser nicht mehr, sondern werden an der Wasseroberfläche nur noch (“total”) reflektiert. Man spricht daher von Totalreflexion.

Das folgende Bild zeigt, wie das Licht eines Lasers innerhalb eines Plexiglasstabes immer wieder total reflektiert wird. An jeder Grenzfläche zwischen Plexiglas und Luft ist der Grenzwinkel zur Totalreflexion überschritten:

Dieses Phänomen wird in sogenannten Lichtleitern genutzt. Diese bestehen aus Glasfasern. Darin wird das Licht weitergeleitet und tritt erst am Ende wieder aus – auch wenn die Glasfasern gebogen werden.