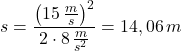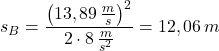Bremsweg und Anhalteweg
Beim Bremsen aufgrund einer Verkehrssituation (plötzlich auftretendes Hindernis etc.) ist jedoch nicht allein der Bremsweg dafür entscheidend, ob es zu einem Unfall kommt oder nicht, denn zunächst dauert es eine gewisse Zeit (Reaktionszeit), bis der Fahrer überhaupt auf ein Ereignis reagieren und damit den Bremsvorgang einleiten kann.
Bis dahin fährt das Auto mit unverminderter Geschwindigkeit weiter!
Den in dieser Zeit zurückgelegten Weg bezeichnet man als Reaktionsweg.
Der Anhalteweg setzt sich also aus dem Bremsweg und dem Reaktionsweg zusammen.
Die Reaktionszeit
Die Reaktionszeit eines Menschen hängt von vielen Faktoren ab, wie der Art des Ereignisses (akustisch, optisch etc.), der Aufmerksamkeit, der Art der Reaktion (hier: bremsen) etc.
Ist man darauf trainiert, auf ein bestimmtes Signal auf eine bestimmte Art und Weise zu reagieren, wie z.B. als Sprinter im Startblock bei einem 100 m-Lauf, kann die Reaktionszeit weniger als 0,15 Sekunden betragen.
Info:
Startet ein Sprinter früher als 0,10 Sekunden nach dem Startschuss, wird dies als Fehlstart interpretiert, da man davon ausgehen kann, dass es unmöglich ist, innerhalb einer deart kurzen Zeitspanne auf den Startschuss zu reagieren. Diese Grenze ist jedoch umstritten, da Studien auf mögliche Reaktionszeiten von unter 85 ms hindeuten.
Im Straßenverkehr kann man jedoch nicht ständig auf jedes Ereignis vorbereitet sein. Außerdem ist man häufig abgelenkt (z.B. durch Gespräche mit dem Beifahrer), so dass die Reaktionszeit beim Autofahren meist deutlich höher ist. Sie wird meist mit 0,5-0,8 Sekunden angenommen. Dazu kommt noch die Zeit, bis die Bremse nach Betätigung ihre maximale Bremswirkung entfaltet.
Man kann davon ausgehen, dass die Zeit zwischen Ereignis (plötzlich auftretendes Hindernis etc.) und Beginn des Bremsvorganges in den meisten Fällen bei etwa einer Sekunde liegt.
Während dieser Zeit fährt das Auto mit unverminderter Geschwindigkeit (also gleichförmig) weiter.
Den Weg, den das Auto in dieser Zeit zurücklegt, bezeichnet man als Reaktionsweg.
Berechnung des Anhalteweges
Wie bereits beschrieben setzt sich der Anhalteweg zusammen aus Reaktionsweg und dem eigentlichen Bremsweg:
Anhalteweg = Reaktionsweg + Bremsweg
oder kürzer in einer Formel:
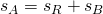
Beispielrechnung:
Wir nehmen an, dass ein Auto mit einer Geschwindigkeit von 54km/h unterwegs ist und die durchschnittliche Bremsbeschleunigung 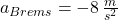 beträgt. Als Reaktionszeit nehmen wir eine Sekunde an.
beträgt. Als Reaktionszeit nehmen wir eine Sekunde an.
Reaktionsweg
Innerhalb der Reaktionszeit, also vor dem Bremsvorgang, fährt das Auto mit gleichbleibender Geschwindigkeit weiter. Es gelten also die Gesetze der gleichförmigen Bewegung.
Der Reaktionsweg lässt sich mit dem Weg-Zeit-Gesetz der gleichförmigen Bewegung berechnen:
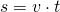
Hier ist  der Reaktionsweg
der Reaktionsweg 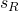 und t die Reaktionszeit
und t die Reaktionszeit 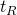 .
.
Reaktionsweg: 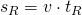
Wir setzen die o.g. Werte ein. Die Geschwindigkeit in m/s beträgt 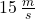 .
.
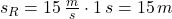
Ergebnis: Der Reaktionsweg beträgt 15 m.
Bremsweg
Beim Bremsweg gehen wir von einer gleichmäßig beschleunigten Bewegung mit negativer Beschleunigung aus.
Es gilt das Weg-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung:
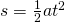
Da wir die Bremszeit nicht kennen, dafür aber die Geschwindigkeit bzw. die Geschwindigkeitsänderung, benötigen wir außerdem das
Geschwindigkeit-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung:
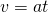
Damit lässt sich 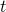 bzw.
bzw. 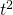 ersetzen:
ersetzen:
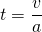 bzw.
bzw. 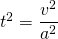
Eingesetzt in des Weg-Zeit-Gesetz ergibt sich:
Bremsweg: 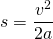
Nun setzen wir die Werte ein:
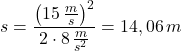
Ergebnis: Der Bremsweg beträgt 14,06 m.
Hinweis:
Da sowohl Geschwindigkeitsänderung als auch Beschleunigung negativ sind, kürzt sich das negative Vorzeichen weg. Letztendlich kann man es auch gleich weglassen, da ein negativer Bremsweg keinen Sinn macht.
Anhalteweg
Der Anhalteweg ergibt sich nun aus der Summe von Reaktionsweg und Bremsweg:
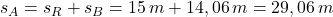
Ergebnis: Der Anhalteweg beträgt 29,06 m.
![]() und damit die Beschleunigung negativ. Entscheidend in vielen Situationen ist der Bremsweg eines Fahrzeuges.
und damit die Beschleunigung negativ. Entscheidend in vielen Situationen ist der Bremsweg eines Fahrzeuges.
![]()