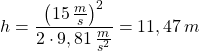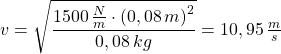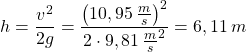Energie und Energieerhaltung - Energieformen und Energieumwandlungen

Energie – eine der wichtigsten Größen in der Physik

Arbeit und Energie sind grundlegende Größen zur Beschreibung physikalischer Vorgänge. Energie ist eine Erhaltungsgröße. Das bedeutet, sie kann weder erzeugt noch vernichtet werden.

Energie tritt in verschiedenen Formen auf, die ineinander umgewandelt werden können.

Arbeit und Energie

Um einen Körper zu beschleunigen, wir eine Kraft benötigt. Der Zusammenhang aus Kraft und Beschleunigung wird in der Grundgleichung der Mechanik beschrieben:

$F=m\cdot a$

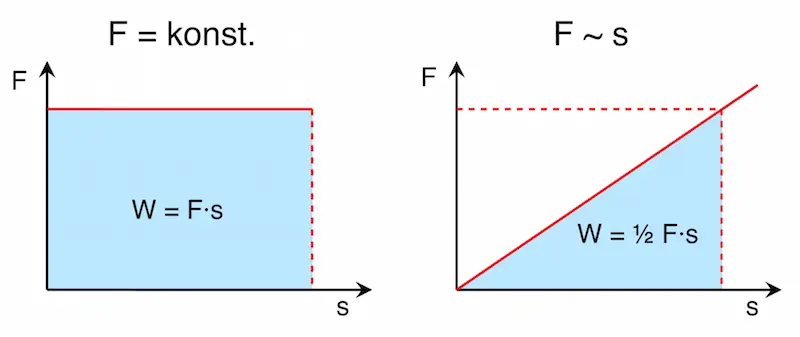
Die Kraft, die einen Körper um eine Weglänge s verschiebt, verrichtet die Arbeit

$W=F\cdot s$

Beispiel:

Ein Körper mit einer Masse von m = 5 kg wird um eine Höhe von h = 2 m angehoben.

Die dazu notwendige Hubarbeit beträgt

$W=F\cdot s$

wobei F die Gewichtskraft [ $F_{G}=mg$ ] ist und die Strecke s der Höhe h entspricht:

$W=F_{G}\cdot h=m\cdot g\cdot h$

Setzt man die o.g. Werte ein, erhält man für die verrichtete Hubarbeit

$W=5\, kg\cdot 9,81\, \frac {N}{kg}\cdot 2\, m=98,1\, Nm \left( J \right)$

Dadurch, dass an dem Körper Hubarbeit verrichtet wurde, steigt seine Energie. Die Energie, die ein Körper aufgrund seiner Lage (bzw. Höhe) besitzt, nennt man Lageenergie oder potentielle Energie.

Dabei gilt: Die zugeführte Lageenergie entspricht der aufgewendeten Hubarbeit.

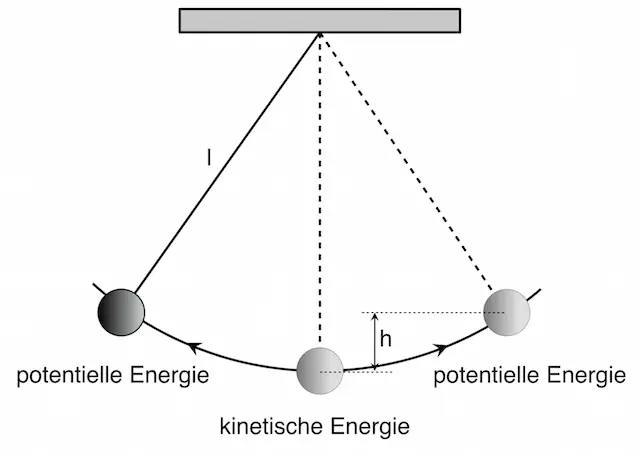
Wenn der Körper anschließend fallen gelassen wird, wird am Körper Beschleunigungsarbeit verrichtet. Dabei wird die Lageenergie in Bewegungsenergie (kinetische Energie) umgewandelt. Beim Aufprall auf den Boden wird der Körper verformt / erwärmt. Die kinetische Energie wird dabei in Wärmeenergie umgewandelt.

Definition und Eigenschaften der Energie

Durch Arbeit, die an einem Körper verrichtet wurde, wird die Energie des Körpers erhöht. Arbeit, die der Körper verrichtet, mindert seine Energie. Die Arbeit verursacht dabei eine Änderung des Zustands, in dem sich der Körper befindet (Verschiebung, Beschleunigung, Verformung, Erwärmung etc.).

Energie ist ein Maß dafür, wie viel Arbeit einem Körper zugeführt wurde bzw. von ihm verrichtet wurde.

Arbeit und Energie haben die gleiche Einheit, nämlich das Joule (J).

Es gilt: 1 J = 1 Nm

Mechanische Energieformen

Es gibt verschiedene Formen mechanischer Energie.

Wir wollen nun die wichtigsten mechanischen Energieformen definieren und anschließend Beispiele für Umwandlungen zwischen diesen Energieformen untersuchen.

1. Potentielle Energie (Lageenergie)

Wird ein Körper angehoben, so wird an ihm Hubarbeit verrichtet. Dadurch erhöht sich seine potentielle Energie (Lageenergie).

Potentielle Energie

Das Arbeitsvermögen, dass jeder Körper aufgrund seiner Lage (Höhe) besitzt, nennt man Lageenergie oder potentielle Energie E_pot.

Die potentielle Energie eines Körpers beträgt

$E_{pot}=m\, g\, h$

Dabei wird die Höhe von einem frei wählbaren Nullpunkt aus gemessen. In physikalischen Vorgängen sind letztendlich immer Energiedifferenzen entscheidend.

Das Arbeitsvermögen bzw. die Energie, die ein Körper nach dem Anheben besitzt, ist genauso groß wie die aufgewendete Hubarbeit. Man kann also sagen:

Lageenergie ist gespeicherte Hubarbeit.

Arbeit und Energie haben die gleiche Einheit, nämlich das Joule (J).

Es gilt: 1 J = 1 Nm

2. Kinetische Energie

Die durch Beschleunigungsarbeit zugeführt Energie der Bewegung bezeichnet man als Bewegungsenergie oder kinetische Energie E_kin. Je größer die Geschwindigkeit und je größer die Masse eines Körpers ist, umso größer ist seine kinetische Energie.

Formel zur Berechnung der kinetischen Energie

Wirkt eine konstante Kraft F auf einen Körper entlang einer Stecke s, so wird dieser gleichmäßig beschleunigt. Am Körper wird die Beschleunigungsarbeit $W=F\cdot s$ verrichtet.

Die kinetische Energie entspricht der verrichteten Arbeit, also gilt:

$E_{kin}=F\cdot s$

Die Kraft ergibt sich aus dem Produkt aus Masse und Beschleunigung [ $F=m\cdot a$ ]. Damit gilt:

$E_{kin}=m\cdot a\cdot s$

Für gleichmäßig beschleunigte Bewegungen gilt das Weg-Zeit Gesetz $s=\frac {1}{2}\cdot a \cdot t^{2}$ .

Damit gilt für die kinetische Energie

$E_{kin}=m\cdot a\cdot \left( \frac {1}{2}a\cdot t^{2}\right)$

Anders geschrieben:

$E_{kin}=\frac {1}{2}\cdot m \left( a\cdot t\right)^{2}$

Das Produkt aus Beschleunigung und Zeit entspricht der Geschwindigkeit: $a\cdot t=v$ .

Damit ergibt sich für die kinetische Energie

$E_{kin}=\frac {1}{2}mv^{2}$

Kinetische Energie (Bewegungsenergie)

Die durch Beschleunigungsarbeit zugeführte Energie, die ein Körper aufgrund seiner Geschwindigkeit besitzt, bezeichnet man als Bewegungsenergie oder kinetische Energie E_kin.

Die kinetische Energie eines Körpers beträgt

$E_{kin}=\frac {1}{2}mv^{2}$

Beispiel zur Berechnung der kinetischen Energie:

Ein Auto mit einer Masse von m = 950 kg bewegt sich mit einer Geschwindigkeit von v = 120 km/h.

Zur Berechnung muss die Geschwindigkeit zunächst in die Einheit m/s umgerechnet werden. Das ergibt: v = 33,33 m/s.

Damit erhält man für die kinetische Energie:

$E_{kin}=\frac {1}{2}\cdot 950\,kg\cdot \left(33,3\, \frac {m}{s}\right)^{2}=527.777,8\, J$

Energieumwandlungen und Energieerhaltung

Fällt ein Körper aus einer Höhe h herunter, so verringert sich seine potentielle Energie. Doch die Energie verschwindet nicht, sie wird in kinetische Energie umgewandelt.

Unmittelbar vor dem Auftreffen auf dem Boden (bei h = 0), ist die potentielle Energie vollständig in kinetische Energie umgewandelt worden.

Während des Fallens verringert sich also die potentielle Energie, die kinetische Energie steigt.

Die Summe beider Energieformen bleibt dabei konstant. Sie ergeben zusammen die Gesamtenergie des Systems.

Das gilt nicht nur in diesem Beispiel sondern für alle Prozesse. Dies ist ein grundlegendes Prinzip und lässt sich folgendermaßen formulieren:

Energieerhaltungssatz

Die Gesamtenergie eines abgeschlossenen Systems bleibt bei allen Vorgängen konstant.

Energie kann nur umgewandelt werden, geht aber nicht verloren.

Wenn man von “Energiegewinnung” oder “Energieverlust” spricht, ist dabei immer die Umwandlung in andere Energieformen gemeint.

Beispiel für Energieumwandlungen

In einem Kohlekraftwerk wird die chemische Energie aus der Kohle durch Verbrennung in Wärmeenergie umgewandelt. Dadurch wird Wasser verdampft, der Wasserdampf treibt Turbinen an. Dabei wird Wärmeenergie in mechanische Energie (kinetische Energie) umgewandelt. Die Turbinen sind an einen Generator gekoppelt, der die kinetische Energie durch Induktion in elektrische Energie umwandelt.

Energieumwandlung in Wärmekraftwerken:

Chemische Energie → Wärmeenergie → kinetische Energie → elektrische Energie

In Kraftwerken wird also keine Energie erzeugt, sondern nur umgewandelt.

Leider lässt sich nicht die gesamte chemische Energie in elektrische Energie umwandeln. Nach den Gesetzen der Thermodynamik ist es prinzipiell nicht möglich, eine Maschine zu bauen, die Wärmeenergie kontinuierlich vollständig in mechanische Energie umwandeln kann. Ein Teil der Energie wird immer als Wärme an die Umgebung abgegeben, geht also scheinbar “verloren“.

Bei der Umwandlung mechanischer Energieformen (z.B. potentielle Energie in kinetische Energie oder umgekehrt) wird (durch Reibung) meist nur ein sehr kleiner Teil der Energie in Wärme umgewandelt. Ist die Reibung vernachlässigbar, der “Energieverlust” also minimal, kann man praktisch von einer vollständigen Umwandlung zwischen mechanischen Energieformen ausgehen.

Was kann man mit dem Energieerhaltungssatz anfangen?

Mit Hilfe des Energieerhaltungssatzes lassen sich viele physikalische Probleme auf sehr einfache Art lösen.

Vernachlässigt man bei der Umwandlung zwischen mechanischen Energieformen die Reibung und damit den Anteil der in Wärme umgewandelten Energie, so lassen sich durch Gleichsetzen der beiden Energieformen alle beteiligten Größen einfach berechnen.

Dazu ein einfaches Beispiel:

Berechnung der Fallgeschwindigkeit einer Kugel mit dem Ansatz der Energieerhaltung

Wir haben bereits mit Hilfe der Bewegungsgesetze den Zusammenhang zwischen Fallgeschwindigkeit und Fallhöhe hergeleitet.

Für die Geschwindigkeit in Abhängigkeit von der Fallhöhe ergab sich: $v=\sqrt {2gh}$ .

Wir wollen diesen Zusammenhang nun mit dem energetischen Ansatz herleiten:

Während des freien Falls wird die potentielle Energie vollständig in kinetische Energie umgewandelt. Die Gesamtenergie bleibt konstant.

Man kann also beide Energien gleichsetzen:

$E_{kin}=E_{pot}$

Wir setzen nun die Größen ein und erhalten

$\frac {1}{2}mv^{2}=mgh$

Umstellen nach v liefert

$v^{2}=2gh$ bzw.

$v=\sqrt {2gh}$

Man erhält also die gleiche Formel wie mit Hilfe der Bewegungsgesetze. Die Herleitung ist jedoch ein wenig einfacher.

Auf ähnliche Art lassen sich viele weitere Probleme auf vergleichsweise einfache Weise lösen.

Weiteres Beispiel:

Wir wollen berechnen, welche Höhe eine mit einer Geschwindigkeit von v = 15m/s senkrecht nach oben geworfene Kugel erreicht.

Anstelle in der Formelsammlung nach den Formeln zum senkrechten Wurf zu suchen, wählen wir wieder den energetischen Ansatz und setzen kinetische und potentielle Energie gleich:

$E_{kin}=E_{pot}$

$\frac {1}{2}mv^{2}=mgh$

Wir lösen diese Gleichung nun nach der gesuchten Höhe h auf und erhalten:

$h=\dfrac {v^{2}}{2g}$

Auch diese Formel entspricht der bereits mit Hilfe der Bewegungsgesetze hergeleiteten Formel für die Steighöhe beim vertikalen Wurf.

Setzen wir die Werte ein, so erhalten wir für die Höhe

$h=\dfrac {\left(15\, \frac {m}{s}\right)^{2}}{2\cdot 9,81\, \frac {m}{s^{2}}}=11,47\, m$

3. Spannenergie

Eine weitere mechanische Energieform ist die Spannenergie.

Wird z.B. eine Schraubenfeder aus ihrer Ruhelage gestreckt oder gestaucht, so ist dazu ein Kraft nötig. Die Kraft bewirkt eine Verlängerung oder Verkürzung der Feder um eine Strecke $\Delta s$ , es muss also die Spannarbeit $W=F\cdot \Delta s$ verrichtet werden.

Diese Arbeit ist dann in der Feder als Spannenergie E_spann gespeichert.

Berechnung der Spannenergie

Die Spannenergie ergibt sich aus dem Produkt aus Kraft $F$ und Verlängerung der Feder $\Delta s$ :

$E_{spann}=F\cdot \Delta s$

Allerdings muss dabei beachtet werden, dass die Kraft während der Verlängerung nicht konstant ist, sondern mit zunehmender Verlängerung größer wird.

Für den Zusammenhang zwischen Kraft und Verlängerung einer Schraubenfeder gilt das Hooke’sche Gesetz: Kraft und Verlängerung sind zueinander proportional.

Hooke’sches Gesetz: $F\sim s$ bzw. $\dfrac {F}{s}=konst.$

Diese Konstante ist die sog. Federkonstante oder Federhärte D.

Damit lautet das Hooke’sche Gesetz $F=-Ds$

Das Minuszeichen drückt aus, dass es sich eine entgegen der Verlängerung gerichteten Kraft handelt. Man nennt sie deswegen auch Rückstellkraft.

Beispiel:

Wird eine Schraubenfeder mit einer Federkonstanten von $D=20\, \frac {N}{m}$ um 0,1 m verlängert, so ist dafür eine Kraft von $F=20\, \frac {N}{m}\cdot 0,1\, m=2\, N$ notwendig.

Um die verrichtete Spannarbeit und damit die der Feder zugeführten Spannenergie zu ermitteln, stellen wir die verrichtete Arbeit in einem Diagramm dar.

Trägt man die Kraft F und den Weg s, in dessen Richtung die Kraft wirkt, gegeneinander auf, so entspricht die verrichtete Arbeit der Fläche unter dem Diagramm.

Dies gilt sowohl für den Fall, dass die Kraft konstant ist (linkes Diagramm) als auch für den Fall, dass Kraft und Weg zueinander proportional sind wie im Beispiel der Schraubenfeder (rechtes Diagramm):

Die verrichtete Arbeit entspricht jeweils der Fläche unter dem Diagramm

Man erkennt:

Die verrichtete Arbeit und damit die zugeführte Energie beträgt im rechten Diagramm gerade die Hälfte des Produktes aus der Verlängerung s und der Kraft F, die diese bewirkt.

Für die Spannarbeit gilt also:

$W_{spann}=\frac {1}{2}F\cdot s$

Die benötigte Kraft F hängt von der Verlängerung s sowie der Federkonstanten D ab.

Für den Betrag der Kraft gilt: $F=D\cdot s$ (s.o.)

Ersetzt man die Kraft durch diesen Ausdruck, erhält man schließlich:

$W_{spann}=\frac {1}{2}Ds^{2}$

Spannenergie

Die durch Verlängerung oder Verkürzung einer Schraubenfeder zugeführte Energie bezeichnet man als Spannenergie E_spann.

Die Spannenergie einer gespannten Feder beträgt

$E_{spann}=\frac {1}{2}Ds^{2}$

Beispielaufgabe zur Spannenergie und Energieumwandlung

Eine Feder mit einer Federkonstanten von D = 15 N/cm wird um s = 8 cm gespannt.

a) Welche Spannenergie erhält sie dadurch?

b) Auf welche Geschwindigkeit kann sie eine Kugel mit einer Masse von m = 80 g beschleunigen, wenn die Spannenergie vollständig in kinetische Energie umgewandelt wird?

c) Wie hoch würde die Kugel bei senkrechtem Abschuss fliegen?

Lösungen:

a) Die Spannenergie beträgt $E_{spann}=\frac {1}{2}Ds^{2}$

Wichtig ist, dass wir Federkonstante und Verlängerung in den Basiseinheiten einsetzen, also D = 1500 N/m und s = 0,08 m:

$E_{spann}=\frac {1}{2}\cdot 1500\, \frac {N}{m}\cdot \left( 0,08\, m\right) ^{2}=4,8\, J$

Ergebnis: Die Spannenergie beträgt 4,8 J.

b) Die berechnete Spannenergie entspricht der kinetischen Energie. Wir können also beide Energien gleichsetzen:

$E_{kin}=E_{spann}$

Da die Spannenergie bereits berechnet wurde, können wir das Ergebnis verwenden:

$E_{kin}=\frac {1}{2}mv^{2}=4,8\, J$

Umstellen nach v liefert:

$v=\sqrt {\dfrac {2 \cdot E_{spann}}{m}}=\sqrt {\dfrac {2\cdot 4,8\, J}{0,08\, kg}}=10,95\, \frac {m}{s}$

Ergebnis: Die Kugel erreicht eine Geschwindigkeit von v = 10,95 m/s = 39,4 km/h.

Hinweis:

Die Berechnung der Geschwindigkeit ist auch ohne vorherige Berechnung der Spannenergie möglich.

Man wählt den gleichen Ansatz:

$E_{kin}=E_{spann}$

und setzt jeweils die Größen ein:

$\frac {1}{2}mv^{2}=\frac {1}{2}Ds^{2}$

Umstellen nach v liefert

$v=\sqrt {\dfrac {Ds^{2}}{m}}$

Alle Werte unter der Wurzel sind bekannt, und wir erhalten das gleiche Ergebnis:

$v=\sqrt {\dfrac {1500\, \frac {N}{m}\cdot \left(0,08\, m \right) ^{2}}{0,08\, kg}}=10,95\, \frac {m}{s}$

c) Nun wird die kinetische Energie in potentielle Energie umgewandelt. Es gilt also:

$E_{pot}=E_{kin}$

$mgh=\frac {1}{2}mv^{2}$

Umstellen nach h liefert (s.o.):

$h=\dfrac {v^{2}}{2g}=\dfrac {\left(10,95\, \frac {m}{s}\right)^{2}}{2\cdot 9,81\, \frac {m}{s}^{2}}=6,11\, m$

Ergebnis: Die Kugel erreicht ein Höhe von h = 6,11 m.

Hinweis:

Auch die Höhe hätten wir ohne Berechnung der kinetischen Energie oder der Spannenergie berechnen können, denn alle Energien sind gleich groß:

$E_{pot}=E_{kin}=E_{spann}$

Wir können also potentielle Energie und Spannenergie gleichsetzen und erhalten:

$mgh=\frac {1}{2}Ds^{2}$

Umstellen nach h liefert:

$h=\dfrac {Ds^{2}}{2mg}$

Setzt man die Werte ein, so erhält man das gleiche Ergebnis wie zuvor:

$h=\dfrac {1500\, \frac {N}{m}\cdot \left( 0,08\, m\right)^{2}}{2\cdot 0,08\, kg\cdot 9,81\, \frac {m}{s^{2}}}=6,11\, m$

Energieumwandlung beim Fadenpendel

Nun wollen wir uns noch die Energieumwandlungen bei einem Fadenpendel anschauen:

Fadenpendel Eneegieumwandlung

Das Fadenpendel wird ausgelenkt, indem man den Pendelkörper aus seiner Ruhelage (tiefster Punkt in der Mitte) auslenkt und dabei um eine bestimmte Höhe h anhebt.

Es wird potentielle Energie zugeführt.

Lässt man den Pendelkörper los, so wird er entlang eines Kreisbogens in Richtung Ruhelage beschleunigt.

Die potentielle Energie wird in kinetische Energie umgewandelt.

Aufgrund seiner Trägheit bewegt sich der Pendelkörper über die Ruhelage hinaus zur anderen Seite. Ist die Reibung vernachlässigbar, so erreicht er wieder die gleiche Höhe wie bei der Auslenkung.

Die kinetische Energie wird wieder in potentielle Energie umgewandelt.

Dieser Prozess wiederholt sich so lange, bis das Pendel schließlich aufgrund von Reibung zur Ruhe kommt. Ohne Reibung würde dieser Prozess sich unendlich lange wiederholen.

Vernachlässigung der Reibung

Für eine einzelne Periode (eine Pendelbewegung) kann man die Reibung (und damit den “Energieverlust”) jedoch vernachlässigen.

Dann gilt:

Die Gesamtenergie, die sich aus der Summe der potentiellen und der kinetischen Energie ergibt, ist zu allen Zeiten konstant.

Mit Hilfe des energetischen Ansatzes lässt sich die Geschwindigkeit in der Ruhelage für eine bestimmte Auslenkung berechnen:

Beispiel:

Ein Pendel mit einer Länge von l = 1,50m wird um die Höhe h = 30 cm ausgelenkt und dann losgelassen.

Ansatz: Nach dem Loslassen wird bis zur Ruhelage die gesamte potentielle Energie in kinetische Energie umgewandelt.

Die kinetische Energie in der Ruhelage ist also gleich der potentiellen Energie im Umkehrpunkt. Damit gilt:

$E_{kin}=E_{pot}$

Für die Geschwindigkeit in der Ruhelage ergibt sich so

$v=\sqrt {2gh}=\sqrt {2\cdot 9,81\,\frac {m}{s^{2}}\cdot 0,3\,m}=2,42\,\frac {m}{s}$

Wir können also den gleichen Ansatz verwenden wie bei der Umwandlung von potentieller in kinetische Energie beim freien Fall (s.o.) und erhalten die gleiche Formel für die Geschwindigkeit!

Das bedeutet:

Es spielt überhaupt keine Rolle, auf welchem Weg ein Körper eine bestimmte Höhendifferenz überwindet. Die erreichte Geschwindigkeit hängt einzig und allen von der Höhendifferenz und damit von der Änderung der potentiellen Energie ab (solange die Reibung vernachlässigbar ist).

Wir erkennen:

1. Auch diese Aufgabe lässt sich einfach lösen, indem wir die Energien gleichsetzen.

2. Die Geschwindigkeit hängt nur von der Höhe ab und nicht davon, auf welchem Weg der Körper die Höhendifferenz zurückgelegt hat.

Die Geschwindigkeit ist die gleiche, als wenn der Körper aus der gleichen Höhe (hier: 30 cm) fallengelassen worden wäre.

Allerdings ist die Bewegungsrichtung eine andere – während sich ein Körper im freien Fall in Richtung der Schwerkraft nach unten bewegt, bewegt sich der Pendelkörper im tiefsten Punkt nach links oder rechts, also senkrecht zur Gewichtskraft.

Übungsaufgaben:

Cornelsen Oberstufe Physik Band 1 (1. Auflage 1998)

S. 54 A1

S. 56 A5

S. 57 A10

weiter mit Impuls und Impulserhaltung

zurück