* Die Quotienten in der rechten Spalte wurden jeweils für die einzelnen Abschnitte von 20cm berechnet. Dafür werden jeweils die Differenzen zwischen den Messwerten der jeweiligen Zeile und der darüberliegende Zeile gebildet.
Beispielrechnung für die dritte Zeile:
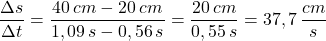
Die Berechnung der Quotienten für alle Abschnitte zeigt, dass diese mehr oder weniger konstant sind, was bedeutet, dass die Geschwindigkeit für alle Teilstrecken annähernd konstant ist. Die Abweichungen sind mit hoher Wahrscheinlichkeit auf Messfehler zurückzuführen.
Messfehler
Bei allen Messungen treten Fehler auf. Die Messung der Zeiten für die verschiedenen Teilstrecken ist recht ungenau, denn es entstehen Messfehler durch zu frühes oder zu spätes Betätigen der Stoppuhr beim Starten und Stoppen aufgrund der Reaktionszeit etc.
Die Genauigkeit der Messungen wird auf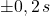 
geschätzt.
Bei Berücksichtigung dieser Messungenauigkeit lässt sich nicht eindeutig sagen, ob der Wagen immer gleich schnell war oder nicht. Eine bessere Beurteilung liefert eine grafische Auswertung der Messwerte.
Grafische Auswertung
Die Messwerte für die Strecke s und die Zeit t werden nun in einem Koordinatensystem gegeneinander aufgetragen.
Dafür muss zunächst eine Entscheidung über die Zuordnung der gemessenen Größen und den Koordinatenachsen getroffen werden.
Ändert sich eine Größe zeitlich, so ist es üblich, die Zeit auf der waagerechten Achse (Abszissenachse) und die andere Messgröße (in diesem Fall die Strecke) auf der senkrechten Achse (Ordinatenachse) aufzutragen.
Zurückgelegte Strecke s in Abhängigkeit von der Zeit t
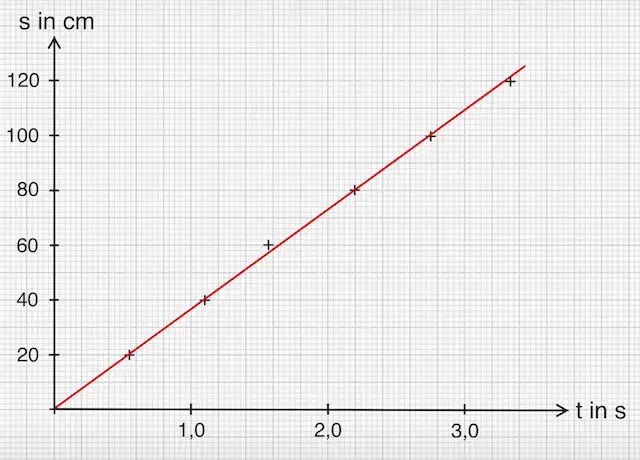
Ergebnis:
Alle Messpunkte liegen annähernd auf einer Geraden. Es ergibt sich also ein linearer Verlauf – Abweichungen werden als Messfehler (s.o.) interpretiert. Man zeichnet daher eine Ausgleichsgerade, die den Verlauf möglichst genau beschreibt.
Was bedeutet dieses Ergebnis?
Trägt man zwei Größen gegeneinander auf, und es ergibt sich dabei eine Gerade durch den Nullpunkt (Ursprungsgerade), so gilt: Die beiden Größten sind zueinander proportional.
In diesem Beispiel gilt also: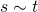 
(Strecke und Zeit sind zueinander proportional)
Außerdem gilt: Sind zwei Größen zueinander proportional, so ist ihr Quotient konstant.
Damit gilt also: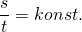 
Die Geschwindigkeit
Der Quotient aus zurückgelegtem Weg Δs und der dazu benötigten Zeit Δt ist definiert als Geschwindigkeit v:
Es gilt: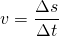 
Dieser Quotient – und damit die Geschwindigkeit – entspricht auch der Steigung im s-t-Diagramm:
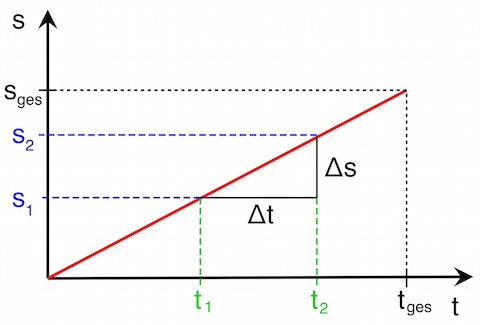
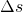sowie 
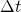sind bestimmte Abschnitte der Bewegung. Das griechische Symbol “
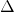” (“Delta”) steht für “Differenz”, und zwar für die Differenz zwischen zwei bestimmten Orten bzw. Zeiten, aus denen sich die jeweiligen Intervalle ergeben:
Hier gilt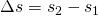 
und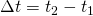 
(s. Skizze)
Ist die Steigung konstant, so macht es keinen Unterschied, wie groß die gewählten Intervalle sind – das Ergebnis ist das gleiche.
Allgemein gilt:
Die Steigung im Weg-Zeit-Diagramm entspricht der Geschwindigkeit v.
Da die Steigung und damit die Geschwindigkeit in diesem Beispiel konstant ist, handelt es sich um eine gleichförmige Bewegung. Bei einer gleichförmigen Bewegung werden in gleichen Zeitabschnitten gleich lange Strecken zurückgelegt.
Bei gleichförmigen Bewegungen ist es völlig egal, wo oder wie groß das Steigungsdreieck eingezeichnet wird, also wie groß die Intervalle 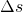und 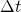gewählt werden. Die Geschwindigkeit ließe sich auch aus Gesamtstrecke 
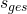und Gesamtzeit 
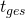berechnen.
Für gleichförmige Bewegungen gilt also ebenso
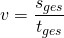oder ganz allgemein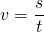 
Momentangeschwindigkeit und Durchschnittsgeschwindigkeit
Ist die Geschwindigkeit nicht über den gesamten betrachteten Zeitraum konstant, so unterscheidet man zwischen Momentan– und Durchschnittsgeschwindigkeit.
Das folgernde s-t-Diagramm zeigt eine ungleichförmige Bewegung – die Steigung und damit die Geschwindigkeit ist nicht konstant.
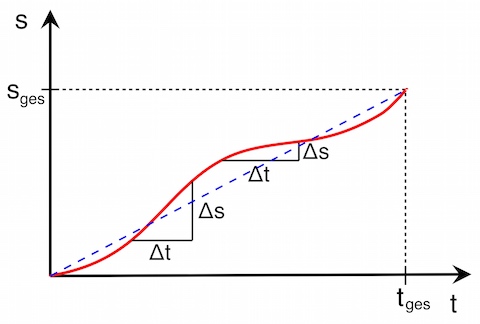
Diese Bewegung ist nicht gleichförmig
Möchte man die Geschwindigkeit ermitteln, so macht es nun einen Unterschied, welcher Abschnitt der Bewegung betrachtet wird.
Berechnet man nun die Geschwindigkeit mit der einfachen Formel 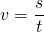, und setzt dabei Gesamtstrecke 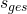und Gesamtzeit 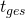ein, so erhält man nur die Durchschnittsgeschwindigkeit für den gesamten Zeitraum.
Die gestrichelte Gerade zeigt den Verlauf für eine gleichförmige Bewegung mit der gleichen Durchschnittsgeschwindigkeit. Doch wie man sieht, unterscheidet sich die Geschwindigkeit der ungleichförmigen Bewegung praktisch zu jedem Zeitpunkt deutlich von der gleichförmigen Bewegung.
Um die Geschwindigkeit genauer zu erfassen, müsste man diese für verschiedene Abschnitte ermitteln. Man erkennt an den beiden Steigungsdreiecken, dass sich jeweils verschiedene Geschwindigkeiten ergeben. Diese entsprechen jeweils der Durchschnittsgeschwindigkeit für die jeweiligen Abschnitte.
Unter Momentangeschwindigkeit versteht man die Geschwindigkeit zu einem bestimmten Zeitpunkt.
Die Momentangeschwindigkeit ändert sich bei einer ungleichförmigen Bewegung ständig. Diese ließe sich aus dem Diagramm nur annähernd ermitteln, indem der gewählte Zeitabschnitt und damit das Steigungsdreieck möglichst klein gehalten wird.
Info: Zur Berechnung der Steigung in einem Punkt kann man sich der Differentialrechnung bedienen – vorausgesetzt man kennt die Funktion, die den Verlauf im s-t-Diagramm beschreibt. Doch damit beschäftigen wir uns zu einem späteren Zeitpunkt.
Da sich die Geschwindigkeit bei gleichförmigen Bewegungen nicht ändert, entspricht die Momentangeschwindigkeit der Durchschnittsgeschwindigkeit.
Merke:
Bei gleichförmigen Bewegungen ist die Momentangeschwindigkeit gleich der Durchschnittsgeschwindigkeit.
Für gleichförmige Bewegungen gilt: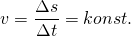 
Für nicht gleichförmige Bewegungen gilt: 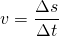ist nicht konstant!
Bei gleichförmigen Bewegungen gilt daher auch die vereinfachte Form
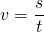(s.o.).
Diese Gleichung lässt sich nach s umstellen. So lässt sich für eine bekannte Geschwindigkeit v die zurückgelegte Strecke s für eine bestimmte Zeit t berechnen.
Für die Strecke gilt damit: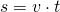 
Dieser Zusammenhang wird als Weg-Zeit-Gesetz für gleichförmige Bewegungen bezeichnet.
in 
*
