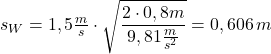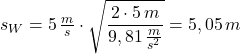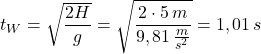Waagerechter oder horizontaler Wurf

Wird ein Körper horizontal abgeworfen, spricht man von einem waagerechten oder horizontalen Wurf.

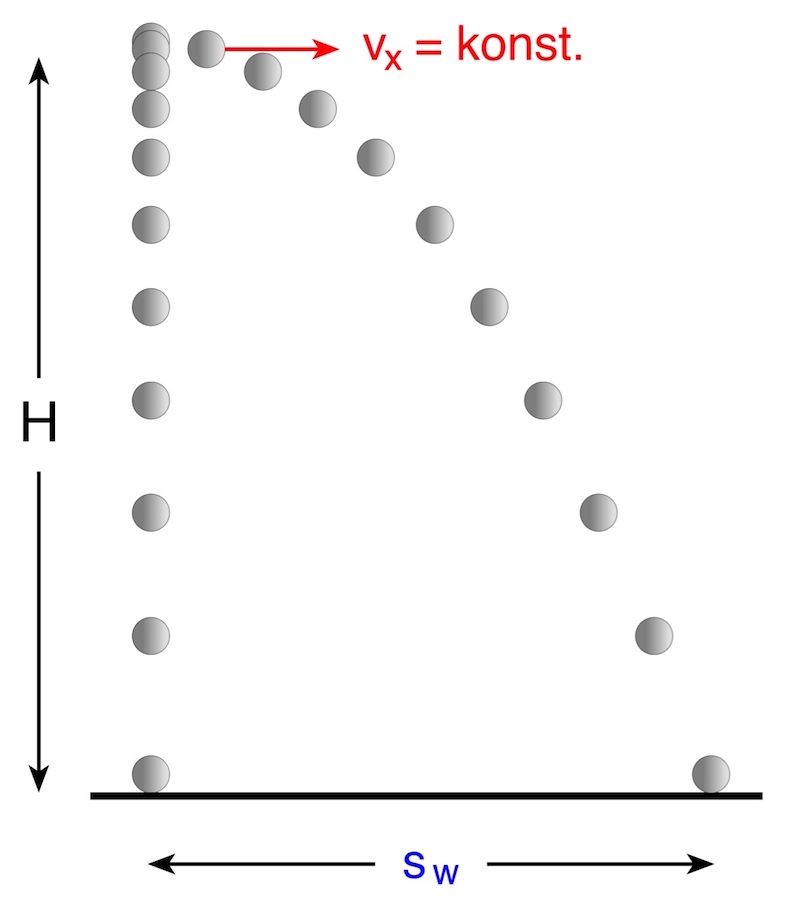
Beim horizontalen Wurf überlagert sich die gleichförmige Bewegung in horizontale (x-) Richtung mit der gleichmäßig beschleunigten Bewegung in vertikale (y-) Richtung. Es gibt also eine Anfangsgeschwindigkeit in x-Richtung v_{x}.

Für die Bewegung in y-Richtung gelten die Gesetze des freien Falls – genau wie für einen Körper, der ohne Bewegung in x-Richtung fallengelassen wird. Aus diesem Grund trifft eine horizontal geworfene Kugel zeitgleich mit einer aus der gleichen Höhe frei fallenden Kugel auf den Boden.

Das scheint zunächst widersprüchlich – schließlich legt die geworfene Kugel einen deutlich längeren Weg zurück.

Um dies genauer zu untersuchen, werden zwei gleichartige Kugeln in einer Vorrichtung so befestigt, dass eine Kugel durch ein gespannte Feder horizontal abgeworfen und die andere zeitgleich fallen gelassen wird.

Ergebnis:

Beide Kugeln treffen gleichzeitig auf den Boden.

Erklärung:

Nach dem Unabhängigkeitsprinzip überlagern sich beide Teilbewegungen ungestört, und wir können wir die beiden Teilbewegungen in x- und y-Richtung unabhängig voneinander betrachten. Die Fallbewegung in y-Richtung und damit die Fallzeit ist daher völlig unabhängig von der (gleichförmigen) Bewegung in x-Richtung.

Da in y-Richtung auf beide Kugeln die (gleiche) Schwerkraft wirkt, erfahren beide Kugeln die gleiche Beschleunigung in y-Richtung, nämlich die Erdbeschleunigung g, und kommen daher gleichzeitig auf dem Boden an.

Horizontaler Wurf - Freier Fall

Beide Kugeln legen in y-Richtung in der gleichen Zeit den gleichen Weg zurück. Zusätzlich legt die geworfene Kugel einen Weg in x-Richtung zurück. Der gesamte zurückgelegte Weg entspricht der Wurfweite s_{W}.

Die Bahn der geworfenen Kugel gleicht einer Parabelbahn. Dies lässt sich auch mit Hilfe eines Wasserstrahls, der horizontal einen Schlauch verlässt, zeigen – der Wasserstrahl beschreibt eine Parabelbahn.

Bahngleichung für den horizontalen Wurf

Dass es sich tatsächlich um eine Parabelbahn handelt, lässt sich mit Hilfe der Bewegungsgesetze zur gleichförmigen und gleichmäßig beschleunigten Bewegung zeigen.

Dazu betrachten wir die beiden Teilbewegungen unabhängig voneinander und stellen die entsprechenden Bewegungsgleichungen auf:

Für die Bahn in x-Richtung gilt:     s_{x}=v_{x}\cdot t        (1)

Für die Bahn in y-Richtung gilt:     s_{y}=-\frac {1}{2}g\cdot t^{2}        (2)

(Das negative Vorzeichen resultiert daraus, dass die sog. Wurfparabel nach unten offen ist.)

Unter einer Bahngleichung versteht man die Funktionsgleichung, also eine Gleichung in der Form y(x) = … Mit einer solchen Gleichung lässt sich für jede x-Position die entsprechende y-Position berechnen.

Die Bahngleichung einer Parabel hat die Form y(x)=a\cdot x^{2}, wobei a ein konstanter Faktor ist, der die Parabel streckt oder staucht. Ist a=1, so lautet die Funktionsgleichung y(x)=x^{2}. Es handelt sich dann um eine Normalparabel.

Um aus den o.g. Bewegungsgesetzen die Bahngleichung zu erhalten, muss die Zeit eliminiert werden.

Aus Gleichung (1) ergibt sich für die Zeit  t=\dfrac {s_{x}}{v_{x}}

Setzt man diesen Ausdruck für die Zeit in Gleichung (2) ein, so erhält man

y=-\dfrac {1}{2}g \cdot \left( \dfrac {s_{x}}{v_{x}} \right)^{2}

und damit

y=-\dfrac {1}{2}\dfrac {g}{v_{x}^{2}}\cdot s_{x}^{2}

Es handelt sich also tatsächlich um eine Parabelgleichung, da s_{x} quadratisch auf der rechten Seite steht.

Bahngleichung des horizontalen Wurfs

Ein horizontal (waagerecht) geworfener Körper beschreibt eine Parabelbahn.

Die Bahngleichung lautet:

y=-\dfrac {1}{2}\dfrac {g}{v_{x}^{2}}\cdot s_{x}^{2}

Dabei ist v_{x} die Anfangsgeschwindigkeit in horizontale (x-) Richtung.

Wurfweite beim horizontalen Wurf

Wir wollen nun eine Formel für die Wurfweite herleiten.

Die Wurfweite muss von der Anfangsgeschwindigkeit v_{x} sowie von der Abwurfhöhe H abhängen.

Ansatz:

Der Körper bewegt sich für die gesamte Wurfdauer, die gleich der Fallzeit beim freien Fall ist, gleichförmig in x-Richtung.

In dieser Zeit t legt der Körper den Weg  s_{x}=v_{x}\cdot t  zurück.

Die Fallzeit und damit die Wurfdauer hängt nur von der Abwurfhöhe H ab. Dabei gilt:

H=\dfrac {1}{2}gt^{2}

umgestellt nach t ergibt sich für die Wurfdauer

t_{W}=\sqrt {\dfrac {2H}{g}}        und damit die gleiche Formel wie für den freien Fall.

Der Weg in x-Richtung, der während dieser Zeit zurückgelegt wird, ist die gesuchte Wurfweite s_{W}.

Es gilt:        s_{x}=v_{x}\cdot t        und damit        s_{W}=v_{x}\cdot t_{W}

Wir setzen darin die Wurfdauer (s.o.) ein und erhalten für die Wurfweite

s_{W}=v_{x}\cdot \sqrt {\dfrac {2H}{g}}

Wurfweite und Wurfdauer beim horizontalen Wurf

Die Wurfweite s_{W} hängt von der Anfangsgeschwindigkeit in x-Richtung v_{x}

sowie von der Abwurfhöhe H ab:

s_{W}=v_{x}\cdot \sqrt {\dfrac {2H}{g}}

Die Wurfdauer t_{W} entspricht der Fallzeit des freien Falls:

t_{W}=\sqrt {\dfrac {2H}{g}}

Beispielaufgaben

Beispiel 1:

Eine Kugel rollt mit einer Geschwindigkeit von 1,5 m/s über eine Tischkante. Der Tisch hat eine Höhe von 0,8 m. In welcher Entfernung von der Tischkante trifft die Kugel auf den Boden?

Lösung:

Für die Wurfweite gilt:        s_{W}=v_{x}\cdot \sqrt {\dfrac {2H}{g}}

Einsetzen der Werte ergibt:

s_{W}=1,5 \frac {m}{s}\cdot \sqrt {\dfrac {2\cdot 0,8m}{9,81 \frac {m}{s^{2}}}}=0,606\, m

Antwort:

Die Kugel trifft 60,6cm hinter der Tischkante auf den Boden.

Info:

Auch die Bewegung bei Sprüngen entspricht der von Würfen. Es gelten die gleichen Gesetzmäßigkeiten.

Bei den meisten Aufgaben geht man von Körpern aus, bei denen die Ausdehnung des Körpers keine Rolle spielt – man betrachtet sie für die Berechnungen als punktförmig. Das ist bei Kugeln etc. problemlos möglich.

Bei größeren Körpern, wie bei Personen, Fahrzeugen etc. kann man die Ausdehnung der Körper jedoch nicht vernachlässigen. Mit den Bewegungsgesetzen sowie den Gesetzmäßigkeiten für Wurfbewegungen lässt sich nur die Bahn des Körperschwerpunktes berechnen. Zu beachten ist dabei, dass sich Teile des Körpers (z.B. die Füße) vor oder hinter der berechneten Bahn des Körperschwerpunktes befinden.

Beim Hochsprung ist es so möglich, größere Höhen zu überspringen als die maximale Höhe des Körperschwerpunktes.

Beispiel 2:

Wie weit vor der Kante des Sprungturms landet eine Person, die mit einer Anlaufgeschwindigkeit von 18km/h horizontal vom 5m-Turm abspringt?

Wie lange dauert es, bis er ins Wasser trifft?

Lösung:

Wir können hier nur die Bahn des Körperschwerpunktes (s.o.) berechnen.

Wir müssen zunächst die Anfangsgeschwindigkeit in die Einheit m/s umrechnen und benutzen anschließend wieder die Formel für die Wurfweite.

Es gilt:        v_{x}=18\, \frac {km}{h}=5\, \frac {m}{s}

Für die Wurfweite ergibt sich so        s_{W}=5\, \frac {m}{s}\cdot \sqrt {\dfrac {2\cdot 5\, m}{9,81\, \frac {m}{s^{2}}}}=5,05\, m

Die gesuchte Dauer entspricht der Fallzeit des freien Falls aus der gleichen Höhe:

t_{W}=\sqrt {\dfrac {2H}{g}}=\sqrt {\dfrac {2\cdot 5\, m}{9,81\, \frac {m}{s^{2}}}}=1,01\, s

Antwort:

Die Person landet nach einer Sekunde etwa 5 m vor der Kante im Wasser.

(Eine genauere Angabe macht keinen Sinn, da die Berechnung nur für den Körperschwerpunkt exakt gilt.)

weiter mit Schiefer Wurf
zurück