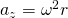Messen der Zentripetalkraft
Zur Messung der Zentripetalkraft auf einen rotierenden Körper, dient folgender Versuchsaufbau:
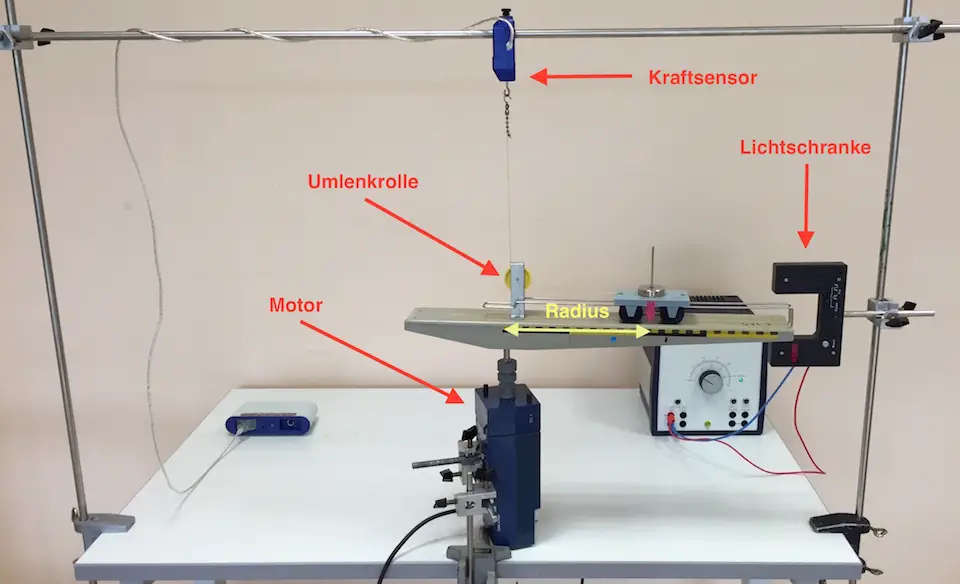
Eine Schiene, auf der sich ein Wagen befindet, wird mit Hilfe eines Motors in Rotation versetzt. Der Wagen ist über eine Umlenkrolle mit einem Kraftmesser verbunden, so dass die notwendige Zentripetalkraft gemessen werden kann.
Durch Veränderung der Höhe des Kraftsensors kann der Radius (= Abstand des Schwerpunkts des Wagens zum Kreismittelpunkt, s. Abbildung) variiert werden. Der Radius kann mit Hilfe des Zeigers und der Skala an der Schiene abgelesen werden.
Um die Masse des Wagens zu verändern, kann dieser mit zusätzlichen Gewichten bestückt werden.
Die Umlaufdauer wird mit Hilfe einer Lichtschranke bestimmt: Für jedem Umlauf wird die benötigte Zeit direkt an der Lichtschranke angezeigt – aus mehreren Messwerten kann so ein Mittelwert gebildet werden.
Messreihen
Um die Abhängigkeit der Zentripetalkraft von den o.g. Größen zu ermitteln, wird jeweils eine dieser Größen variiert, die anderen müssen konstant gehalten werden.
Es werden drei Messreihen durchgeführt:
1. Bestimmung der Zentripetalkraft in Abhängigkeit vom Radius r
Die Zentripetalkraft wird bei konstanter Drehfrequenz f bzw. Umlaufdauer T und konstanter Masse m für verschiedene Radien r bestimmt:
m = 150g = 0,15kg
T = 0,8s f = 1,25Hz
| r in cm |
10 |
13 |
16 |
19 |
25 |
| Fz in N |
0,9 |
1,25 |
1,5 |
1,8 |
2,3 |
2. Bestimmung der Zentripetalkraft in Abhängigkeit von der Drehfrequenz f
Die Zentripetalkraft wird bei konstanter Masse m und konstantem Radius r für verschiedene Drehfrequenzen f bestimmt:
m = 150g = 0,15kg
r = 25cm = 0,25m
| f in Hz |
0,63 |
1,04 |
1,25 |
1,56 |
1,85 |
| Fz in N |
0,6 |
1,6 |
2,3 |
3,6 |
5,1 |
3. Bestimmung der Zentripetalkraft in Abhängigkeit von der Masse m
Die Zentripetalkraft wird bei konstanter Drehfrequenz f und konstantem Radius r für verschiedene Massen m bestimmt:
r = 20cm = 0,2m
T = 1s f = 1Hz
| m in kg |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
| Fz in N |
0,8 |
1,2 |
1,6 |
2,0 |
2,4 |
Versuchsergebnisse und Auswertung
Aus den Messungen ergeben sich folgende Zusammenhänge:
1. Die Zentripetalkraft ist proportional zum Radius
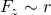
2. Die Zentripetalkraft ist proportional zum Quadrat der Drehfrequenz
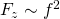
Da die Winkelgeschwindigkeit ω proportional zur Frequenz f ist (es gilt: 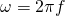 ), muss die Zentripetalkraft auch proportional zum Quadrat der Winkelgeschwindigkeit sein.
), muss die Zentripetalkraft auch proportional zum Quadrat der Winkelgeschwindigkeit sein.
Die Zentripetalkraft ist proportional zum Quadrat der Winkelgeschwindigkeit:
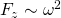
3. Die Zentripetalkraft ist proportional zur Masse
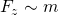
Zusammenfassung der Proportionalitäten
Aus den Zusammenhängen 1., 2. und 3. folgt:
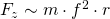 bzw.
bzw. 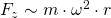
Der Quotient aus beiden Seiten ist damit konstant:
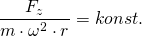 bzw.
bzw. 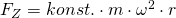
Setzt man die Einheiten aller Größen ein, so erkennt man:
Alle Einheiten lassen sich wegkürzen. Die Konstante hat also keine Einheit.
Ermittelt man den Zahlenwert der Konstanten aus den Messreihen, so ergibt sich annähernd der Wert 1. Man kann sie also einfach weglassen und erhält damit die gesuchte Formel:
Formel zur Berechnung der Zentripetalkraft:
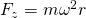
Um die Zentripetalkraft in Abhängigkeit von der Bahngeschwindigkeit berechnen zu können,
verwenden wir die Zusammenhänge 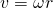 bzw.
bzw. 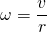 und
und 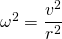
Eingesetzt in die Formel für die Zentripetalkraft (s.o.) ergibt sich damit eine weitere Formel:
Formel zur Berechnung der Zentripetalkraft:
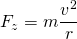
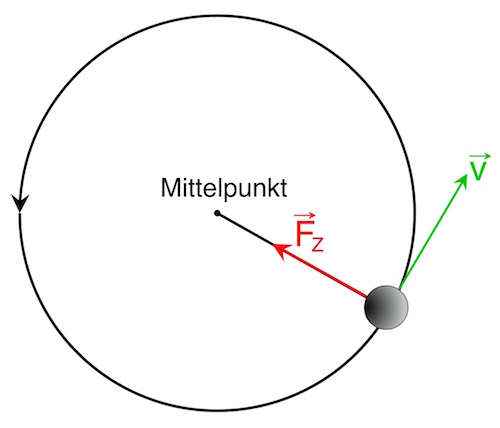
Für die Zentripetalbeschleunigung az gilt:
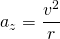 bzw.
bzw.