Newtonsche Bewegungsgesetze - Grundgleichung der Mechanik

Kraft und Beschleunigung

Nachdem wir innerhalb der Kinematik verschiedene Arten von Bewegungen untersucht haben, sollen wir uns nun mit der Ursache von Bewegungen bzw. von Bewegungsänderungen befassen:

Die Ursache für eine Bewegungsänderung (= Beschleunigung) ist immer eine Kraft.

Die Eigenschaft aller Körper, ohne Krafteinwirkung ihren Bewegungszustand beizubehalten, bezeichnet man als Trägheit.

Die Fundamente der klassischen Mechanik beruhen auf den von Isaac Newton 1687 formulierten Bewegungsgesetzen, die auch als Newton’sche Axiome bekannt sind (ein Axiom ist so etwas wie eine grundlegende Aussage).

1. Newtonsches Axiom (Trägheitsgesetz)

Ein Körper verharrt im Zustand der Ruhe oder der gleichförmigen geradlinigen Bewegung, solange er nicht durch einwirkende Kräfte zu einer Änderung des Bewegungszustandes gezwungen wird.

Die Alltagserfahrung kann zu falschen Vorstellungen führen

Nach dem Trägheitsgesetz müsste sich ein Körper in Bewegung mit unverminderter Geschwindigkeit immer weiter bewegen, so lange keine Kraft auf ihn wirkt, die ihn abbremst. Dies widerspricht scheinbar unserer Alltagserfahrung, denn um mit gleichbleibender Geschwindigkeit z.B. mit dem Auto oder mit dem Fahrrad weiterzufahren, müssen wir Gas geben oder weiter treten. Ohne eigenen Antrieb kommt jeder Körper auf der Erde irgendwann zum Stillstand.

Es tritt praktisch immer Reibung auf

Der Grund dafür ist jedoch nicht, dass keine Kraft wirkt, sondern vielmehr, dass praktisch immer eine weitere Kraft wirkt, nämlich die Reibungskraft. Diese sorgt in den meisten Fällen dafür, dass jeder Körper abgebremst wird.

Damit sich ein Körper gleichförmig weiterbewegt, muss die Reibungskraft überwunden werden, wozu letztendlich eine Antriebskraft benötigt wird.

Gibt es keine Reibung oder ist diese vernachlässigbar (Beispiele: Ein Wagen gleitet auf einer Luftkissenbahn oder eine Raumschiff schwebt im Weltall), wird für die Bewegung dagegen kein Antrieb benötigt.

Dass es Alltag praktisch immer Reibung gibt, führt häufig zu falschen Vorstellungen über den Zusammenhang zwischen Kraft und Bewegung, nämlich dass es ohne Kraft keine Bewegung gäbe und dass die Ursache für eine Bewegung eine Kraft sei.

Die Vorstellung, dass ein Körper eine Kraft besäße, die dem Körper mitgegeben wurde und mit der Zeit langsam aufgebraucht wird, gab es bereits im Mittelalter (→ Impetustheorie).

Diese Vorstellung ist jedoch falsch!

Es können nur durch Wechselwirkungen Kräfte auf einen Körper wirken. Ein Körper “besitzt” jedoch keine Kraft, sondern je nach Bewegungszustand nur Energie und Impuls.

Richtig ist:

Ein Körper, der in Bewegung ist, bleibt in (gleichförmiger) Bewegung, solange keine Kraft auf ihn wirkt.

Ein Körper, der in Ruhe ist, bleibt in Ruhe, solange keine Kraft auf ihn wirkt.

Eine Kraft kann eine Bewegungsänderung, also eine Beschleunigung bewirken.

Jeder Körper ist träge

Dass jeder Körper bestrebt ist, seinen Bewegungszustand beizubehalten, merkt man z.B., wenn man versucht, ein Auto anzuschieben, einen schweren Gegenstand aufzuhalten oder wenn man eine Tischdecke schnell vom Tisch zieht – die Gegenstände auf dem Tisch bewegen sich nicht mit der Decke mit sondern bleiben stehen, da sie träge sind.

Die Trägheit und damit die Kraft, die erforderlich ist, um einen Körper zu beschleunigen, hängt von seiner Masse ab – je größer die Masse eines Körpers ist, umso größer ist seine Trägheit.

Dabei gilt:

Ist die Beschleunigung konstant, so sind Kraft und Masse zueinander proportional:

$F\sim m$

Außerdem gilt:

Je größer die Kraft ist, die auf einen Körper wirkt, umso größer ist die Beschleunigung des Körpers. Bei konstanter Masse sind Kraft und Beschleunigung zueinander proportional:

$F\sim a$

Zusammen ergibt sich eine Proportionalität zwischen der Kraft und dem Produkt aus Masse und Beschleunigung:

$F\sim m\cdot a$

Der Proportionalitätsfaktor ist in diesem Fall “1”, so dass wir schreiben können: $F=m\cdot a$ . Das ist kein Zufall, sondern ist in der Festlegung der Einheit für die Kraft begründet:

Die Einheit der Kraft

Die Einheit der Kraft heißt “Newton“. Die Definition lautet:

1 Newton (N) ist die Kraft, die benötigt wird, um einen Körper der Masse 1kg aus der Ruhe in einer Sekunde auf die Geschwindigkeit 1m/s zu beschleunigen.

Das ist gleichbedeutend mit der Formulierung:

1 Newton (N) ist die Kraft, die benötigt wird, um einen Körper der Masse 1kg die Beschleunigung 1m/s² zu erteilen.

Die Aussage über die Proportionalität zwischen Kraft und dem Produkt aus Masse und Beschleunigung wird als zweites Newtonsches Axiom bezeichnet. (Ursprünglich wurde dabei jedoch die Kraft als Impulsänderung pro Zeit definiert in der Form $F\sim \dot v$ ).

2. Newtonsches Axiom (→ Grundgleichung der Mechanik)

Die Änderung der Bewegung (= Beschleunigung) ist zur einwirkenden Kraft proportional und hat die gleiche Richtung wie die einwirkende Kraft.

Hinweis: Der Proportionalitätsfaktor ist die Masse – bei konstanter Beschleunigung sind Kraft und Masse zueinander proportional.

Daraus ergibt sich die

Grundgleichung der Mechanik:

$\boldsymbol {F=ma}$

Die Gleichung $F=ma$ wird als Grundgleichung der Mechanik bezeichnet, da sie die Grundlage für viele Bewegungsgesetze in der Mechanik ist. Du solltest sie daher nie wieder vergessen!

Aus der Grundgleichung der Mechanik sowie aus der Definition der Kraft ergibt sich auch der Zusammenhang zwischen der Einheit Newton und den Basiseinheiten:

$1\,N=1\,\dfrac {kgm}{s^{2}}$

Die Einheit 1Newton lässt sich auf diese Weise also auch mit Basiseinheiten ausdrücken.

Aus dem zweiten Newtonschen Axiom ergibt sich die Tatsache, dass eine Beschleunigung immer eine Kraft als Ursache hat, und dass die Beschleunigung die gleiche Richtung hat wie die einwirkende Kraft.

Sowohl Kraft als auch Beschleunigung sind vektorielle Größen.

Die vektorielle Schreibweise der Grundgleichung der Mechanik lautet:

$\boldsymbol {\overrightarrow {F}=m\overrightarrow {a}}$

Beispiele und Anwendungen

Mit der Grundgleichung der Mechanik lässt sich für alle Körper bekannter Masse die Kraft berechnen, die für eine bestimmte Beschleunigung erforderlich ist:

Um einen Körper mit einer Masse von m = 60 kg um a = 1 m/s² zu beschleunigen, benötigt man eine Kraft von

$F=60\,kg\cdot 1\,\frac {m}{s^{2}}=60\,\frac {kgm}{s^{2}}=60\,N$ .

Genauso lässt sich die Beschleunigung berechnen, die eine bestimmte Kraft auf eine bekannte Masse bewirkt:

Wirkt auf einen Körper mit der Masse m = 60kg eine Kraft von 100N, so beträgt die Beschleunigung des Körpers

$a=\dfrac {F}{m}=\dfrac {100\,N}{60\,kg}=1,67\,\frac {m}{s^{2}}$

Hinweis:

Die erforderliche Kraft ist größer bzw. die Beschleunigung kleiner, wenn die Reibung nicht vernachlässigt werden kann.

Welche Kraft muss auf einen Körper wirken, damit er mit 9,81 m/s² beschleunigt wird?

Die genannte Beschleunigung ist die Fallbeschleunigung, also die Beschleunigung, mit der jeder frei fallende Körper (auf der Erde) beschleunigt wird.

Setzen wir diese Beschleunigung in die Grundgleichung der Mechanik ein, so erhalten wir:

$F=m\cdot 9,81\,\dfrac {m}{s^{2}}$ bzw. $F=m\cdot g$

Wir erhalten so die Gewichtskraft $F_{G}$ des Körpers – denn dies ist ja die Kraft, die jeden Körper beim freien Fall beschleunigt.

Die Gewichtskraft eines Körpers beträgt

$F_{G}=m\cdot g$

Diese Formel kennst Du bereits aus der Mittelstufe – da wurde die Fallbeschleunigung allerdings als Ortsfaktor bezeichnet.

Auf einen Körper der doppelten Masse wirkt also die die doppelte Gewichtskraft. Die Beschleunigung bleibt konstant.

Aus diesem Zusammenhang ergibt sich unmittelbar die Erkenntnis, dass alle Körper gleich schnell fallen!

Die Beschleunigung, die alle frei fallenden Körper erfahren, heißt Fallbeschleunigung g.

Die Fallbeschleunigung ist ortsabhängig und beträgt auf der Erde (bzw. in Erdnähe) $g=9,81\,\frac {m}{s^{2}}$ .

Diese Beschleunigung wird daher auch als Erdbeschleunigung bezeichnet.

Somit ist auch die Gewichtskraft eines Körpers ortsabhängig, während die Masse orstunabhängig ist.

Die Gewichtskraft und damit die Fallbeschleunigung g, die ein Körper erfährt, hängt von der Masse des Himmelskörpers ab.

Da der Mond eine deutlich kleinere Masse hat als die Erde, ist die Gravitation und damit die Fallbeschleunigung auf dem Mond deutlich kleiner als auf der Erde. Sie beträgt etwa $g_{Mond}=1,62\,\frac {m}{s^{2}}$ .

Info: Das Gravitationsgesetz

Newton stellte im jahre 1687 ein Gesetz auf, mit dem sich die Gravitationskraft zwischen zwei Körpern der Massen $m_{1}$ und $m_{2}$ , die sich im Abstand $r$ voneinander befinden, berechnen lässt.

Das Gravitationsgesetz lautet: $F=G\cdot \dfrac {m_{1}\cdot m_{2}}{r^{2}}$

Dabei ist $r$ der Abstand der Massenmittelpunkte und $G$ die Gravitationskonstante.

Die Gravitationskonstante hat den Wert $G=6,67\cdot 10^{-11}\,\dfrac {Nm^{2}}{kg^{2}}$ .

Aus dem Gravitationsgesetz folgt: Verdoppelt man den Abstand $r$ der beiden Massen, so verringert sich die Anziehungskraft zwischen den Massen um den Faktor 4.

Setzt man in das Gravitationsgesetz für $m_{1}$ die Erdmasse $m_{E}=5,997\cdot 10^{24}\,kg$ und für den Radius den Erdradius (Abstand zum Erdmittelpunkt) $r_{E}=6378\,km$ ein, so ergibt sich für eine Masse $m_{2}=1\,kg$ eine Gravitationskraft von $F=9,81\,N$ , also die die Gewichtskraft der Masse $m_{2}$ in Erdnähe.

In einer Höhe von 6378 km über der Erdoberfläche, also im Abstand $2r_{E}=12 756\,km$ vom Erdmittelpunkt, erfährt ein Körper nur noch 1/4 seiner Gewichtskraft auf dem Erdboden, da der Abstand vom Erdmittelpunkt doppelt so groß ist.

Auch auf der Erde ist die Fallbeschleunigung aufgrund schwankender Gravitation nicht überall gleich groß. U.a. wegen der Abflachung an den Polen ist die Fallbeschleunigung an den Polen größer als am Äquator.

Erdbeschleunigung an verschiedenen Orten auf der Erde:

Panama:

Mitteleuropa:

Hammerfest:

$g=9,78\,\frac {m}{s^{2}}$

$g=9,80665\,\frac {m}{s^{2}}$

$g=9,826\,\frac {m}{s^{2}}$

Das Wechselwirkungsprinzip

Die Gewichtskraft von $F_{G}=mg$ wirkt auf jeden Körper auf der Erde zu jeder Zeit.

Dass die Gewichtskraft außer beim freien Fall jedoch nicht dazu führt, dass alle Körper gleichermaßen beschleunigt werden, liegt daran, dass eine oder mehrere weitere Kräfte wirken.

Steht oder liegt ein Körper auf dem Boden oder auf einem Tisch, so gibt es jeweils eine weitere Kraft, die genauso groß ist wie die Gewichtskraft aber dieser entgegengerichtet ist. Diese Kraft wird vom Boden, vom Tisch etc. aufgebracht und führt dazu dass die Summe der auf den Körper wirkenden Körper 0 ist, wodurch es keine Änderung des Bewegungszustandes gibt.

Diese Kraft kann als Reaktionskraft bezeichnet werden – der Boden oder Tisch reagiert auf die Gewichtskraft des Körpers mit einer gleich großen entgegengerichteten Kraft. Könnte z.B. ein Tisch die entsprechende Reaktionskraft nicht aufbringen, so würde dieser zusammenbrechen.

Es ist nicht möglich, dass ein Körper eine Kraft auf einen zweiten Körper ausübt, ohne dass dieser nicht gleichermaßen eine Kraft auf den ersten Körper ausübt.

Dieser Zusammenhang wird auch als drittes Newtonsches Axiom, Wechselwirkungsprinzip oder auch als Gesetz von actio und reactio bezeichnet.

3. Newtonsches Axiom (Wechselwirkungsprinzip)

Kräfte treten immer paarweise auf. Übt der Körper A eine Kraft auf Körper B aus (actio), so übt Körper B eine gleich große aber entgegengerichtete Kraft auf Körper A aus (reactio).

Es gilt:

$\overrightarrow {F}_{A\rightarrow B}=-\overrightarrow {F}_{B\rightarrow A}$

Wer zieht wen an?

Das Wechselwirkungsprinzip gilt für alle Arten von Kräften.

Auf die Frage, ob wir von der Erde angezogen werden oder die Erde von uns, lautet die Antwort:

Wir ziehen die Erde mit der gleichen Kraft an, mit der wir von der Erde angezogen werden. Es handelt sich um eine wechselseitige Anziehung.

Dass wir in Richtung Erde fallen und nicht umgekehrt, liegt nur an der wesentlich größeren Masse der Erde und ihrer damit verbundenen Trägheit.

Das gleiche gilt auch für magnetische Anziehungs- oder Abstoßungskräfte. Genauso wie ein Magnet ein Stück Eisen anzieht, zieht das Stück Eisen den Magneten an – und zwar mit der gleichen Kraft!

Große Beschleunigungen erfordern große Kräfte

Soll ein Körper möglichst schnell beschleunigt werden (z.B. beim Anfahren eines Autos), so müssen entsprechend große Kräfte erzeugt werden.

Beim Anfahren eines Autos üben die Reifen eine Kraft auf die Straße aus. Die entsprechende Reaktionskraft der Straße auf die Reifen beschleunigt das Auto. Diese Kraft kann jedoch nicht größer sein als die Reibungskraft zwischen Reifen und Straße.

Das gleiche gilt auch beim Bremsen.

Da die Reibungskraft im Normalfall nicht größer sein kann als die Normalkraft (diese entspricht auf nicht geneigter Fahrbahn der Gewichtskraft), kann die Beschleunigung beim Anfahren und Bremsen nicht größer sein als die Fallbeschleunigung g.

Mit der Beschleunigung a = g ergibt sich im Idealfall eine Beschleunigung von 0 auf 100 km/h in 2,83 s sowie ein minimaler Bremsweg aus 100 km/h von 39,33 m.

Dass diese Werte z.T. im Realfall sogar übertroffen werden, liegt daran, dass neben der Reibungskraft weitere Effekte eine Rolle spielen können, die die Reaktionskraft vergrößern können.

Verletzungsgefahr beim Unfall

Bei Unfällen werden Fahrzeuge innerhalb kürzester Zeit aus hohen Geschwindigkeit bis zum Stillstand abgebremst. Das ist nur durch sehr große Kräfte möglich, die sowohl auf das Fahrzeug als auch auf die Insassen wirken.

Je größer die Geschwindigkeitsänderung pro Zeit (also je größer die Bremsbeschleunigung), umso größere Kräfte treten auf. Die Bremsbeschleunigung und damit die auf den Fahrer wirkende Kraft hängt von der Geschwindigkeit sowie vom Bremsweg ab. Dabei gilt: Je kleiner der Bremsweg und je höher die Geschwindigkeit, umso höher die Kräfte.

Fährt ein Auto gegen einen feststehenden Gegenstand, so ist der Bremsweg gerade so groß wie das Auto verformt werden kann. Dieser Bereich wird auch “Knautschzone” genannt.

Bei einem Unfall ist es daher nicht wünschenswert, dass das Auto so wenig wie möglich beschädigt wird, weil die auftretenden Kräfte dann noch größer wären. Vielmehr ist man bemüht, einen möglichst großen Bereich verformen zu lassen, wodurch die Unfallfolgen auf die Insassen reduziert werden sollen.

Berechnung der auf die Insassen eines Autos wirkenden Kräfte bei einem Unfall:

Angenommen ein Auto fährt mit 40 km/h frontal gegen ein Hindernis. Die Knautschzone betrage 80 cm.

Berechnung der Beschleunigung:

Aus den Bewegungsgesetzen ergibt sich für die Beschleunigung

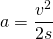$a=\dfrac {v^{2}}{2s}$ wobei s der Beschleunigungsweg ist, also hier die Knautschzone

Damit erhält man

$a=\dfrac {-\left( 11,11\,\frac {m}{s}\right )^{2}}{1,60\,m}=-77,16\,\frac {m}{s^{2}}$

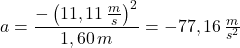
Die Bremsbeschleunigung beträgt also -77,16 m/s². Das entspricht dem 7,9-fachen der Erdbeschleunigung, also knapp 8 g.

Wirkende Kraft

Da für die Kraft gilt 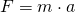$F=m\cdot a$ , beträgt auch die Kraft, die auf die Insassen wirkt, dem etwa dem 8-fachen ihrer Gewichtskraft.

Das kann u.U. bereits zu ernsthaften Verletzungen führen – vor allem wenn man nicht angeschnallt ist!

Wichtig dabei ist die Erkenntnis, dass die Beschleunigung und damit die auf die Insassen wirkende Kraft bei einem Unfall quadratisch mit der Geschwindigkeit steigt. Bei doppelter Geschwindigkeit (also 80 km/h) wären Beschleunigung und Kraft also 4-mal so groß und entsprächen über 31 g!

Welche Beschleunigung / wieviel g hält ein Mensch aus?

Diese Frage lässt sich nicht pauschal beantworten, da zum einen die Richtung der auftretenden Beschleunigungskräfte (längs oder quer zur Körperachse) wie auch die Dauer eine große Rolle spielen.

Menschen, die besonders hohen Beschleunigungskräften ausgesetzt sind, wie z.B. Kampfpiloten, Astronauten oder Rennfahrer, müssen ein spezielles Training absolvieren. Nicht alle Menschen sind dazu geeignet.

Für kurze Zeit (unterhalb von 0,5 s) können längs der Körperachse etwa 20 g ohne Folgeschäden überstanden werden.

Quer zum Körper kann man kurzzeitig etwa 30 g ertragen. Für einige Sekunden liegt die Grenze hier bei etwa 15 g.

Bei Achterbahnen liegt die Grenze des Erlaubten bei (kurzzeitig) 6 g, Astronauten müssen beim Start bis zu 5 g aushalten – das dann allerdings für einige Minuten!

Übungsaufgaben:

Cornelsen Oberstufe Physik Band 1 (1. Auflage 1997)

S. 27 A2, A3

S. 28 A10, A11, A13

weiter mit Überlagerung von Bewegungen

zurück zur Übersicht

Newton’sche Bewegungsgesetze