CD als Reflexionsgitter - Bestimmung der Spurweite einer CD

Warum schillern CDs und DVDs bunt?

Wenn man eine CD oder DVD im Licht betrachtet, fällt auf, dass diese bunt schillern.

Die Ursache dafür ist, dass CDs und DVDs wie ein optische Gitter wirken – es entstehen Interferenzmaxima, deren Lage von der Wellenlänge des Lichts abhängen. Dadurch erscheint die Oberfläche je nach Betrachtungswinkel in unterschiedlichen Farben.

Die digitalen Informationen auf einer CD oder DVD sind in einer spiralförmigen Spur gespeichert, die unterschiedlich lange Vertiefungen besitzt. Der Abstand der Spuren ist sehr klein und konstant, so dass die Oberfläche eine regelmäßige Struktur aufweist. Auf der anderen Seite der CD befindet sich die Reflexionsschicht, so dass die CD ein Reflexionsgitter darstellt.

Versuch:

Eine CD wird unter einem Winkel von ca. 60° mit einem Laser bestrahlt, so dass der Laserstrahl auf eine Stelle, die mittig zwischen dem Loch und dem Rand der CD liegt, trifft:

Auf einem Schirm bzw. an der Wand kann man mehrere Lichtflecke erkennen – ein Lichtpunkt, der das Hauptmaximum darstellt sowie weitere Lichtpunkte, bei denen es sich um Maxima höherer Ordnung handelt.

Auf dem rechten Bild sind nur das Hauptmaximum (unten) und das Maximum 1. Ordnung zu sehen.

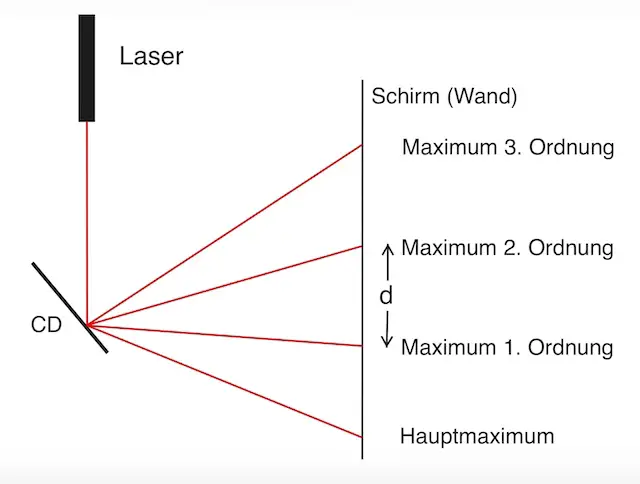
Für die Abstände der Maxima gelten die gleichen Bedingungen wie bei einem Transmissionsgitter. Die großen Abstände lassen bereits auf einen sehr kleinen Spurabstand schließen.

Bestimmung des Spurabstandes einer CD

Es gelten die Zusammenhänge

$\dfrac {k\cdot \lambda}{g}=sin\alpha$ ,

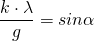wobei g der gesuchte Spurabstand ist und für den Abstand zweier benachbarter Maxima gilt: k = 1.

Außerdem gilt 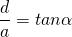$\dfrac {d}{a}=tan\alpha$

Dabei ist d der Abstand zwischen zwei benachbarten Maxima und a der Abstand zwischen CD (Auftreffpunkt des Lasers) und dem Schirm.

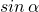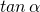Da a und d in der gleichen Größenordnung liegen und der Winkel α entsprechend groß ist, darf man $sin\, \alpha$ und $tan\, \alpha$ nicht gleichsetzen.

Man berechnet zunächst den Winkel 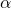$\alpha$ :

$tan\alpha=\dfrac {d}{a}=\dfrac {71cm}{122cm}=0,58$

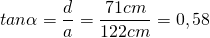
Damit ergibt sich 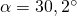$\alpha=30,2^{\circ}$

Nun stellt man die andere Gleichung nach g um und setzt diesen Winkel ein:

Mit 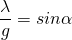$\dfrac {\lambda}{g}=sin\alpha$ ergibt sich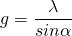 $g=\dfrac {\lambda}{sin\alpha}$

Werte einsetzen ergibt:

$g=\dfrac {6,35\cdot 10^{-7}m}{sin(30,2^{\circ})}=1,26\cdot 10^{-6}m=1,26\mu m$

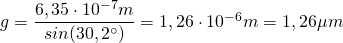
Da die CD schräg gegenüber dem Schirm steht, haben wir allerdings einen Fehler gemacht: In Wirklichkeit haben wir nicht den Spurabstand g bestimmt, sondern die Projektion des Spurabstandes unter dem Winkel 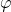$\varphi$ , den die CD zur Waagerechten steht. Dieser Abstand entspricht der Länge $g\cdot sin\varphi$ :

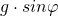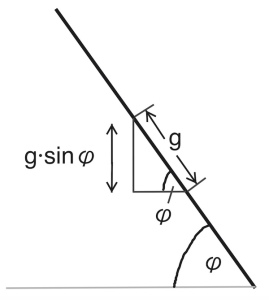
Somit müssen wir das Ergebnis von oben noch durch 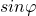$sin\varphi$ teilen.

Bei einem Winkel von 60° erhalten wir

$g=\dfrac {1,26\mu m}{sin(60^{\circ})}=1,45\mu m$

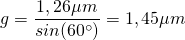
Ergebnis: Der Spurabstand einer CD beträgt 1,45μm.

Hinweis: Der tatsächliche Spurabstand beträgt 1,6μm.

CD als Transmissionsgitter

Einfacher und genauer ist die Bestimmung des Spurabstandes, wenn man die Reflexionsschicht von der CD entfernt. Dann lässt sich die CD als Transmissionsgitter verwenden, und die Korrektur über die Winkelbestimmung entfällt. Eine Messung ergibt einen Spurabstand mit sehr kleiner kleiner Abweichung des tatsächlichen Spruabstandes von 1,6μm.

weiter mit Interferenz am Einzelspalt

zurück