Gasgesetze und Gasgleichung

Die Gasgesetze

Während die Ausdehnung von Festkörpern und Flüssigkeiten bei Temperaturänderungen vergleichsweise gering sind, ist diese bei Gasen deutlich größer. Befindet sich ein Gas jedoch in einem abgeschlossenen Gefäß, so dass es sich nicht ausdehnen kann (das Volumen bleibt konstant), erhöht sich der Druck.

Die Größen Temperatur, Druck und Volumen hängen bei Gasen eng miteinander zusammen und werden auch als Zustandsgrößen bezeichnet.

Die Zusammenhänge zwischen diesen Zustandsgrößen sollen im Anschluss an die nachfolgende Definition des Drucks näher untersucht werden.

Der Druck

Ein in einem Behälter eingeschlossenes Gas übt auf alle Begrenzungsflächen des Behälters Kräfte aus. Um ein Gas zu komprimieren, muss man die Kraft auf eine oder mehrere Begrenzungsflächen erhöhen.

Beispiel:

Die Öffnung einer Luftpumpe wird zugehalten. Drückt man nun den Stempel weiter hinein, so benötigt man eine Kraft, die umso größer wird, je weiter man den Stempel hineindrückt.

Die Kraft F die man braucht, hängt außerdem von der Fläche A des Stempels ab. Je größer die Fläche des Stempels ist, umso größer ist die benötigte Kraft.

Der Quotient aus Kraft F und Fläche A wird als Druck p bezeichnet:

Der Druck

Der Quotient aus Kraft F und Fläche A wird als Druck p bezeichnet:

$p=\dfrac {F}{A}$

Die Einheit des Drucks ist $1\, \frac {N}{m^{2}}=1Pa$ (Pascal).

Gebräuchlich ist auch die Einheit Bar.

Es gilt:

1 bar = 10⁵ Pa = 1000 hPa (Hektopascal)

und damit

1 mbar = 1 hPa

Um den Zusammenhang zwischen den Größen Temperatur, Druck und Volumen eines Gases zu untersuchen, wird jeweils eine Größe konstant gehalten und das Verhalten einer bestimmten (gleichbleibenden) Gasmenge untersucht. Die Ergebnisse werden in Form von einzelnen Gesetzen formuliert.

Zusammenhang zwischen Temperatur T und Volumen V (p = konst.)

Diesen Zusammenhang haben wir bereits zur Überlegung zum absoluten Nullpunkt verwendet:

Bei konstantem Druck ist die Volumenänderung $\Delta V$ fast aller Gase proportional zur Temperaturänderung $\Delta \vartheta$ .

Bei Verwendung der absoluten Temperaturskala gilt:

Bei konstantem Druck ist das Volumen eines (idealen*) Gases proportional zur Temperatur.

Dieses Gesetz wurde nach dem französischen Chemiker und Physiker Joseph Louis Gay-Lussac benannt:

Gesetz von Gay-Lussac

Bei konstantem Druck sind Temperatur und Volumen zueinander proportional:

$V \sim T$

bzw.

$\dfrac {V_{1}}{T_{1}}=\dfrac {V_{2}}{T_{2}}$ oder $\dfrac {V}{T}=konst.$

Zusammenhang zwischen Druck p und Volumen V (T = konst.)

Das in einem Zylinder eingeschlossene Gas wird durch Erhöhung des Drucks komprimiert. Dadurch sinkt das Volumen, und das Gas erwärmt sich.

Um die Temperatur konstant zu halten, muss die Kompression so langsam stattfinden, dass sich das Gas durch Wärmeaustausch mit der Umgebung praktisch nicht erwärmt, oder man wartet nach der Kompression, bis das Gas wieder seine Ausgangstemperatur erreicht hat und bestimmt dann jeweils Druck und Volumen.

Die Auswertung der Messergebnisse für Druck und Volumen ergeben das nach Robert Boyle und Edme Mariotte benannte Gesetz:

Gesetz von Boyle-Mariotte

Bei konstanter Temperatur ist das Volumen umgekehrt proportional zum Druck:

Es gilt:

$p\sim \dfrac {1}{V}$

Dieser Zusammenhang lässt sich auch anders ausdrücken:

Bei konstanter Temperatur ist das Produkt aus Druck und Volumen konstant:

$p\cdot V=konst.$

Damit gilt: $p_{1}V_{1}=p_{2}V_{2}$

Zusammenhang zwischen Temperatur und Druck (V = konst.)

Befindet sich ein Gas in einem abgeschlossenen Gefäß bei konstantem Volumen, so steigt der Druck proportional mit der Temperatur.

Gesetz von Amontons

Bei konstantem Volumen sind Temperatur und Druck zueinander proportional:

$p\sim T$

bzw.

$\dfrac {p}{T}=konst.$ bzw. $\dfrac {p_{1}}{T_{1}}=\dfrac {p_{2}}{T_{2}}$

Alle Gasgesetze gelten streng genommen nur für ideale Gase.

* Ideales Gas

Unter einem idealen Gas versteht man die Modellvorstellung eines realen Gases mit folgenden Eigenschaften:

Die Gasteilchen sind punktförmig und ohne Ausdehnung (ohne Volumen).
Alle Gasteilchen bewegen sich frei, bis sie auf ein anderes Gasteilchen oder auf die Gefäßwand treffen.
Es gibt keine Anziehungskräfte zwischen den Gasteilchen.
Alle Wechselwirkungen untereinander sowie mit der Gefäßwand sind elastische Stöße; es gilt Impuls- und Energieerhaltung.

Bei ausreichend geringen Dichten, also bei nicht zu hohen Drücken und nicht zu niedriger Temperatur, lassen sich diese Gesetze aber auch auf reale Gase mit guter Genauigkeit anwenden.

Die Allgemeine Gasgleichung

Aus den drei Gasgesetzten folgt die allgemeine Gasgleichung:

Allgemeine Gasgleichung

Für eine abgeschlossene Menge eines idealen Gases ist bei allen Zustandsänderungen der Quotient $\dfrac {pV}{T}$ konstant:

Es gilt:

$\dfrac {p_{1}\, V_{1}}{T_{1}}=\dfrac {p_{2}\, V_{2}}{T_{2}}$

bzw.

$\dfrac {p\cdot V}{T}=konst.$

Die Gasgesetze von Gay-Lussac, Amontons und Boyle-Mariotte sind letztendlich Spezialfälle der allgemeinen Gasgleichung.

Zustandsänderungen

Für thermodynamische Zustandsänderungen, bei denen eine der Zustandsgrößen konstant bleibt, gibt es besondere Bezeichnungen:

Ist der Druck konstant (p = konst.), spricht man von einer isobaren Zustandsänderung.

Ist das Volumen konstant (V = konst.), spricht man von einer isochoren Zustandsänderung.

Ist die Temperatur konstant (T = konst.), spricht man von einer isothermen Zustandsänderung.

Auf der Webseite von Walter Fendt findet man Simulationen zu allen drei genannten Zustandsänderungen, mit der die Gasgesetze überprüft werden können.

Darstellung von Zustandsänderungen in Diagrammen

Trägt man die beiden sich ändernden Zustandsgrößen für die oben genannten Spezialfälle gegeneinander auf, so ergeben sich folgende Diagramme:

isobare

Zustandsänderung

isochore

Zustandsänderung

isotherme

Zustandsänderung

Beispielaufgaben zu den Gasgesetzen

Der erste Schritt bei der Lösung von Aufgaben zu den Gasgesetzen ist es zu ermitteln, welche der drei Zustandsgrößen konstant bleibt, also welche Art von Zustandsänderung vorliegt. Daraus ergibt sich dann, welches der Gasgesetze angewandt werden kann.

Aufgabe 1:

Bei einer Temperatur von 18 °C beträgt der Druck in einem Autoreifen 220 kPa.

Das Auto steht auf einem Parkplatz in der Sonne. Dadurch erhöht sich die Temperatur im Reifen auf 55 °C.

Frage: Auf welchen Wert vergrößert sich der Reifendruck?

Vorüberlegung:

Gegeben sind folgende Größen:

$\vartheta_{1}=18\, ^{\circ}C$

$\vartheta_{2}=55\, ^{\circ}C$

$p_{1}=220\, kPa$

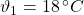
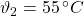
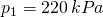
Gesucht ist 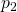$p_{2}$

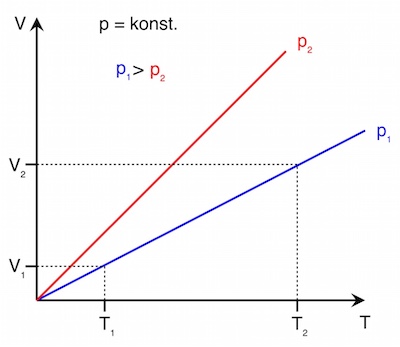
In diesem Beispiel ändern sich Temperatur T und Druck p. Das Volumen V eines Autoreifens ist jedoch unabhängig vom Druck weitgehend konstant.

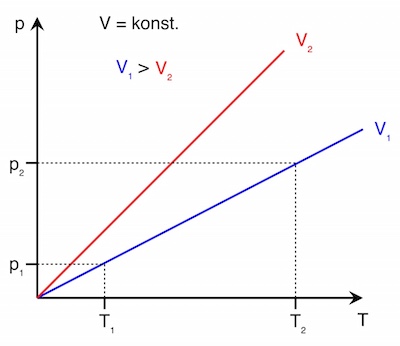
Es gilt also V = konst.

Damit handelt es sich annähernd um eine isochore Zustandsänderung, und es lässt sich das Gesetz von Amontons anwenden:

Es gilt also:

$\dfrac {p_{1}}{T_{1}}=\dfrac {p_{2}}{T_{2}}$

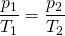
Gesucht ist in diesem Beispiel p₂(s.o.). Umstellen der Gleichung nach p₂ ergibt:

$p_{2}=T_{2}\cdot \dfrac {p_{1}}{T_{1}}$

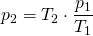
Nun werden die Werte eingesetzt.

Wichtig dabei ist, dass man alle Werte in den Basiseinheiten einsetzt, also

Temperaturen in Kelvin: T₁ = 291,15 K, T₂ = 328,15 K

Druck in Pascal: p₁ = 220.000 Pa

Damit ergibt sich:

$p_{2}=328,15\, K\cdot \dfrac {220\,000\,Pa}{291,15\, K}$

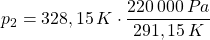
Das Ergebnis lautet:

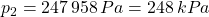$p_{2}=247\,958\, Pa=248\, kPa$ (Das sind 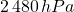$2\,480\, hPa$ oder $2,48\, Bar$ )

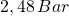Aufgabe 2:

Wie viel Luft entweicht aus einem quaderförmigen Raum mit 10 m Länge, 6 m Breite und 4 m Höhe, wenn die Raumtemperatur von 12 °C auf 20 °C erhöht wird und der Luftdruck konstant bleibt?

Vorüberlegung:

Gegeben sind folgende Größen:

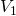$V_{1}$ → kann aus den Abmessungen des Raumes berechnet werden:

$V_{1}=10\, m\cdot 6\, m\cdot 4\, m=240\, m^{3}$

$\vartheta_{1}=12\, ^{\circ}C$

$\vartheta_{2}=20\, ^{\circ}C$

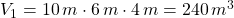
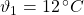
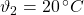
Gesucht ist die Volumenänderung ΔV = V₂ – V₁. Da V₁ bekannt ist (s.o.), muss also zunächst V₂ berechnet werden.

Da der Luftdruck konstant bleibt (p = konst.), handelt es sich um eine isobare Zustandsänderung.

Damit lässt sich das Gesetz von Gay-Lussac anwenden:

Es gilt:

$\dfrac {V}{T}=konst.$

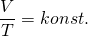
bzw.

$\dfrac {V_{1}}{T_{1}}=\dfrac {V_{2}}{T_{2}}$

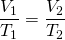
Nun stellen wir diese Gleichung nach V₂ um

$V_{2}=\dfrac {V_{1}\cdot T_{2}}{T_{1}}$

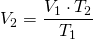
und setzen die Werte ein (alle Werte in Basiseinheiten umrechnen!):

$V_{2}=\dfrac {240\, m^{3}\cdot 293,15\, K}{285,15\, K}=246,73\, m^{3}$

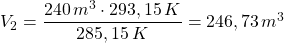
Nun muss noch die Volumenänderung berechnet werden:

$\Delta V=V_{2}-V_{1}=246,73\, m^{3}-240\, m^{3}=6,73\, m^{3}$

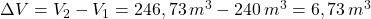
Antwort: Es entweichen 6,73 m³ Luft aus dem Raum.

Aufgabe 3:

Wie viel Luft entweicht aus dem Raum der vorherigen Aufgabe, wenn gleichzeitig der Luftdruck von 1020 mbar auf 981 mbar sinkt?

Vorüberlegung:

Zusätzlich zu den in Aufgabe 2 genannten Größen gilt:

$p_{1}=1\,020\, mbar$

$p_{2}=981\, mbar$

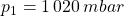
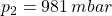
Da sich nun alle drei Zustandsgrößen ändern, liegt kein Spezialfall vor. Es reicht also nicht aus, nur eines der Gasgesetze anzuwenden.

Da der Druck kleiner wird, ist zu erwarten, dass mehr Luft entweichen wird als in Aufgabe 2.

Da sich alle Zustandsgrößen ändern, kann man die Allgemeine Gasgleichung benutzen. Diese lautet:

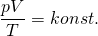$\dfrac {pV}{T}=konst.$ bzw. $\dfrac {p_{1}\, V_{1}}{T_{1}}=\dfrac {p_{2}\, V_{2}}{T_{2}}$

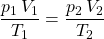
Gesucht ist wieder die Volumenänderung, also zunächst V₂.

Die allgemeine Gasgleichung muss also nach V₂ umgestellt werden:

$V_{2}=V_{1}\cdot \dfrac {T_{2}\cdot p_{1}}{T_{1}\cdot p_{2}}$

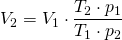
Nun werden die Werte eingesetzt (Basiseinheiten!*):

$V_{2}=240\, m^{3}\cdot \dfrac {293,15\, K\cdot 102\,000\, Pa}{285,15\, K\cdot 98\,100\,Pa}=256,54\, m^{3}$

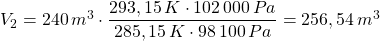
* Hinweis:

In diesem Fall hätte man die Einheit des Drucks auch bei mbar belassen können, da sich die Einheit wegkürzt und das Verhältnis 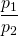$\dfrac {p_{1}}{p_{2}}$ unabhängig von der Einheit ist. Das gilt jedoch nicht für die Temperatur! Hier muss immer die absolute Temperatur eingesetzt werden.

Nun muss noch die Volumenänderung berechnet werden:

$\Delta V=V_{2}-V_{1}=256,54\, m^{3}-240\, m^{3}=16,54\, m^{3}$

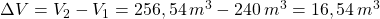
Antwort: In diesem Fall entweichen 16,54 m³ Luft aus dem Raum.

Wie erwartet ist die entweichende Luftmenge größer als beim konstantem Druck in Aufgabe 2.

Alternative Lösung ohne Allgemeine Gasgleichung

Eine alternative Lösung ohne die allgemeine Gasgleichung anzuwenden ist möglich, wenn man sich überlegt, dass es keine Rolle spielt, ob sich Temperatur und Druck gleichzeitig oder nacheinander ändern.

Da wir in Aufgabe 2 bereits die Volumenänderung durch die Temperaturerhöhung berechnet haben, lässt sich in einem zweiten Schritt die Volumenänderung durch die Druckverminderung bei der konstanten Temperatur von 20 °C berechnen:

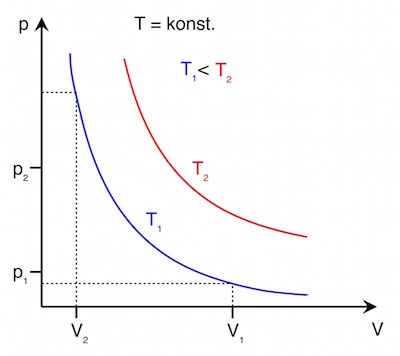
Nimmt man also an, dass die Temperaturerhöhung bereits abgeschlossen ist und sich nun anschließend der Druck ändert, liegt eine isotherme Zustandsänderung vor, und es lässt sich das Gesetz von Boyle-Mariotte anwenden:

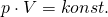$p\cdot V=konst.$ bzw. $p_{1}\cdot V_{1}=p_{2}\cdot V_{2}$

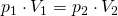
Umgestellt nach V₂ ergibt sich:

$V_{2}=\dfrac {p_{1}}{p_{2}}\cdot V_{1}$

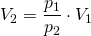
Einsetzen der Werte liefert

$V_{2}=\dfrac {1020}{981}\cdot 246,73\, m^{3}=256,54\, m^{3}$

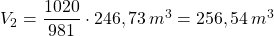
(Die Einheiten beim Druck kürzen sich weg, für V₁ muss hier das Volumen nach der Temperaturänderung eingesetzt werden.)

Wir erhalten also auch auf diese Weise das gleiche Ergebnis für V₂ wie mit der allgemeinen Gasgleichung!

weiter mit Universelle Gasgleichung

zurück