Die kinetische Gastheorie

Wie im letzten Abschnitt beschrieben befinden sich die Atome oder Moleküle in Gasen in ständiger ungeordneter Bewegung, wobei die Bewegungsenergie von der Temperatur des Gases abhängt.

Die universelle Gasgleichung zeigt, dass das thermische Verhalten aller Gase nahezu identisch ist. Das lässt sich mit der kinetischen Gastheorie durch einfache Annahmen mit Hilfe der Gesetze der Mechanik erklären.

Mit den Eigenschaften von Gasen, dass die einzelnen Atome bzw. Moleküle gegenüber Flüssigkeiten und Festkörpern sehr weit voneinander entfernt sind (die Dichte von Gasen etwa 1000-mal geringer als die der Flüssigkeiten) und damit der Abstand der Teilchen wesentlich größer ist als ihr Durchmesser, sind die Kräfte, die die Gasteilchen aufeinander ausüben, verschwindend gering.

Nur bei Stößen untereinander gibt es Abstoßungen.

Grundannahmen der kinetischen Gastheorie

Die Grundannahmen der kinetischen Gastheorie ähneln der Theorie des idealen Gases.

Der Durchmesser der Gasmoleküle bzw. -atome ist sehr viel kleiner als ihre gegenseitigen Abstände.
Die Gasteilchen üben nur im Augenblick des Zusammenstoßes Kräfte aufeinander aus.
Die Stöße zwischen den Gasteilchen und der Gefäßwand sind elastisch
Die Bewegung der Gasteilchen erfolgt völlig regellos und ungeordnet.

Die kinetische Gastheorie beschreibt die räumliche Verteilung der Gasteilchen sowie ihre Geschwindigkeitsverteilung.

Die Gasteilchen in einem abgeschlossenen Behälter bewegen sich alle unterschiedlich schnell. Bei jedem Stoß mit einem anderen Teilchen kann sich die Geschwindigkeit ändern. Je höher die Temperatur des Gases ist, umso größer wird die mittlere Geschwindigkeit der Gasteilchen.

Da alle Gasteilchen ständig in Bewegung sind, nehmen Gase stets den gesamten zur Verfügung stehenden Raum ein.

Für die räumliche Verteilung gilt:

Die Gleichverteilung ist die wahrscheinlichste räumliche Anordnung in einem gegebenen Raumbereich:

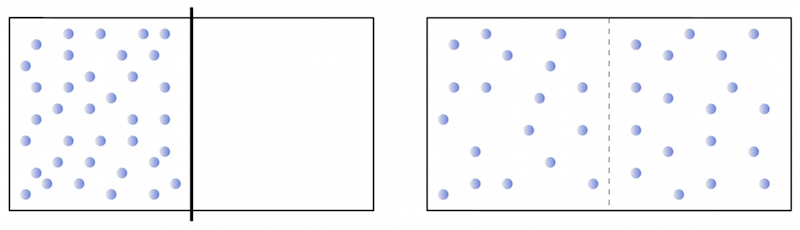
Befindet sich im linken Bereich ein (ideales) Gas, welches vom rechten Bereich durch eine Trennwand getrennt ist, so verteilen sich die Gasteilchen nach Beseitigung der Trennwand in kurzer Zeit gleichmäßig im gesamten zur Verfügung stehenden Raumbereich.

Die Teilchenzahldichte ist in allen Raumbereichen annähernd konstant.

Für die Geschwindigkeitsverteilung gilt:

Die Teilchen eines Gases haben unterschiedliche Geschwindigkeiten.

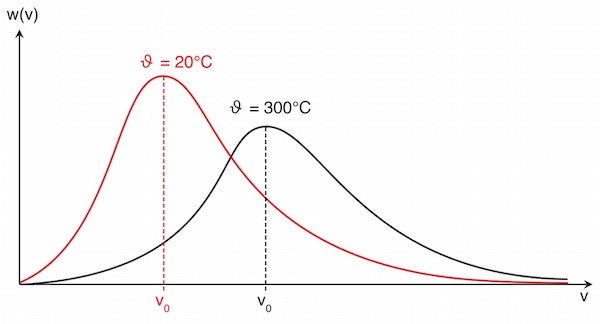
Die Geschwindigkeitsverteilung ist temperaturabhängig. Folgende Abbildung zeigt die Geschwindigkeitsverteilung der Teilchen eines Gases bei zwei unterschiedlichen Temperaturen:

Bei steigender Temperatur verschiebt sich das Maximum der Funktion immer mehr zu höheren Geschwindigkeiten.

Für jede Temperatur gibt es eine häufigste Geschwindigkeit $v_{0}$ sowie eine mittlere Geschwindigkeit $\overline v$ der Gasteilchen. Damit lässt sich die mittlere kinetische Energie $\overline {E}_{kin}$ der Gasteilchen berechnen:

$\overline {E}_{kin}=\frac {1}{2}\, m\, \overline v^{2}$

Zusammenhang zwischen Druck und mittlerer kinetischer Energie

Der Druck eines abgeschlossenen Gases auf die Gefäßwand ist eine Folge der beim Aufprall vieler Teilchen übertragenen Impulse.

Mit Hilfe des Impulserhaltungssatzes erhält man mit einer recht einfachen Berechnung folgenden Zusammenhang zwischen dem Druck in einem idealen Gas und der mittleren kinetischen Energie $\overline {E}_{kin}$ der Moleküle.

Die Grundgleichung der kinetischen Gastheorie lautet:

$p\cdot V=\frac {2}{3}\, N\cdot \overline {E}_{kin}$

bzw.

$p=\dfrac {2}{3}\, \dfrac {N}{V}\cdot \overline {E}_{kin}$

Wie schnell sind die Gasteilchen?

Aus der Grundgleichung der kinetischen Gastheorie ergibt sich der Zusammenhang

$p\cdot V=\frac {2}{3}\, N\cdot \frac {1}{2}\, m\, \overline v^{2}$

Dabei ist $m$ die Masse eines Gasteilchens. Daraus folgt

$p=\dfrac {1}{3}\, \dfrac {N\cdot m}{V}\cdot \overline v^{2}$

Das Produkt $N\cdot m$ ist die Masse des Gases, damit ist der Quotient $\dfrac {N\cdot m}{V}$ die Dichte ρ des Gases.

Damit erhält man:

$p=\frac {1}{3}\, \rho\, \overline v^{2}$

Durch Umstellen der Gleichung erhält man die mittlere Geschwindigkeit der Teilchen in einem idealen Gas:

$\overline {v}=\sqrt {\dfrac {3\, p}{\rho}}$

Für Luft ( $\rho=1,293\, \frac {kg}{m^{3}}$ ) ergibt sich bei Normalbedingungen ein Wert von

$\overline {v}=482\, \frac {m}{s}$

Dieser Wert erscheint sehr hoch. Dabei darf man aber nicht vergessen, dass die Gasteilchen nur sehr kurze Strecken auf geradem Weg zurücklegen, da sie ständig miteinander kollidieren. Die Gasteilchen kommen also letztendlich nicht weit.

Die mittlere freie Weglänge der Gasteilchen liegt in einer Größenordnung von 10^-7m! Jedes Gasteilchen stößt dabei ca. 10¹⁰-mal pro Sekunde (!) mit einem anderen Gasteilchen zusammen.

Temperatur und mittlere kinetische Energie

Die Temperatur ist ein Maß für die mittlere kinetische Energie aller Moleküle. Je größer die Temperatur, umso größer die mittlere kinetische Energie.

Aus der Grundgleichung der kinetischen Gastheorie (s.o.) und der universellen Gasgleichung ergibt sich:

$p\cdot V=\dfrac {2}{3}\, N\cdot \overline E_{kin}=N\cdot k\cdot T$ und damit $\overline {E}_{kin}=\dfrac {3}{2}\, k\cdot T$

Die mittlere kinetische Energie eines Teilchens und die absolute Temperatur eines Gases sind zueinander proportional:

$\overline {E}_{kin}=\dfrac {3}{2}\, k\cdot T$

(Dabei ist k die Boltzmann-Konstante.)

weiter mit Erster Hauptsatz der Thermodynamik

zurück

Kinetische Gastheorie