Die Magnetische Feldstärke

Messgröße für die Stärke des magnetischen Feldes

Analog zur elektrischen Feldstärke soll nun eine geeignete Messgröße für die Stärke von Magnetfeldern gefunden werden. Dazu erinnern wir uns zunächst an die elektrische Feldstärke:

Die elektrische Feldstärke ist definiert als Kraft pro Ladung: $E=\dfrac {F}{Q}$

Während in einem elektrischen Feld eine Kraft auf Ladungen bzw geladene Körper wirkt, gibt es im Magnetfeld eine Kraftwirkung auf

ferromagnetische Stoffe

Magnete

bewegte Ladungen

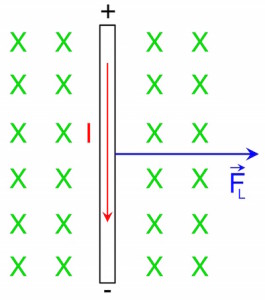
Betrachten wir das Experiment mit dem rollenden Stab oder der Leiterschaukel etwas genauer:

Die technische Stromrichtung (roter Pfeil) verläuft von oben (+) nach unten (-), die Elektronen fließen also von unten nach oben.

Das Magnetfeld zeigt in die Zeichenebene hinein. Das wird durch die grünen Kreuze dargestellt.

Aus der Dreifingerregel ergibt sich, dass die Lorentzkraft nach rechts zeigt.

Wovon hängt die Größe der Lorentzkraft ab?

Für die Kraft, die auf den Leiter wirkt, gelten folgende Zusammenhänge:

Die Kraft auf den Leiter ist umso größer,

je größer die Stromstärke I im Leiter ist

je länger der stromdurchflossene Leiter ist (ansonsten müssten unterschiedlich lange Leiter verschieden stark abgelenkt werden)

Die magnetische Feldstärke

Genaue Messungen ergeben:

Die Kraft 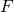$F$ ist proportional zur Stromstärke $I$ : $F\sim I$
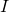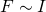
Die Kraft 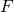$F$ ist proportional zur Länge $s$ des Leiters: 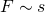$F\sim s$

Die beiden Proportionalitäten lassen sich zusammenfassen.

Dadurch ergibt sich: $F\sim I\cdot s$ bzw. $\dfrac {F}{I\cdot s}=konst.$

Die Konstante $\dfrac {F}{I\cdot s}$ hängt nicht von der Länge des Leiters oder der Stromstärke ab, sondern nur von der Stärke des Magnetfeldes.

In einem stärkeren Magnetfeld ist der Quotient (und damit die Kraft) bei gleicher Stromstärke und Leiterlänge größer, in einem schwächeren kleiner.

Daher ist es sinnvoll, diese Konstante als Maß für die Stärke des Magnetfeldes zu verwenden. Aus historischen Gründen wird sie als magnetische Flussdichte oder magnetische Induktion bezeichnet und hat das Formelzeichen B.

In einigen Büchern und auch im Zentralabitur in Bremen wird sie jedoch als magnetische Feldstärke bezeichnet, obwohl die magnetische Feldstärke offiziell anders festgelegt ist. Beachte dazu den unten stehenden Hinweis*!

Die magnetische Flussdichte

Die magnetische Flussdichte B gibt an, wie stark ein Magnetfeld ist:

$B=\dfrac {F}{I\cdot s}$

Die Einheit der magnetischen Flussdichte heißt Tesla (T)

$1\, T=1\; \dfrac {N}{Am}$

Alle Schüler aus Bremen oder anderen Bundesländern, in denen die magnetische Flussdichte als magnetische Feldstärke bezeichnet wird, können sich an folgende Definition halten, die auch bei den nachfolgenden Beispielen und Berechnungen verwendet wird:

Die magnetische Feldstärke

Die magnetische Feldstärke B gibt an, wie stark ein Magnetfeld ist:

$B=\dfrac {F}{I\cdot s}$

Die Einheit der magnetischen Feldstärke heißt Tesla (T)

$1\, T=1\; \dfrac {N}{Am}$

*Hinweis:

Aus historischen Gründen bezeichnet man die Größe B laut Ausführungsverordnung zum Gesetz über Einheiten im Messwesen (1970) als magnetische Flussdichte oder magnetische Induktion.

International werden jedoch die Bezeichnungen magnetisches Feld und magnetische Feldstärke benutzt. Diese Bezeichnung findet man inzwischen auch in mehreren Schulbüchern (z.B. Metzler Physik). Außerdem wird diese Bezeichnung in einigen Bundesländern im Zentralabitur verwendet.

Die offizielle Größe “magnetische Feldstärke” hat das Formelzeichen H und ist mit der magnetischen Flussdichte B über die magnetische Feldkonstante $\mu_{0}$ folgendermaßen verknüpft:

Magnetische Flussdichte $B=\mu_{0}H$ Einheit: Tesla ( $T$ )

bzw.

Magnetische Feldstärke $H=\dfrac {B}{\mu_{0}}$ Einheit: $\dfrac {A}{m}$

Berechnung der Kraft auf einen stromdurchflossenen Leiter

Die Kraft auf einen stromdurchflossenen Leiter der Länge $s$ in einem Magnetfeld der Stärke $B$ beträgt damit:

$F=B\cdot I\cdot s$ für den Fall, dass $I$ und $B$ senkrecht aufeinander stehen

Ansonsten gilt:

$F=B\cdot I\cdot s\cdot sin\alpha$

Sowohl die Kraft $F$ als auch der Strom $I$ und die Magnetische Feldstärke $B$ sind Vektorgrößen. Man verwendet daher auch die vektorielle Schreibweise. Sie lautet:

$\overrightarrow {F}=s\left( \overrightarrow {B}\times \overrightarrow {I}\right)$

Der Vektor $\overrightarrow {B}$ zeigt in Richtung der magnetischen Feldlinien.

Info:

Das Vektorprodukt (Kreuzprodukt):

Es gilt: $\left| \overrightarrow {c}\right| =\left| \overrightarrow {a}\right|\cdot \left| \overrightarrow {b}\right|$ $\Leftrightarrow$ $\overrightarrow {c}=\overrightarrow {a}\times \overrightarrow {b}$

$\overrightarrow {c}$ steht dabei senkrecht zu $\overrightarrow {a}$ und $\overrightarrow {b}$ .

Geometrisch lässt sich das so deuten:

Der Betrag von $\overrightarrow {c}$ ist der Flächeninhalt des von $\overrightarrow {a}$ und $\overrightarrow {b}$ aufgespannten Parallelogramms.

Beispiel zur Berechnung der Magnetfeldstärke

In einem Magnetfeld befindet sich ein Leiter mit der Länge s = 0,1 m.

Im Leiter fließt ein Strom der Stärke I = 3 A.

Wie groß ist die magnetische Feldstärke, wenn auf den Leiter eine Kraft von F = 22 mN wirkt?

Lösung:

Die magnetische Feldstärke beträgt

$B=\dfrac {F}{I\cdot s}=\dfrac {0,022\, N}{3\, A\cdot 0,1\, m}=0,073\, T=\, 73mT$ .

Beispiele für magnetische Feldstärken in der Praxis:

Hufeisenmagnet	bis 0,2 T
MRT	bis 3 T
Erdmagnetfeld	2 · 10^-5 T
Elektromagnet	bis 20 T

Info:

Inzwischen ist es möglich, Magnetfelder mit einer Stärke von über 100 T zu erzeugen. Derartig hohe Feldstärken sind jedoch nur kurzzeitig realisierbar und nicht für normale Elektromagneten nutzbar.

Der stärkste Magnet der Welt, der sein Magnetfeld über längere Zeit aufrecht erhalten kann, erzeugt ein Magnetfeld von 45 T. Bei diesem Supermagneten handelt es sich um eine Kombination aus Elektro- und Permanentmagnet.

Ein interessantes Video dazu findest Du im YouTube-Kanal von Veritasium: World’s Strongest Magnet!

weiter mit Kraft auf Ladungsträger im Magnetfeld

zurück