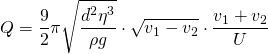Der Millikan-Versuch zur Bestimmung der Elementarladung

Der Millikan-Versuch – Bestimmung der Elementarladung

In der Mitte des 19. Jahrhunderts fand MICHAEL FARADAY (1791–1867) heraus, dass bei der Elektrolyse zur Abscheidung einer bestimmten Anzahl von Atomen gegebener Wertigkeit immer die gleiche Ladung erforderlich ist. Auf dieser Grundlage versuchte der britische Physiker G. J. STONEY (1826–1911) eine erste Abschätzung der Elementarladung, konnte aber nur einen statistischen Mittelwert angeben.

Mit einem völlig anderen Verfahren gelang es dem amerikanischen Physiker ROBERT ANDREWS MILLIKAN (1868–1953) in den Jahren 1909 bis 1913 erstmals, die Elementarladung e relativ genau zu bestimmen. Er nutzte dazu die Tröpfchenmethode, der Versuch wird heute als MILLIKAN-Versuch (oder auch Öltröpfchenversuch) bzw. MILLIKAN-EXPERIMENT bezeichnet. MILLIKAN erhielt für die Präzisionsmessung der Elementarladung 1923 den Nobelpreis für Physik.

Zuvor war gar nicht klar, ob es überhaupt so etwas wie eine kleinste Ladung gibt.

Mit dem im folgenden beschriebenen Experiment konnte Robert Millikan nachweisen, dass es eine kleinste Ladung – die sog. Elementarladung – gibt, und er konnte diese als erster relativ genau bestimmen.

Grundgedanke und Versuchsaufbau zum Millikan-Versuch

Wenn man Öl zerstäubt, erhält man winzige Tröpfchen, die durch den Vorgang des plötzlichen Teilens elektrisch geladen werden (positiv oder negativ).

Ein Öltröpfchen fällt unter dem Einfluss der Schwerkraft nach unten, wird aber durch die Reibung in der Luft abgebremst, so dass die Fallgeschwindigkeit klein bleibt – genauso, wie sehr feine Regentropfen nur sehr langsam nach unten fallen.

Die Reibungskraft ist von der Geschwindigkeit abhängig. Je größer die Fallgeschwindigkeit wird, umso größer ist die Reibungskraft. Ist die Reibungskraft so groß wie die Gewichtskraft, heben sich beide Kräfte auf, und das Tröpfchen wird nicht weiter beschleunigt, sondern bewegt sich mit konstanter Geschwindigkeit weiter.

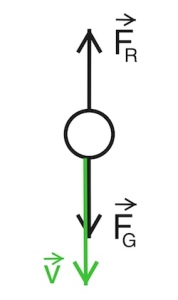
Öltröpfchen beim Fallen in Luft (ohne elektrisches Feld):

Nach einer sehr kurzen Beschleunigungsphase führt das Öltröpfchen eine gleichförmige Bewegung aus (v₀ = konst.), da sich die Gewichtskraft F_G und die Reibungskraft F_R aufheben.

Es herrscht dann ein Kräftegleichgewicht:

|F_G| = |F_R|

(Die Reibungskraft in Luft hängt von der Geschwindigkeit ab – je größer v, desto größer F_R).

Die Reibungskraft F_R für einen kugelförmigen Körper in einem Medium der Zähigkeit (dynamische Viskosität) η (Eta) beträgt:

$F_ {R}=6\, \pi\, \eta\, r\, v$ (Dabei ist $r$ der Radius des kugelförmigen Körpers)

Die Reibungskraft steigt also proportional zur Geschwindigkeit.

Dieser Zusammenhang wird als Stokessches Gesetz bezeichnet.

Für Luft gilt: $\eta=1,82\cdot 10^{-5}\frac {kg}{ms}$

Wie bei Regentropfen gilt:

Je schwerer der Tropfen ist (je größer die Gewichtskraft F_G), umso größer ist die Fallgeschwindigkeit v und damit auch die Reibungskraft F_R.

Daher kann man aus der Fallgeschwindigkeit auf die Gewichtskraft eines Öltröpfchens schließen.

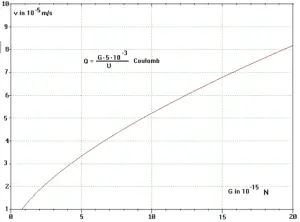
Ein vereinfachter Zusammenhang zwischen Fallgeschwindigkeit und Gewichtskraft ist in folgendem Diagramm dargestellt:

^{Zusammenhang zwischen Fallgeschwindigkeit v und Gewichtskraft FG eines Öltröpfchens in Luft}

Man erkennt im Diagramm:

Bis zu einer bestimmten Masse bzw. Gewichtskraft schwebt das Öltröpfchen.

(Vgl.: bei Nebel sind die Tröpfchen so klein, dass sie in der Luft stehen und nicht herunterfallen.)

Öltröpfchen im elektrischen Feld

Befindet sich das geladene Öltröpfchen zusätzlich in einem elektrischen Feld, wirkt eine weitere Kraft, nämlich die elektrische Kraft:

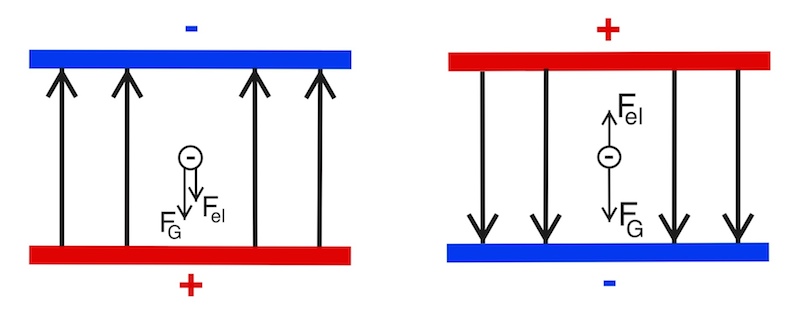
Je nach Richtung des elektrischen Feldes bzw. je nach Vorzeichen der elektrischen Ladung des Öltröpfchens wirken Gewichtskraft F_Gund elektrische Kraft F_el entweder in die gleiche (linkes Bild) oder in entgegengesetzte Richtung (rechtes Bild).

Die elektrische Kraft hängt von der Ladung Q des Öltröpfchens sowie der elektrischen Feldstärke E und damit von der angelegten Spannung U ab.

Sind elektrische Kraft und Gewichtskraft gleich groß und entgegengesetzt, herrscht ein Kräftegleichgewicht, und das Öltröpchen schwebt.

Für den Schwebezustand gilt:

$F_ {G}=F_ {el}$

Mit $F_ {el}=E\cdot Q$ und $E=\dfrac {U}{d}$

ergibt sich für die Ladung des Öltröpfchens

$Q=\dfrac {F_{G}\cdot d}{U}$

Ist die Gewichtskraft bekannt, so kann die Ladung eines Öltröpfchens mit dieser Gleichung leicht berechnet werden.

Mit Hilfe des oben dargestellten Zusammenhangs lässt sich die Gewichtskraft eines Öltröpfchens aus der (messbareren) Fallgeschwindigkeit ohne elektrisches Feld abschätzen. Allerdings ist diese Methode recht ungenau, da der dargestellte Zusammenhang eine Vereinfachung darstellt.

Doch auch ohne die Gewichtskraft zu kennen, ist es möglich, die Ladung eines Öltröpfchens zu bestimmen.

Die Bestimmung der Ladung eines Öltröpfchens mit Hilfe des Millikan-Versuchs lässt sich grundsätzlich mit Hilfe zweier verschiedener Methoden durchführen:

Methode 1: Schwebemethode

Diese Methode beruht auf der Bestimmung der Ladung durch Messen der Schwebespannung und der Fallgeschwindigkeit ohne elektrisches Feld.

Vorgehensweise:

Ein Öltröpfchen wird durch Änderung der Spannung zum Schweben gebracht (s.o.). Diese sog. “Schwebespannung” wird notiert. Im Schwebezustand gibt es ein Kräftegleichgewicht zwischen Gewichtskraft und elektrischer Kraft.

Es gilt: $F_{el}=F_{G}$ .

Anschließend wird die Spannung ausgeschaltet und die Fallgeschwindigkeit dieses Öltröpfchens ohne elektrisches Feld gemessen. Dabei stellt sich ein Kräftegleichgewicht zwischen Gewichtskraft und Reibungskraft ein.

Es gilt: $F_{G}=F_{R}$ .

Für den Schwebezustand gilt:

$F_ {el}=F_ {G}$ mit $F_ {G}=mg$

mit $m=\rho V$ und $V_ {Kugel}=\frac {4}{3}\pi r^{3}$

erhält man:

$QE=\rho \frac {4}{3}\pi r^{3}g$

mit $E=\dfrac {U}{d}$ ergibt sich:

$Q=\dfrac {4\rho d\pi r^{3}g}{3U}$ (1)

Für den Fall im Gravitationsfeld gilt:

$F_ {G}=F_ {r}$

$\rho \cdot \frac {4}{3}\pi r^{3}g=6\pi r\eta v$

aufgelöst nach r ergibt sich:

$r=\sqrt {\dfrac {9\eta v}{2\rho g}}$ (2)

Der Radius $r$ des Öltröpfchens ist praktisch nicht bestimmbar.

Indem man (2) in (1) einsetzt, lässt sich der Radius jedoch eliminieren. Man erhält so:

$Q=\dfrac {6\pi d\eta v}{U}\cdot \sqrt {\dfrac {9\eta v}{2\rho g}}$

Damit lässt sich die Ladung eines Öltröpfchens berechnen.

Anmerkung: Das Stokessche Gesetz mit η = 1,82·10^-5 kg/ms gilt bei derart kleinen Öltröpfchen (Der Radius der Öltröpfchen liegt in der Größenordnung von ca. 10^-6 – 10^-7 m) nicht mehr exakt, weil dies der Größenordnung der mittleren freien Weglänge der Luftmoleküle entspricht.

Durch diesen Fehler werden die Werte für die ermittelten Ladungsmengen etwas größer.

Methode 2: Sink- / Steigmethode

Bestimmung der Ladung durch Messen der Fallgeschwindigkeit und der Steiggeschwindigkeit unter Einfluss eines elektrischen Feldes (beide Richtungen) und der Spannung an der Millikankammer.

Vorgehensweise:

Die Spannung wird so hoch eingestellt, dass ein Öltröpfchen steigt. Diese Spannung wird dann umgekehrt (der Betrag bleibt gleich), wodurch das Öltröpfchen schneller sinkt als ohne elektrisches Feld.

Für das gleichförmige Sinken (unter Einfluss des elektrischen Feldes) gilt:

$F_ {el}+F_ {G}=F_ {R}$ und damit

$QE+mg=6\pi \eta r v_ {1}$ (a)

Dabei ist $v_{1}$ die Sinkgeschwindigkeit des Öltröpfchens im elektrischen Feld. Sie beträgt

$v_{1}=\dfrac {QE+mg}{6\pi \eta r}$

Für das gleichförmige Steigen (bei umgekehrter Spannung) gilt:

$F_ {el}-F_ {G}=F_ {R}$ und damit

$QE-mg=6\pi \eta r v_ {2}$ (b)

Dabei ist $v_{2}$ die Steiggeschwindigkeit des Öltröpfchens im elektrischen Feld. Sie beträgt

$v_{2}=\dfrac {QE-mg}{6\pi \eta r}$

Die Addition der beiden Gleichungen (a) und (b) ergibt:

$2QE=6\pi \eta r (v_ {1}+v_ {2})$ (1)

Mit Hilfe der Überlegungen in Methode 1 erhielt man für den Radius eines Öltröpfchens den Ausdruck

$r=\sqrt {\dfrac {9\eta v_{0}}{2\rho g}}$ mit $v_{0}$ Fallgeschwindigkeit ohne elektrisches Feld

Ersetzt man hier die Geschwindigkeit $v_{0}$ mit $v_ {0}=\dfrac {v_ {1}-v_ {2}}{2}$ (Begründung s.u.*), ergibt sich für den Radius

$r=\sqrt {\dfrac {9\eta (v_{1}-v_ {2})}{4\rho g}}=\dfrac {3}{2}\sqrt {\dfrac {\eta (v_{1}-v_ {2})}{\rho g}}$

* Begründung / Herleitung:

Subtrahiert man die Gleichungen (a) – (b), erhält man

$(QE+mg=6\pi \eta r v_ {1})-(QE-mg=6\pi \eta r v_ {2})$

und damit

$2mg=6\pi \eta r (v_ {1}-v_ {2})$

Ersetzt man die Masse durch $m=\rho V$ , erhält man

$2\cdot \dfrac {4}{3}\rho \pi r^{3}g=6\pi \eta r (v_ {1}-v_ {2})$ .

Kürzen und Umformen nach r liefert schließlich für den Radius

$r=\sqrt {\dfrac {9\eta (v_{1}-v_ {2})}{4\rho g}}$ (s.o.) bzw. mit $\sqrt {\dfrac {9}{4}}=\dfrac {3}{2}$

$r=\dfrac {3}{2}\sqrt {\dfrac {\eta (v_{1}-v_ {2})}{\rho g}}$

Setzt man nun diesen Ausdruck für $r$ in die Gleichung (1) ein, erhält man:

$2QE=6\pi \sqrt {\dfrac {9\eta \left( v_{1}-v_{2}\right) }{4\rho g}}\cdot \eta \left( v_{1}+v_{2}\right)$

Nun teilt man diese Gleichung durch $2E$ und ersetzt die elektrische Feldstärke mit $E=\dfrac {U}{d}$ .

Damit erhält man schließlich für die Ladung eines Öltröpfchens:

$Q=\dfrac {9}{2}\pi \sqrt {\dfrac {d^{2}\eta ^{3}}{\rho g}}\cdot \sqrt {v_{1}-v_{2}}\cdot \dfrac {v_{1}+v_ {2}}{U}$

oder anders geschrieben

$Q=\dfrac {9\pi d}{2U}\sqrt {\dfrac {\eta ^{3}}{\rho g}}\cdot \sqrt {v_{1}-v_{2}}\cdot \left( v_{1}+v_{2}\right)$

Sind nun die Größen η (Zähigkeit von Luft), ρ (Dichte des verwendeten Öls) und d (Plattenabstand) bekannt, lässt sich durch Messen der Steig- und Sinkgeschwindigkeit (v₁ und v₂) eines Öltröpfchens im elektrischen Feld, erzeugt durch die Spannung U, die Ladung eines Öltröpfchens berechnen.

Für die Auswertung des Versuchs muss auf diese Weise die Ladungsmenge für viele verschiedene Öltröpfchen bestimmt werden.

Ergebnis der Versuche

Wenn man den Versuch für eine sehr große Anzahl an Öltröpfchen wiederholt und die Ladung der einzelnen Öltröpfchen in einem Diagramm darstellt, stellt man fest, dass immer nur ganz bestimmte Beträge für die Ladung gemessen werden. Es gibt offenbar nur Öltröpfchen mit bestimmten Ladungen sowie einen kleinsten Wert für die gemessenen Ladungen. Alle anderen Ladungen sind Vielfache dieses kleinesten Wertes.

Das Ergebnis des Millikan-Versuchs lautet:

Alle ermittelten Ladungen sind das ganzzahlige Einfache oder Vielfache eines bestimmten Wertes.

Schlussfolgerung:

Dieser Wert entspricht der kleinsten existierenden Ladung, die sich nicht weiter teilen lässt.

Man sagt auch: Die Ladung ist gequantelt.

Die Elementarladung

Die kleinste existierende Ladung entspricht der Ladung eines Elektrons. Sie wird als Elementarladung e bezeichnet.

Die Elementarladung ist eine fundamentale Naturkonstante.

Der Literaturwert der Elementarladung beträgt:

e = 1,60217646 · 10^-19C

Ein Elektron hat die Ladung -e, ein Proton die Ladung e.

Info:

Um eine Ladungsmenge von $1C$ (ein Coulomb) zu erhalten, benötigt man $\frac {1C}{1,602\cdot 10^{-19}C}=6,24\cdot 10^{18}$ Elektronen bzw. Protonen!

Auch wenn ein Coulomb eine sehr große Ladungsmenge ist und in den meisten Versuchen Größenordnungen von einigen nC oder μC auftreten, hat man es in der Regel bei allen Versuchen mit einer sehr großen Anzahl an Elementarladungen zu tun, so dass die Quantelung der Ladung nicht bemerkbar ist.

weiter mit Elektronen im elektrischen Feld

zurück