Elektrisches Potential und elektrische Spannung

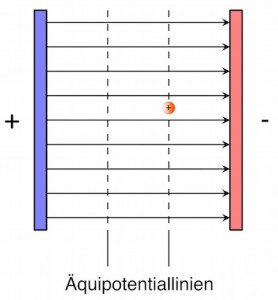
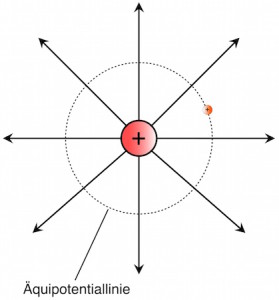
Potential und Spannung im elektrischen Feld

Befindet sich ein geladener Körper mit der Ladung in einem homogenen elektrischen Feld eines Plattenkondensators, so wirkt auf ihn an jedem Ort die konstante Kraft .

Durch diese Kraft kann er im homogenen Feld beschleunigt werden.

Dabei nimmt er die Energie  auf, wobei s die Strecke ist, über die er beschleunigt wurde.

Er besitzt anschließend somit die kinetische Energie .

Angenommen, der Körper sei positiv geladen und befindet sich in der Mitte des Kondensators – er kann dann über eine Strecke beschleunigt werden, die der Hälfte des Abstandes d entspricht.

Dabei kann er die Energie   bzw.  aufnehmen.

Mit anderen Worten:

Er hat das Potential, die Energie aufzunehmen.

Befindet er sich der Körper an der positiv geladenen Platte, kann er über die gesamte Strecke d beschleunigt werden. Er hat also das Potential, die Energie aufzunehmen.

Befindet er sich dagegen an der negativen Platte (Punkt P₀), kann er keine Energie mehr aufnehmen.

Der Energiebetrag, den der geladene Körper aufnehmen kann, hängt also vom Ort, von der Spannung U und seiner Ladung q ab.

So lässt sich für jeden Punkt des Feldes eine bestimmte Energie und damit ein bestimmer Wert für den Quotienten zuordnen.

Dieser Quotient wird als elektrisches Potential gegenüber dem Punkt P₀ bezeichnet und gibt an, welche Energie eine bestimmte Ladung q im Feld aufnehmen kann bzw. welche Energie man braucht, um diese Ladung von Punkt P₀ zu einem Punkt P_i zu bringen.

Beispiel:

In einem Plattenkondensator mit d = 10cm und U = 500V besteht zwischen beiden Platten eine Spannung (Potentialdifferenz, s.u.) von 500V. Zwischen der Mitte der Platten und einer Platte ist die Potentialdifferenz gerade halb so groß, sie beträgt also 250 V.

Die Potenzialdifferenz bzw. Spannung ist dabei unabhängig davon, welcher Bezugspunkt als Null-Potenzial gewählt wurde.

Linien oder Flächen gleichen Potenzials nennt man Äquipotenziallinien oder Äquipotenzialflächen. Sie stehen stets senkrecht zu den Feldlinien:

Beispielaufgabe:

Zwischen den beiden Platten eines Plattenkondensators liegt eine Spannung von U = 22,5V an. Der Abstand zwischen den Platten beträgt d = 3,0cm.

a) Wie groß ist die elektrische Feldstärke zwischen den Platten?

b) Ein positiv geladener Körper mit einer Ladung von Q = 6·10^–8C wird um 2,0cm parallel zu den Feldlinien verschoben. Wie groß ist die Änderung seiner potenziellen Energie?

c) Wie groß ist das Potenzial der positiv geladenen Platte, wenn man das der negativ geladenen Platte null setzt?

Analyse:

Beim elektrischen Feld eines Plattenkondensators handelt es sich um ein homogenes Feld. Es können die dafür geltenden Zusammenhänge angewendet werden.

Gesuchte Größen:

,     ,    

Gegebene Größen:

,     ,     ,    

Lösung:

a) Für die Feldstärke im homogenen elektrischen Feld gilt:

b) Die Änderung der Energie ist gleich der verrichteten Arbeit:

c) Das Potenzial ergibt sich aus Feldstärke und Plattenabstand:

Dies ist logisch, da die Potentialdifferenz der Spannung zwischen den Platten entsprechen muss.

Ergebnisse:

Die elektrische Feldstärke zwischen den Platten des Kondensators beträgt 750 V/m, die Änderung der potenziellen Energie bei Verschiebung eines Körpers im elektrischen Feld beträgt 9·10^–7J und das Potenzial der positiv geladenen Platte beträgt 22,5V.