Bestimmung der Wellenlänge von Licht mit dem Doppelspalt

Wellenlängenbestimmung von Licht mit dem Doppelspaltexperiment

Wir wollen nun mit Hilfe der angestellten Überlegungen und durch Messung benötigter Größen die Wellenlänge des Laserlichts bestimmen.

Dies ist mit einfachen geometrischen Überlegungen möglich:

Betrachten wir zunächst etwas genauer die beiden Teilstrahlen 1 und 2, die von jedem Spalt zu einem bestimmten Punkt auf dem Schirm gelangen und sich dort überlagern:

Bezeichnung der Größen:

g = Abstand der beiden Spalte

a = Abstand zwischen Doppelspalt und Schirm

M = Mittelpunkt des Beugungsbildes

d = Abstand zwischen Mitte (Hauptmaximum) und Punkt P

α = Winkel, unter dem Teilstrahlen den Spalt verlassen

Hinweis:

Da der Abstand zwischen Doppelspalt und Schirm a (einige Meter) um ein Vielfaches größer ist als der Abstand der beiden Spalte g (< 1mm), muss man für die Darstellung zwischen Doppelspalt und Schirm einen großen Bereich weglassen. Das ist durch die gestrichelten Linien angedeutet.

Im richtigen Maßstab müsste der Schirm bei dem hier verwendeten Spaltabstand einige hundert Meter weiter rechts stehen!

Die beiden Teilstrahlen sind praktisch parallel

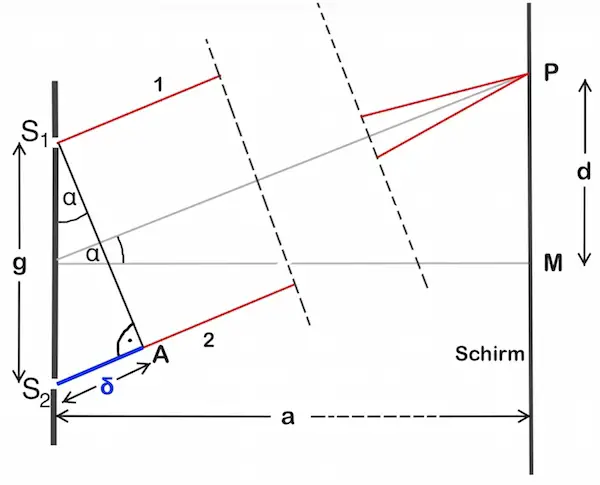
Man kann nun vereinfacht annehmen, dass beide Teilstrahlen ihren Spalt unter dem gleichen Winkel α verlassen und damit parallel zueinander verlaufen, obwohl sie letztendlich zum gleichen Punkt P auf dem Schirm gelangen.

Da a >> g, ist der Winkel α in Wirklichkeit extrem klein.

(Stelle Dir dazu den Punkt P auf gleicher Höhe aber 200m weiter rechts vor!)

Vom Gangunterschied zur Wellenlänge

In der Skizze erkennt man, dass Teilstrahl 2 einen längeren Weg zu Punkt P zurückzulegen hat als Teilstrahl 1. Diese Wegdifferenz Δs entspricht dem Gangunterschied δ (s. Skizze – blauer Abschnitt).

Liegt Punkt P genau beim Maximum erster Ordnung, so muss der Gangunterschied und damit die blaue Strecke gleich der Wellenlänge des Lichts sein.

Es gilt also δ = λ

Um diese Strecke zu ermitteln, stellt man folgende geometrische Überlegungen an:

In der Skizze findet man zwei Dreiecke:

Ein kleines Dreieck mit den Punkten S₁, S₂ und A und den Seitenlängen g, δ und der Strecke zwischen S₁ und A

Ein großes Dreieck mit den Punkten P, M und der Mitte von g und den Seitenlängen a, d und der gestrichelten Linie von der Mitte des Spaltes zu Punkt P.

Aus der Skizze ergeben sich für die beiden Dreiecke folgende Beziehungen:

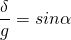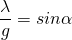Kleines Dreieck: $\dfrac {\delta}{g}=sin\alpha$ bzw. $\dfrac {\lambda}{g}=sin\alpha$ (es gilt ja δ = λ)

Großes Dreieck: 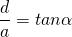$\dfrac {d}{a}=tan\alpha$

Da der Winkel α sehr klein ist (s.o.), gilt mit sehr guter Näherung:

$sin\alpha=tan\alpha$

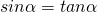
Damit lassen sich beide Gleichungen gleichsetzen, und man erhält den Zusammenhang

$\dfrac {\lambda}{g}=\dfrac {d}{a}$

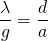
Stellt man diese Gleichung nach λ um, erhält man für die Wellenlänge

$\lambda=\dfrac {d\cdot g}{a}$

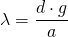
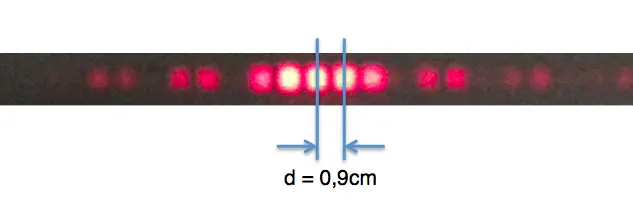
Ist der Spaltabstand g bekannt (dieser ist in der Regel auf dem Doppelspalt angegeben), lässt sich durch Messen des Abstandes a zwischen Schirm und Doppelspalt sowie des Abstandes d des Maximums erster Ordnung von der Mitte (Hauptmaximum) die Wellenlänge bestimmen.

Messwerte:

Die Maße der verwendeten Spalte ist auf der Spaltblende aufgedruckt.

Folgendes Bild zeigt die Spaltblende mit den verschiedenen Spalten (zum Vergrößern anklicken):

Verwendet wurde der Doppelspalt rechts oben. Der Spaltabstand beträgt also

g = 0,3mm

Der Abstand zwischen Doppelspalt und Schirm (Wand) wird mit einem Maßband gemessen.

Die Messung ergibt:

a = 4,23m

Anschließend wird bei verdunkeltem Raum der Abstand von der Mitte des Hauptmaximums bis zur Mitte eines Maximums erster Ordnung gemessen (Nur im Zentrum der Maxima ist genau die Bedingung δ = k · λ erfüllt).

Die Messung ergibt:

d = 0,9cm

Nun setzen wir diese Werte in die Formel für die Wellenlänge ein:

$\lambda=\dfrac {d\cdot g}{a}=\dfrac {0,009m\cdot 0,0003m}{4,23m}=6,38\cdot 10^{-7}m=638nm$

Ergebnis:

Aus dem Versuch ergibt sich die Wellenlänge des verwendeten Laserlichts zu λ = 638nm.

Damit bestätigt sich die Vermutung, dass die Wellenlänge von Licht vergleichsweise klein ist.

Die tatsächliche Wellenlänge, die auf dem Laser angegeben ist, beträgt 632,8nm.

Mit Hilfe des Doppelspaltversuchs konnte die Wellenlänge also mit einer hohen Genauigkeit ermittelt werden – die Abweichung von der tatsächlichen Wellenlänge liegt unter 1%!

Hinweis:

Der größte Fehler tritt beim Messen des Abstandes d zwischen Hauptmaximum und Maximum erster Ordnung auf, da die Maxima und Minima recht unscharf sind und die Intensität kontinuierlich zu- oder abnimmt.

Um die Messgenauigkeit zu vergrößern, hilft folgende Überlegung:

Maxima entstehen, wenn die Bedingung δ = k · λ erfüllt ist.

Für den Abstand des k-ten Maximums gilt demnach:

$\dfrac {k\lambda}{g}=\dfrac {d_{k}}{a}$ bzw. $d_{k}=k\cdot \dfrac {a\cdot \lambda}{g}$ ,

wobei d_k der Abstand zwischen dem Hauptmaximum und dem Maximum k-ter Ordnung ist.

Verdoppelt sich k, so verdoppelt sich auch der Abstand d.

Das bedeutet:

Die Abstände zweier benachbarter Maxima sind immer gleich groß, solange die Voraussetzung sinα = tanα erfüllt ist, also solange der Winkel α sehr klein ist.

Um den Abstand d zu ermitteln, ist es daher sinnvoll, den Abstand zweier Maxima höherer Ordnung zu messen und daraus den Abstand d zu berechnen. So minimiert man den Messfehler beim Messen von d.

Für das Minimum 1. Ordnung gilt:

$\delta=\dfrac {\lambda}{2}$

Für den Abstand der Minima erster Ordnung von der Mitte gilt also:

$d=\dfrac {a\cdot \lambda}{2g}$ .

Daraus ergibt sich:

Zwei benachbarte Maxima oder Minima haben jeweils den Abstand $\Delta d=\dfrac {a\cdot \lambda}{g}$

Mit Hilfe dieser Überlegungen kann man die Wellenlänge auch aus den Abständen zum k-ten Maximum berechnen:

$\lambda=\dfrac {d_{k}\cdot g}{k\cdot a}$

Frequenz des Lichts

Aus der Wellenlänge lässt sich nun auch die Frequenz f des Lichts berechnen.

Für alle Arten von Wellen gilt der Zusammenhang

$c=\lambda\cdot f$

Für die Frequenz gilt also

$f=\dfrac {c}{\lambda}$

Setzt man Wellenlänge und Lichtgeschwindigkeit ein, ergibt sich

$f=\dfrac {299792458\frac{m}{s}}{6,328\cdot 10^{-7}m}=4,74\cdot 10^{14}Hz$

Ergebnis:

Die Frequenz des Laserlichts beträgt f = 4,74 · 10¹⁴ Hz.

Hinweis:

Noch genauer lässt sich die Wellenlänge von Licht mit einem optischen Gitter mit kleiner Gitterkonstante bestimmen, da dann die Maxima wesentlich schärfer sind und ihr Abstand deutlich größer, was zu kleineren Messungenauigkeiten führt.

Erkenntnisse aus den Versuchen mit Einzel- und Doppelspalt

Licht wird beim Durchgang durch einen schmalen Spalt gebeugt.

Es entstehen für Wellen typische Interferenzerscheinungen.

Licht besitzt eine Wellenlänge von einigen 100 nm und eine Frequenz in der Größenordnung von 10¹⁴ Hz.

⇒ Es deutet also alles darauf hin, dass es sich bei Licht um eine elektromagnetische Welle handelt!

weiter mit Spektrum von Licht

zurück