Bragg-Reflexion

Röntgenbeugung an Kristallen

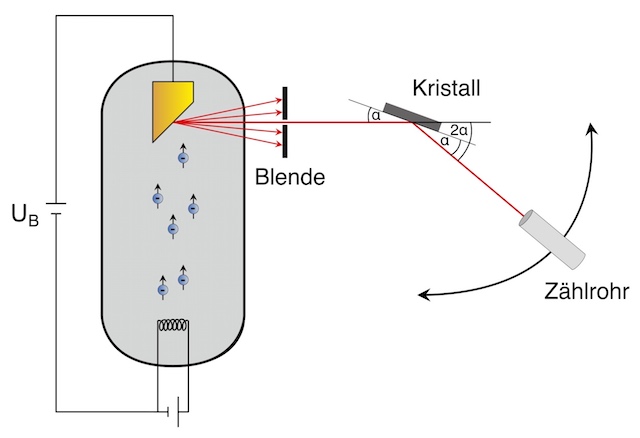
Nach der Idee von Max von Laue müssten mit Kristallen Interferenzerscheinungen von Röntgenstrahlung nachweisbar sein, da die innere Struktur von Kristallen ein Gitter mit sehr kleiner Gitterkonstanten darstellt.

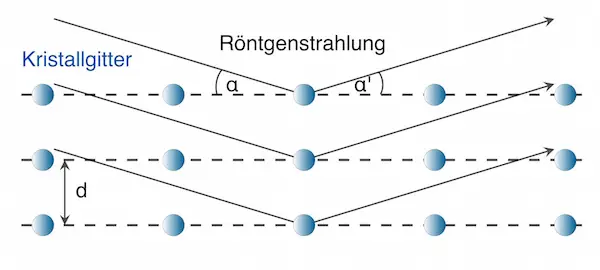
Durch die regelmäßige Anordnung der Atome im Kristallgitter werden die Röntgenstrahlen an verschiedenen Netzebenen reflektiert. Bei monochromatischer Röntgenstrahlung tritt bei der Überlagerung der reflektierten Strahlen Interferenz auf.

Die Teilstrahlen, die an den verschiedenen Netzebenen reflektiert werden, interferieren miteinander.

Durch die Vielzahl an Netzebenen mit dem konstanten Abstand d kommt es praktisch immer zur Auslöschung, wenn der Gangunterschied δ zwischen zwei benachbarten Teilstrahlen nicht genau einem ganzzahligen Vielfachen der Wellenlänge (also k · λ) beträgt – selbst bei kleinen Gangunterschieden (hier gleichbedeutend mit Wegunterschieden Δs) zwischen zwei benachbarten Teilstrahlen gibt es viele Netzebenen weiter einen Teilstrahl mit dem Gangunterschied λ/2.

Beispiel:

Beträgt der Gangunterschied zwischen dem ersten und zweiten Teilstrahl δ = 0,1λ, so gibt es zwischen dem 1. und 3. einen Gangunterschied von δ = 0,2λ, zwischen dem 1. und 4. wäre δ = 0,3λ, zwischen dem 1. und 5. wäre δ = 0,4λ, und zwischen dem 1. und 6. wäre die Bedingung für Auslöschung δ = 0,5λ erfüllt.

Das gleiche gilt für den 2. und 7., den 3. und 8. Teilstrahl usw.

(Die Erklärung ist praktisch die gleiche wie beim optischen Gitter!)

Der Glanzwinkel

Nur bei einem ganz bestimmten Winkel, nämlich wenn der Gangunterschied zweier benachbarter Teilstrahlen genau einem ganzzahligen Vielfachen der Wellenlänge entspricht, kommt es zur konstruktiven Interferenz.

Diesen Winkel bezeichnet man als Glanzwinkel.

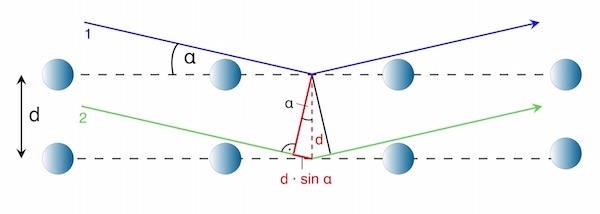
Der Wegunterschied Δs und damit der Glanzwinkel (dieser hängt von der Wellenlänge und vom Netzebenenabstand ab) ergibt sich aus einfachen geometrischen Überlegungen:

Aus der Skizze geht hervor:

Für den Zusammenhang zwischen dem Wegunterschied Δs zwischen Teilstrahl 1 und Teilstrahl 2 und dem Netzebenenabstand d gilt:

Mit Δs = k · λ (k = 1, 2, 3,…) erhält man die unten stehende Bragg-Gleichung. Sie wurde erstmals 1912 von William Lawrence Bragg entwickelt.

Die geometrischen Überlegungen sind ähnlich wie die bei der Interferenz an dünnen Schichten – nur dass hier keine Brechung auftritt (also n = 1) und es praktisch beliebig viele Schichten gibt.

Dadurch kommt es bei allen anderen Winkeln zur Auslöschung, denn durch die vielen Netzebenen ist für jeden Teilstrahl immer ein Partner zur Auslöschung vorhanden.

Mit Hilfe der o.g. Überlegungen ist es möglich,

• mit monochromatischer Röntgenstrahlung bekannter Wellenlänge den Netzebenenabstand von Kristallen zu bestimmen
• mit Hilfe von Kristallen mit bekanntem Netzebenenabstand die Wellenlänge bzw. das Spektrum von Röntgenstrahlung zu bestimmen

Die Drehkristallmethode

Eine Methode, mit der Röntgenspektren untersucht werden können, ist die sog. Drehkristallmethode.

Dabei wird ein Kristall mit Röntgenstrahlung bestrahlt. Die am Kristall reflektierte Röntgenstrahlung wird mit Hilfe eines Zählrohrs gemessen:

Kristall und Zählrohr werden gedreht, und die Intensität der reflektierten Strahlung wird in Abhängigkeit vom Streuwinkel gemessen.

Da für jeden Winkel eine andere Wellenlänge konstruktiv interferiert, kann man mit Hilfe der Bragg-Gleichung jedem Winkel eine Wellenlänge zuordnen. So lässt sich die Intensität in Abhängigkeit von der Wellenlänge darstellen.