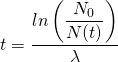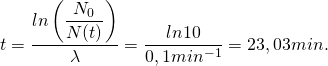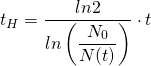Zerfallsgesetz und Halbwertszeit

Gesetze des radioaktiven Zerfalls

Beim radioaktiven Zerfall wandeln sich instabile Kerne in andere Kerne um.

Bei einem einzelnen instabilen Atomkern kann man allerdings nicht vorhersagen, wann er zerfallen wird – er kann in der nächsten Sekunde oder aber in Tausenden von Jahren zerfallen. Bei einer großen Anzahl von Atomkernen lässt sich aber eine statistische Aussage über den Ablauf des Zerfalls machen.

Für den Zerfall einzelner Kerne kann so eine Wahrscheinlichkeitsaussage gemacht werden. Die Zerfallswahrscheinlichkeit ist für jeden Kern eines Isotops gleich.

Der Zerfall einer großen Anzahl von Kernen gehorcht damit einem statistischen Zerfallsgesetz.

Die Halbwertszeit

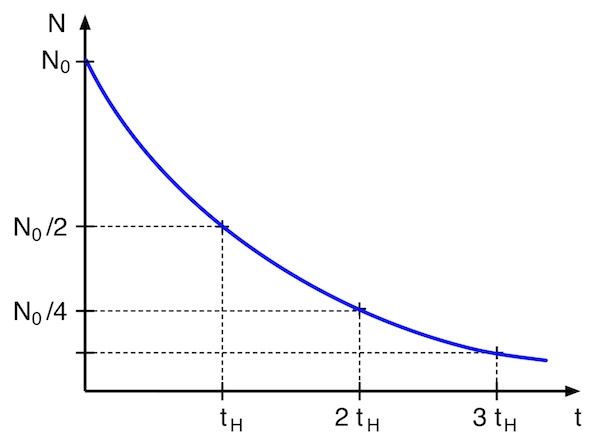
Beim radioaktiven Zerfall wird jeweils in einer bestimmten Zeit die Hälfte der Atome eines radioaktiven Stoffes umgewandelt.

Die Zeit, in der die Hälfte der vorhandenen Atomkerne zerfallen, bezeichnet man als Halbwertszeit $t_{H}$ .

Da die Zerfallswahrscheinlichkeit für jeden Kern eines Isotops gleich ist, hat jedes Nuklid eine charakteristische Halbwertszeit. Sie schwankt bei den verschiedenen Nukliden zwischen einigen Mikrosekunden und einigen Milliarden Jahren.

Trägt man die Anzahl der noch nicht zerfallenden Kerne N in Abhängigkeit von der Zeit t auf, so ergibt sich folgender Verlauf:

Die Halbwertszeit $t_{H}$ lässt sich aus dem Diagramm einfach ermitteln: Man schaut, nach welcher Zeit die Anzahl der ursprünglich vorhandenen Kerne N₀ auf die Hälfte abgenommen hat.

Nach zwei Halbwertszeiten ist die Anzahl auf 1/4 des Anfangswertes gesunken usw.

Mathematische Beschreibung des radioaktiven Zerfalls

Je mehr Kerne $N$ vorhanden sind, desto mehr Zerfälle pro Zeit finden statt.

Je mehr Zerfälle pro Zeit stattfinden, umso größer ist die zeitliche Änderung der Zahl der Ausgangskerne $N_{0}$ .

Die Anzahl der pro Zeiteinheit zerfallenden Kerne, also die Änderungsrate der Anzahl N $\dfrac {\Delta N}{\Delta t}$ bzw. $\dfrac {d N}{d t}$ ist proportional zur Anzahl der noch nicht zerfallenden Kerne $N$ .

Da die Anzahl der Kerne $N$ mit der Zeit abnimmt, ist die Änderungsrate $\Delta N=N_{2}-N_{1}$ negativ:

Damit gilt: $-\dfrac {dN}{dt}\sim N$ bzw. $-\dfrac {dN}{dt}=konst.\cdot N$

Diese Konstante ist eine für jedes Isotop charakteristische Konstante und heißt Zerfallskonstante $\lambda$ . Sie hat die Einheit $\frac {1}{s}$ bzw. $s^{-1}$ .

Die Gleichung $-\dfrac {dN}{dt}=\lambda N$

ist eine Differentialgleichung, die sich durch Integration oder mit dem Ansatz einer Exponentialfunktion lösen lässt.

Info: Wie löst man eine Differentialgleichung?

Lösen der Differentialgleichung bedeutet, eine Funktion $N(t)$ zu finden, die in die Differentialgleichung eingesetzt eine wahre Aussage ergibt. In diesem Fall muss man eine Funktion finden, deren Ableitung die gleiche Funktion mit einem konstanten negativen Faktor ergibt. Eine Funktion, bei der das der Fall ist, ist eine e-Funktion mit negativem Exponenten. (Eine solche Funktion kennen wir bereits von gedämpften Schwingungen.)

Für die Anzahl der nach einer bestimmten Zeit noch nicht zerfallenen Atomkerne ergibt sich so das Zerfallsgesetz:

Zerfallsgesetz

Für die Anzahl $N$ der nach einer bestimmten Zeit $t$ noch nicht zerfallenden (noch vorhandenen) Atomkerne gilt:

$\boldsymbol {N(t)=N_{0}\cdot e^{-\lambda\cdot t}}$

$N_{0}$ = Anfangszahl an Atomkernen zur Zeit t = 0

$\lambda$ = Zerfallskonstante

Berechnung der Zerfallskonstanten

Die Zerfallskonstante $\lambda$ lässt sich aus der Halbwertszeit berechnen:

Nach der Halbwertszeit $t_{H}$ sind noch die Hälfte der ursprünglichen Anzahl der Kerne $N_{0}$ vorhanden.

Es gilt also: $N(t_{H})=N_{0}\cdot e^{-\lambda \cdot t_{H}}=0,5\cdot N_{0}=\dfrac {1}{2}\cdot N_{0}$

Wir dividieren durch $N_{0}$ und erhalten

$\dfrac {N(t_{H})}{N_{0}}=e^{-\lambda \cdot t_{H}}=\dfrac {1}{2}$

Damit gilt $\dfrac {N(t_{H})}{N_{0}}=\dfrac {1}{2}$ bzw. für den Kehrwert $\dfrac {N_{0}}{N(t_{H})}=2$

Für die e-Funktion gilt (s.o.):

$e^{-\lambda \cdot t_{H}}=\dfrac {1}{2}$

Kehrt man das Vorzeichen im Exponenten um, so erhält man den Kehrwert:

$e^{\lambda \cdot t_{H}}=2$

Logarithmieren ergibt

$\lambda \cdot t_{H}=ln2$

Damit gilt für die Zerfallskonstante $\lambda=\dfrac {ln2}{t_{H}}$

und für die Halbwertszeit $t_{H}=\dfrac {ln2}{\lambda}$

So lassen sich also Zerfallskonstante und Halbwertszeit in Abhängigkeit voneinander ausdrücken.

Allgemein gilt für eine beliebige Zeit t das Zerfallsgesetz $N(t)=N_{0}\cdot e^{-\lambda\cdot t}$ .

Setzen wir die hergeleiteten Zusammenhänge ein, so ergibt sich für die Zerfallskonstante

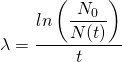$\lambda=\dfrac {ln\left(\dfrac {N_{0}}{N(t)}\right)}{t}$ und für die Zeit t $t=\dfrac {ln\left(\dfrac {N_{0}}{N(t)}\right)}{\lambda}$

Je nach Aufgabenstellung lassen sich so $t$ , $t_{H}$ , $\lambda$ , $N(t)$ oder $N_{0}$ berechnen:

Beispielaufgaben zum Zerfallsgesetz

Aufgabe 1

Bei einem radioaktiven Präparat sind ursprünglich 2,88 · 10²⁰ Atomkerne vorhanden.

Die Zerfallskonstante beträgt λ = 0,1 min^-1.

a) Wie groß ist die Anzahl der noch nicht zerfallenden Atomkerne nach einer Stunde?

gegeben: $N_{0}=2,88\cdot 10^{20}$ $\lambda =0,1min^{-1}$

Es gilt: $N(t)=N_{0}\cdot e^{-\lambda\cdot t}$

Das Produkt aus Zerfallskonstante und Zeit im Exponenten ergibt

$\lambda \cdot t=0,1\frac {1}{min}\cdot 60min=6$

Eingesetzt in das Zerfallsgesetz erhält man

$N(60min)=N_{0}\cdot e^{-6}=N_{0}\cdot 2,479 \cdot 10^{-3}=7,139 \cdot 10^{17}$

Antwort:

Nach einer Stunde sind noch 7,139 · 10¹⁷ Atomkerne vorhanden.

b) Berechne die Halbwertszeit!

Es gilt: $t_{H}=\dfrac {ln2}{\lambda}=6,93min.$

Antwort:

Die Halbwertszeit beträgt 6,93 Minuten.

c) Nach welcher Zeit sind 90% der ursprünglich vorhandenen Atomkerne zerfallen?

Vorüberlegung: Zu Beginn (bei t = 0) sind noch alle, also 100% der Kerne vorhanden. Nach der gesuchten Zeit sind 90% zerfallen, es sind also nur noch 10% der ursprünglichen Anzahl vorhanden.

Damit gilt: $N(t)=0,1\cdot N_{0}$ bzw. $\dfrac {N_{0}}{N(t)}=\dfrac {100}{10}=10$

Für die Zeit gilt (s.o.):

$t=\dfrac {ln\left(\dfrac {N_{0}}{N(t)}\right)}{\lambda}=\dfrac {ln10}{0,1min^{-1}}=23,03min.$

Antwort:

Nach 23,03 Minuten sind 90% der Atomkerne zerfallen.

Aufgabe 2

Radon zerfällt mit einer Halbwertszeit von 3,83 Tagen. Wie groß ist die Zerfallskonstante?

Wir verwenden den o.g. Zusammenhang zwischen Halbwertszeit und Zerfallskonstante:

$\lambda=\dfrac {ln2}{t_{H}}=\dfrac {ln2}{3,83d}=0,181d^{-1}$

Antwort:

Die Zerfallskonstante beträgt $\lambda =0,181d^{-1}$ .

Aufgabe 3

Ein radioaktives Gold-Präparat hat zum Zeitpunkt t = 0 eine Anzahl von 8,7 · 10¹³ noch nicht zerfallener Atomkerne. Nach einer Zeit von 24 Stunden ist die Anzahl der Atomkerne auf 2,7 · 10¹⁰ gesunken.

Wie groß ist die Halbwertszeit dieses Präparats?

gegeben: $N_{0}=8,7\cdot 10^{13}$ $N(t)=2,7\cdot 10^{10}$ mit $t=24h$