Relativistischer Impuls und relativistische Energie
Für die Ruheenergie eines Teilchens gilt:
![]() mit
mit ![]() = Ruhemasse
= Ruhemasse
Die Gesamtenergie eines bewegten Objektes ergibt sich aus der Summe der Ruheenergie und der kinetischen Energie:
![]() wobei
wobei ![]() hier die relativistische Masse
hier die relativistische Masse ![]() ist.
ist.
Für die relativistische kinetische Energie gilt
![]() bzw.
bzw. 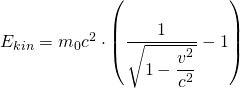
und damit für die relativistische Gesamtenergie
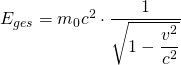 mit
mit ![]() (Ruheenergie, s.o.)
(Ruheenergie, s.o.)
Für den relativistischen Impuls gilt:
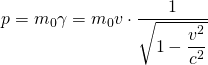
Beziehung zwischen Energie und Impuls:
Mit der Energie von Photonen ![]() und der De-Broglie-Beziehung
und der De-Broglie-Beziehung ![]() ergibt sich für den
ergibt sich für den
relativistischen Impuls für Photonen ![]() und damit für die Energie
und damit für die Energie ![]() .
.
Teilt man den relativistischen Impuls durch die relativistische (Gesamt-) Energie (s.o.), so erhält man
![]() und damit für die Geschwindigkeit
und damit für die Geschwindigkeit ![]() .
.
Damit lässt sich in der Formel für die relativistische Gesamtenergie die Geschwindigkeit ![]() ersetzen.
ersetzen.
So erhält man:
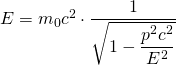 |
| ![]() Quadrieren führt zu
Quadrieren führt zu
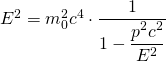 |
| ![]()
Durch Multiplikation mit dem Nenner auf der rechten Seite und dem Ausmultiplizieren der Klammer ergibt sich schließlich für die
Energie-Impuls-Beziehung:
![]() und für Elektronen
und für Elektronen ![]()
Damit gilt
![]() bzw.
bzw. ![]()
[ Die sog. Impuls-Energie beträgt ![]() . Diese ist invariant gegenüber einem Wechsel des Bezugssystems. ]
. Diese ist invariant gegenüber einem Wechsel des Bezugssystems. ]
De-Broglie-Wellenlänge für Elektronen hoher kinetischer Energie (relativistisch)
Wir verwenden nun die Beziehung für relativistische Energie und Impuls zur Herleitung der De-Broglie-Wellenlänge für Elektronen hoher Energie.
Mit ![]() folgt für den Impuls
folgt für den Impuls
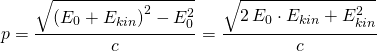
Diesen setzen wir nun in die De-Broglie-Beziehung ![]() ein und erhalten so:
ein und erhalten so:
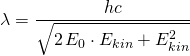
Schließlich ersetzen wir die Energien mit ![]() und
und ![]() und erhalten für die
und erhalten für die
De-Broglie-Wellenlänge (relativistisch):
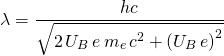
Zur Erinnerung: Die klassische Berechnung ergab für die De-Broglie-Wellenlänge
![]() (klassisch)
(klassisch)
Für hohe Beschleunigungsspannungen müssen wir also auch die De-Broglie-Wellenlänge relativistisch berechnen.
Der Fehler, den man mit der klassischen Berechnung macht, ist bei Beschleunigungsspannungen von einigen kV vernachlässigbar. Er beträgt bei 1 kV nur etwa 0,05%, bei 10 kV knapp 0,5%. Für UB = 100 kV liegt der Fehler bei 4,8%, bei 1 MV sind es knapp 41%.