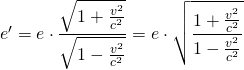Minkowski-Diagramme
Im Jahre 1908 führte Hermann Minkowski spezielle Weg-Zeit-Diagramme ein, mit der sich alle Effekte der speziellen Relativitätstheorie verständlich darstellen lassen. Sowohl die Zeitdilatation als auch die Längenkontraktion lassen sich darin zeichnerisch darstellen und ermitteln. In diesen Minkowski-Diagrammen ist es üblich, die Zeit t auf der senkrechten und die Strecke x auf der waagerechten Achse aufzutragen.
In Minkowski-Diagrammen werden Ereignisse als Punkt mit den Koordinaten (x, t) dargestellt. Die Menge aller Ereignisse bildet eine Weltlinie.
Jeder Punkt auf der Weltlinie entspricht einem bestimmten Ort x zu einem bestimmten Zeitpunkt t. Ein solcher Punkt wird Weltpunkt genannt.
Da die Effekte der Relativitätstheorie nur bei sehr hohen Geschwindigkeiten nachweisbar sind, hat man es mit großen Geschwindigkeiten und entsprechend großen Weglängen zu tun. Die Skalierung der Achsen wird daher folgendermaßen vorgenommen:
Skalierung der t-Achse: Sekunden (s)
Skalierung der x-Achse: Lichtsekunden (Ls)
Die Achseneinteilung wird dabei so vorgenommen, dass gleiche Strecken für eine Sekunde und eine Lichtsekunde gewählt werden, also beispielsweise: Ein Zentimeter auf der t-Achse entspricht einer Sekunde, ein Zentimeter auf der x-Achse entspricht einer Lichtsekunde.
Daraus ergibt sich:
Die Weltlinie eines Lichtsignals hat die Steigung 1 bzw. 45°. Flachere Weltlinien können nicht existieren, da nichts schneller sein kann als das Licht.
Im folgenden Minkowski-Diagramm sind neben der Weltlinie eines Lichtsignals W1 drei weitere Weltlinien dargestellt, die anschließend erläutert werden:
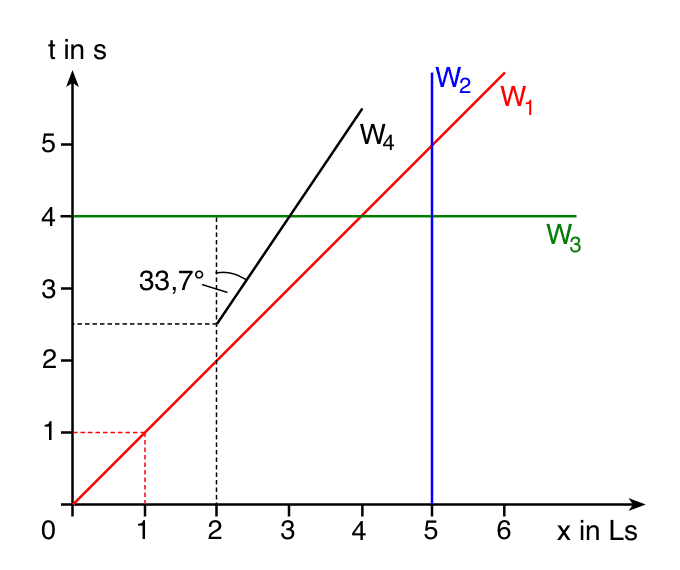
Erläuterung der Weltlinien:
| W1 |
Weltlinie eines Lichtsignals |
| W2 |
Weltlinie von Ereignissen am gleichen Ort (ortsgleiche Ereignisse) |
| W3 |
Weltlinie von Ereignissen zur gleichen Zeit (zeitgleiche Ereignisse) |
| W4 |
Weltlinie eines Körpers, der sich mit 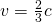 in positive x-Richtung bewegt. Er startet bei in positive x-Richtung bewegt. Er startet bei 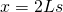 und und 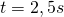 . . |
Der Winkel zwischen der t-Achse und der Weltlinie W4 ist von der Geschwindigkeit des Körpers abhängig. Es gilt:
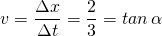 Damit ergibt sich für dieses Beispiel ein Winkel von
Damit ergibt sich für dieses Beispiel ein Winkel von 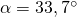 (s. Skizze)
(s. Skizze)
In unserem Koordinatensystem für das Inertialsystem S ist der Körper, zu dem die Weltlinie W4 gehört, in Bewegung, während sich der Beobachter in S in Ruhe befindet. Wir wollen nun das Koordinatensystem für das Inertialsystem S‘ zeichnen, in dem der Körper ruht.
Für dieses Koordinatensystem muss gelten:
- Die t‘-Achse muss parallel zur Weltlinie W4 sein (dann ist x‘ = konst.).
- Für den Winkel zwischen t- und t‘-Achse gilt wie für W4:
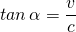
- Die x‘-Achse muss symmetrisch zu W1 liegen (c ist in allen Inertialsystemen gleich).
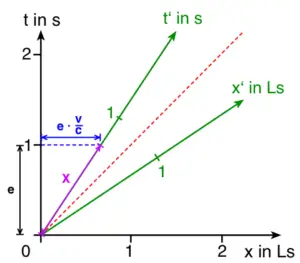
Das folgende Minkowski-Diagramm enthält nun neben den Weltlinien W1 (Lichtsignal) und W4 die so konstruierten Achsen t‘ und x‘. Es ergibt sich statt eines rechtwinkligen Koordinatensystems ein spitzwinkliges Koordinatensystem (für negative Geschwindigkeiten, also für Ausbreitung in negative x-Richtung ergibt sich ein stumpfwinkliges Koordinatensystem):
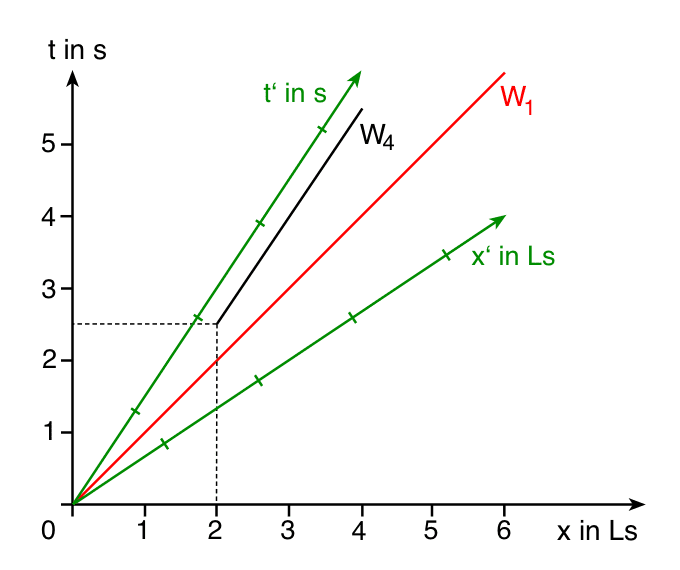
Wichtig ist nun folgendes:
Die Längeneinheiten für die Achseneinteilungen unterscheiden sich zwischen S und S‘. Wenn wir für eine Sekunde bzw. eine Lichtsekunde in S einen Zentimeter gewählt haben, beträgt die Länge für eine Sekunde bzw. eine Lichtsekunde in S‘ nicht auch ein Zentimeter.
Zwischen den Längeneinheiten der Achseneinteilungen e für S und e‘ für S‘ gilt folgende Beziehung:
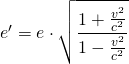 bzw.
bzw. 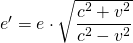
Für unsere Beispiel mit 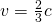 und
und 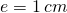 ergibt sich so
ergibt sich so
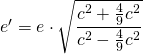 =
= 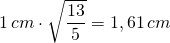
Die Herleitung der Beziehung zwischen e und e‘ findest Du weiter unten.
Die Achsenskalierung für das spitzwinklige Koordinatensystem wurde in der vorherigen Skizze bereits entsprechend vorgenommen.
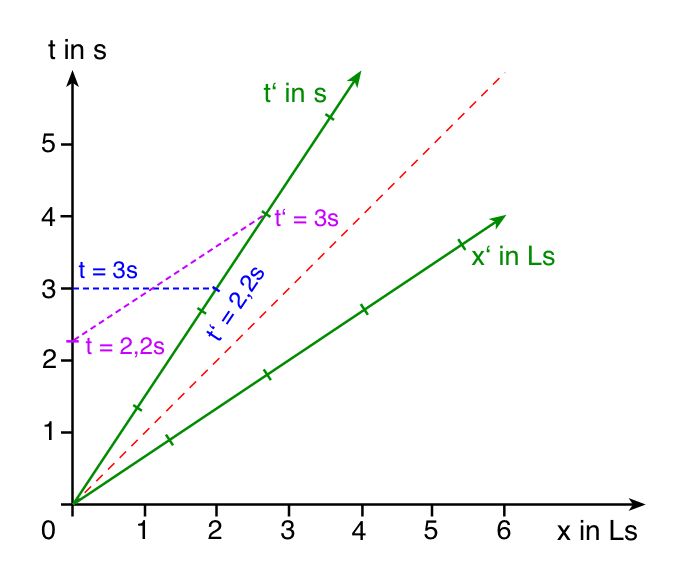
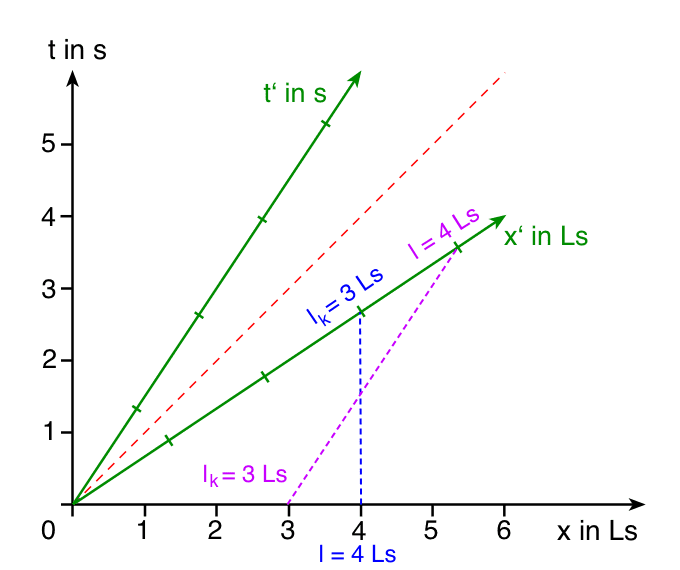
Nun lassen sich für jedes Ereignis Zeit- und Ortskoordinaten für das jeweilige Bezugssystem bestimmen. Außerdem lassen sich die unterschiedlichen Zeiten und Längen, die in verschiedenen Inertialsystemen gemessen werden, konstruieren.


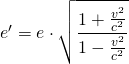 bzw.
bzw. 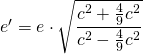 =
=