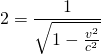Die Relativität der Masse
Wir haben gesehen, dass zwei Grundgrößen der Mechanik – die Länge und die Zeit – aufgrund ihrer Relativität modifiziert werden müssen. Daher ist zu erwarten, dass auch andere Größen, wie Impuls, Energie und Masse, modifiziert werden müssen.
Es lässt sich zeigen, dass der Impulserhaltungssatz auch im relativistischen Bereich seine Gültigkeit behält.
Für den relativistischen Impuls lässt sich herleiten, dass dieser definiert werden muss als
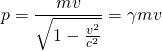 . relativistischer Impuls
. relativistischer Impuls
Relativistische Massenzunahme
Die o.g. relativistische Definition des Impulses wird oft als relativistische (oder auch dynamische) Massenzunahme eines Körpers interpretiert. Damit ließe sich die klassische Form des Impulses beibehalten:
![]() mit
mit ![]() als relativistische Masse
als relativistische Masse
Für die relativistische Masse, die dann mit der Geschwindigkeit wachsen muss, gilt:
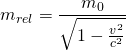 bzw.
bzw. ![]()
Dabei wird ![]() als Ruhemasse eines Körpers bezeichnet. Das ist die Masse, die der Körper in einem Bezugssystem besitzt, in dem er sich in Ruhe befindet. Bewegt sich der Körper innerhalb eines Bezugssystems mit der Geschwindigkeit
als Ruhemasse eines Körpers bezeichnet. Das ist die Masse, die der Körper in einem Bezugssystem besitzt, in dem er sich in Ruhe befindet. Bewegt sich der Körper innerhalb eines Bezugssystems mit der Geschwindigkeit ![]() , so misst man in diesem Bezugssystem die (größere) relativistische Masse
, so misst man in diesem Bezugssystem die (größere) relativistische Masse ![]() . Die Masse des Körpers scheint sich also mit der Geschwindigkeit zu erhöhen.
. Die Masse des Körpers scheint sich also mit der Geschwindigkeit zu erhöhen.
Ein Gedankenexperiment verdeutlicht die aus der Impulserhaltung (s.o.) resultierende Massenzunahme:
Ein Meteorit, der auf der Erde einschlägt, erzeugt beim Einschlag einen Schaden, der vom Impuls – also von der Masse und der Geschwindigkeit – des Meteoriten abhängt.
Beobachtet man den Einschlag von einem sich mit hoher Geschwindigkeit senkrecht zur Meteoritenbahn bewegenden Raumschiff, so wird von dort aus die gleiche Strecke des Meteoriten bis zur Erde gemessen, da die Längenkontraktion nur in Bewegungsrichtung auftritt. Vom Raumschiff aus wird aufgrund der Zeitdilatation jedoch eine größere Zeitspanne bis zum Einschlag gemessen, was zu einer kleineren gemessenen Geschwindigkeit führt.
Der Beobachter im Raumschiff sieht also den Meteoriten mit einer kleineren Geschwindigkeit auf der Erde einschlagen – er sieht jedoch die gleiche Zerstörung, denn diese kann nicht vom Beobachter abhängen. Wenn der Impuls also gleich bleibt, dann muss bei geringerer Geschwindigkeit die Masse des Meteoriten aus Sicht des Raumschiffs zugenommen haben.
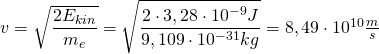 ,
,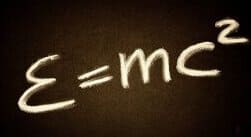
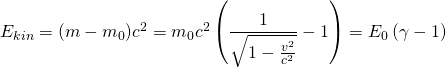
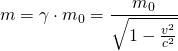
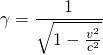
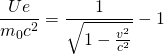
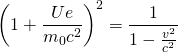
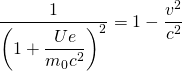
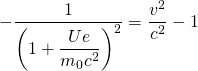
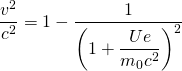
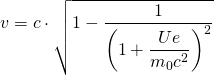
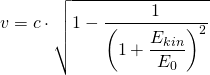
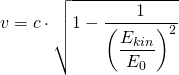 bzw.
bzw. 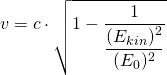
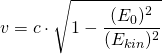 bzw.
bzw. 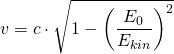
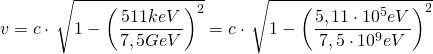
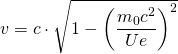 bzw.
bzw.