Stehende Wellen

Reflexion von Wellen und stehende Wellen

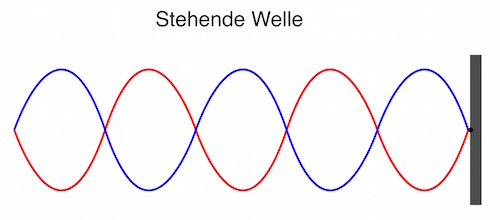
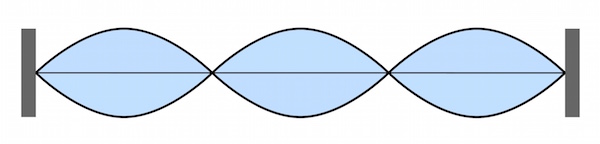
Ein besonderes Phänomen entsteht, wenn sich zwei Wellen gleicher Frequenz und Amplitude überlagern, die sich in entgegengesetzte Richtung ausbreiten.

Am häufigsten tritt dieses Phänomen auf, wenn eine Welle reflektiert wird und sich so mit ihrer eigenen Reflexion überlagert.

Reflexion linearer Wellen

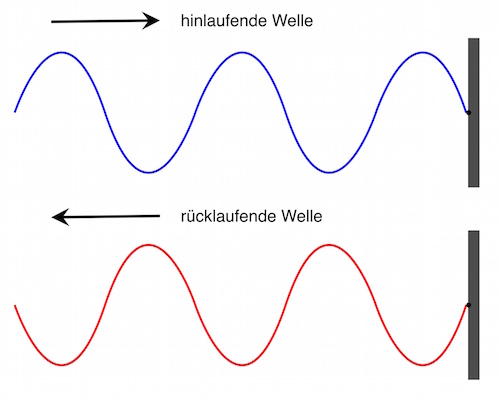
Die Reflexion einer linearen Welle lässt sich mit einem Seil oder einer langen Feder untersuchen. Dazu wird eine lange Feder an einem Gegenstand befestigt (oder festgehalten) und am anderen Ende eine Störung erzeugt, indem die Feder einmal schnell ausgelenkt wird.

Beobachtung:

Bei der Reflexion wird die Richtung der Auslenkung umgekehrt – aus einem Wellenberg wird ein Wellental und umgekehrt.

Man sagt, es tritt ein Phasensprung um 180° oder bzw. einer halben Wellenlänge auf.

Man bezeichnet eine solche Reflexion als Reflexion am festen Ende (da das gegenüberliegende Ende festgehalten wird).

Befestigt man das Ende der Feder nicht an einem festen Gegenstand, sondern an einem Faden, so dass das Ende der Feder frei ausschwingen kann, so tritt kein Phasensprung auf.

Bei einer solchen Reflexion spricht man von einer Reflexion am losen (oder freien) Ende.

Stehende Wellen

Erzeugt man in der Feder kontinuierlich und gleichmäßig Schwingungen, die sich als Welle innerhalb der Feder ausbreiten, überlagert sich die hinlaufende Welle mit der reflektierten Welle. Dabei addieren sich, wie im Abschnitt Interferenz beschrieben, die Auslenkungen an jedem Punkt.

Bei bestimmten Frequenzen kommt es dabei zu stehenden Wellen:

Es bilden sich Bereiche, in denen die Auslenkung maximal schwankt (Schwingungsbäuche) und Bereiche, in denen die Auslenkung ständig Null ist (Schwingungsknoten).

Da sich die Knoten und Bäuche nicht bewegen, sondern immer an der gleichen Stelle bleiben, spricht man von stehenden Wellen.

Benachbarte Knoten haben einen Abstand von einer halben Wellenlänge (λ/2).

Voraussetzung für die Entstehung stehender Wellen

Stehende Wellen entstehen nur bei bestimmten Frequenzen. Diese hängen von der Länge des Systems (in diesem Beispiel von der Länge der Feder) ab.

Bei Schwingungszuständen, in denen sich stehende Wellen bilden, spricht man von Eigenschwingungen des Systems.

Die einfachste Form entsteht bei der kleinsten Frequenz und heißt Grundschwingung. Die Eigenschwingungen, die bei höheren Frequenzen entstehen, nennt man Oberschwingungen.

Damit eine stehende Welle entsteht, muss eine bestimmte Anzahl an Wellenlängen (bzw. Bruchteilen einer Wellenlänge) auf die Länge des Systems passen.

Je nach Bedingung (festes oder loses Ende), ergeben sich so die möglichen Eigenschwingungen.

Eigenschwingungen eines Wellenträgers mit zwei festen Enden

Die folgenden Abbildungen zeigen die Bedingungen für das Entstehen einer stehenden Welle bei zwei festen Enden. Der Abstand der beiden festen Enden entspricht der Länge des Systems:

Grundschwingung        Es gilt:  

           

1. Oberschwingung        Es gilt:  

           

2. Oberschwingung        Es gilt:  

           

Allgemein gilt: Die Bedingung für stehende Wellen bei zwei festen Enden lautet:

n. Oberschwingung:                  mit 

Die gleichen Bedingungen gelten auch bei zwei freien Enden.

Eigenschwingungen eines Wellenträgers mit einem festen und einem freien Ende

Für ein festes und ein freies Ende ergeben sich folgende Bedingungen:

Grundschwingung:        

1. Oberschwingung:      

2. Oberschwingung:      

n. Oberschwingung:                mit 

Allgemein lassen sich die Bedingungen folgendermaßen zusammenfassen: