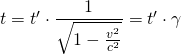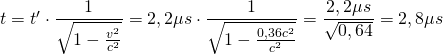Häufig wird der oben beschriebene Sachverhalt einfach ausgedrückt mit dem Satz:
„Bewegte Uhren gehen langsamer.“
Etwas genauer müsste man sagen:
Relativ zu einem Beobachter bewegte Uhren laufen für diesen Beobachter langsamer (als Uhren, die sich im Vergleich dazu in Ruhe befinden).
Denn wie wir schon bei der Relativität der Gleichzeitigkeit gesehen haben, kann man nicht entscheiden, welches System in Ruhe ist und welches sich bewegt. Das bedeutet, dass jeder Beobachter einen Vorgang in einem anderen relativ dazu bewegten System langsamer ablaufen sieht. Beide Ansichten sind völlig gleichberechtigt, und jeder misst in seinem Bezugssystem die für ihn richtige Zeit.
Diese in seinem Ruhesystem gemessene Zeit ist jeweils die kürzeste gemessene Zeit für einen Vorgang und wird als Eigenzeit bezeichnet.
In einem anderen dazu bewegten System aus wird die Zeitdauer für den gleichen Vorgang größer gemessen.
Ist die Zeitdilatation real?
Das Konzept der Zeitdilatation ist für uns schwer begreifbar, weil es unser Verständnis der Zeit als absolute Größe verletzt.
Wie wir bei der Berechnung des Lorentzfaktors gesehen haben, ist der Effekt der Zeitdilatation vernachlässigbar, wenn die Geschwindigkeiten nicht in der Nähe der Lichtgeschwindigkeit sind. Daher ist er in unserem Alltag nicht bemerkbar, denn im Alltag sind alle Geschwindigkeiten viel kleiner als  . Tatsächlich handelt es sich jedoch eine Erscheinung, die real ist und auch nichts mit der Art der Zeitmessung zu tun hat.
. Tatsächlich handelt es sich jedoch eine Erscheinung, die real ist und auch nichts mit der Art der Zeitmessung zu tun hat.
Experimente, in denen Atomuhren in Flugzeugen um die Erde geschickt wurden, haben bereits Anfang der 1970er-Jahre die Vorhersagen und damit die o.g. Gleichung bestätigt.
Bereits früher gab es Experimente mit Elementarteilchen, die man fast auf Lichtgeschwindigkeit beschleunigen konnte, mit denen die Zeitdilatation bestätigt wurde. Einige dieser Elementarteilchen, wie z.B. Myonen, sind äußerst instabil und zerfallen nach kurzer Zeit bereits wieder.
Lebensdauer von bewegten Myonen bestätigen die Zeitdilatation
Myonen sind Teilchen mit geringer Masse, die sich mit vergleichsweise geringer Energie auf Geschwindigkeiten nahe der Lichtgeschwindigkeit beschleunigen lassen.
Die mittlere Lebensdauer von Myonen beträgt in Ruhe nur 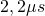 .
.
Aufwändige Experimente mit Myonen haben gezeigt, dass Myonen, die sich mit hoher Geschwindigkeit bewegen, eine längere Lebensdauer haben, und zwar um genau den Betrag, der mit der Zeitdilatation vorhergesagt werden kann.
Beispielaufgabe
a) Welche mittlere Lebensdauer hat ein Myon, welches sich mit 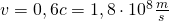 (
(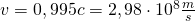 ) relativ zum Labor, in dem die Zeitmessung stattfindet, bewegt?
) relativ zum Labor, in dem die Zeitmessung stattfindet, bewegt?
b) Welche Entfernung legt es zurück, bevor es zerfällt?
Lösung
a) Im Bezugssystem S‘ des Myons besitzt das Myon eine Lebensdauer von 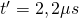 . Für einen Beobachter im Labor (System S) lebt das Myon aufgrund der Zeitdilatation länger, die im Labor gemessene Zeit
. Für einen Beobachter im Labor (System S) lebt das Myon aufgrund der Zeitdilatation länger, die im Labor gemessene Zeit 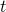 ist also größer als
ist also größer als 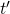 .
.
Mit der Geschwindigkeit 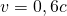 des Myons gegenüber dem Beobachter erhält man mit der Gleichung für die Zeitdilatation für die Lebensdauer
des Myons gegenüber dem Beobachter erhält man mit der Gleichung für die Zeitdilatation für die Lebensdauer 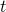 im Labor:
im Labor:
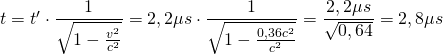
Mit 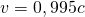 erhält man:
erhält man:
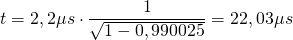
b) Nach der klassischen Physik lässt sich die Entfernung aus Geschwindigkeit und Lebensdauer berechnen.
Für den zurückgelegten Weg  gilt:
gilt:
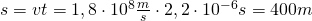 (In der klassischen Physik gilt:
(In der klassischen Physik gilt:  .)
.)
Die Relativitätstheorie sagt jedoch die längere Strecke
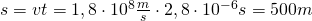 (für
(für 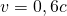 ) bzw.
) bzw.
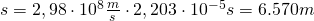 (für
(für 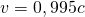 )
)
voraus.
Im Experiment wird tatsächlich diese längere von der Relativitätstheorie vorhergesagte Strecke gemessen.
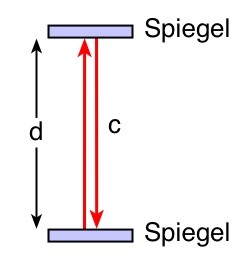
![]() bewegen. Die Laufzeit des Lichts ist damit ein Maß für die Zeitdauer.
bewegen. Die Laufzeit des Lichts ist damit ein Maß für die Zeitdauer.![]() .
.![]() .
.![]() , so beträgt die Laufzeit des Lichts bis zum anderen Spiegel
, so beträgt die Laufzeit des Lichts bis zum anderen Spiegel ![]() .
.
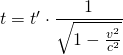
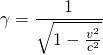 .
.