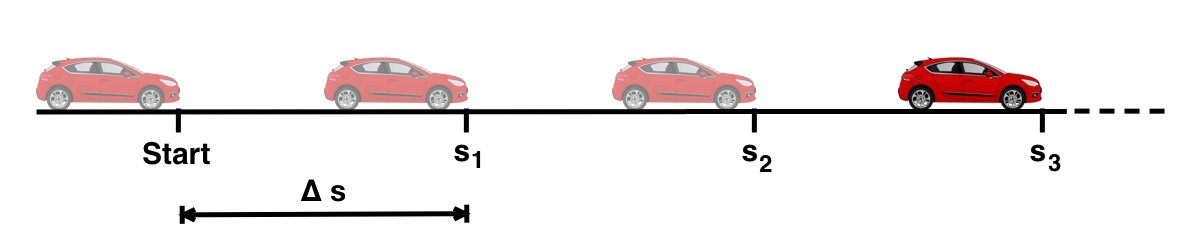
Aus den Messwerten lässt sich bereits erkennen, dass die Differenzen der Zeiten etwa gleich groß sind. Das bedeutet, dass das Auto für jeden Teilabschnitt von 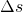 = 10 m etwa die gleiche Zeit benötigt hat. Das Auto scheint also weder schneller noch langsamer geworden zu sein. Abweichungen davon könnten aufgrund von Messungenauigkeiten (s.o.) entstanden sein.
= 10 m etwa die gleiche Zeit benötigt hat. Das Auto scheint also weder schneller noch langsamer geworden zu sein. Abweichungen davon könnten aufgrund von Messungenauigkeiten (s.o.) entstanden sein.
Um das besser beurteilen zu können und um die gesamte Bewegung auf einen Blick zu erfassen, ist es sinnvoll und üblich, die Messwerte grafisch in Form eines Diagramms darzustellen.
Wie man das macht und was es dabei zu beachten gibt, erfährst Du im nächsten Abschnitt!
Grafische Darstellung von Messwerten
Für die grafische Darstellung von Messwerten werden diese in einem Koordinatensystem gegeneinander aufgetragen.
Wir zeichnen also ein Koordinatensystem, in dem wir auf die waagerechte Achse (auch Abszisse genannt) die Zeit t und auf die senkrechte Achse (Ordinate) die zurückgelegte Strecke s auftragen.
Für das Anfertigen eines Diagramms gibt es bestimmte Regeln und Vorgehensweisen, die Du unbedingt beachten solltest. Diese findest Du auf der folgenden Seite:
Regeln für das Erstellen eines Diagramms
Das Diagramm könnte in Deinem Heft wie folgt aussehen:
Zurückgelegte Strecke s eines Autos in Abhängigkeit von der Zeit t
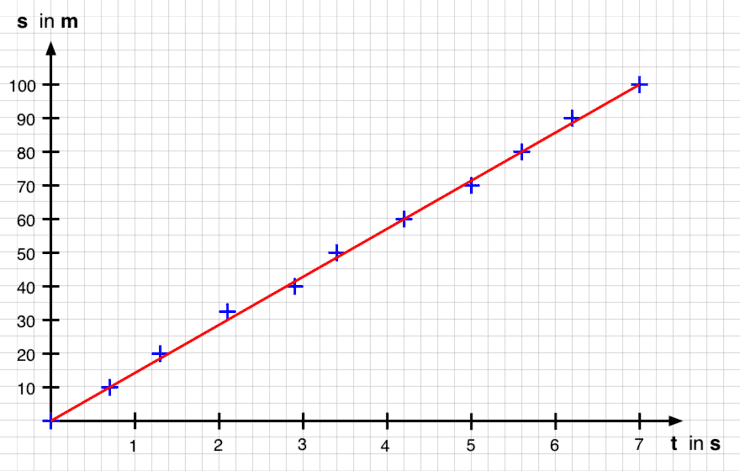
Zeit-Weg-Diagramm
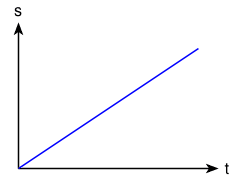
Wie Du siehst, ergibt sich ein linearer Verlauf, es lässt sich also eine Gerade zeichnen.
Beachte dabei, dass wir auch einen Messpunkt in den Ursprung gelegt haben. Da wir zu Beginn festgelegt haben, dass die Uhren gestartet werden, wenn das Auto genau beim Startpunkt ist, gilt hier: s = 0 und t = 0. Dieser Punkt ist damit also sicher!
Ausgleichsgerade
Auch wenn die eingezeichneten Messpunkte nicht genau auf dieser Geraden liegen, gehen wir von einem linearen Verlauf aus – wie schon oben diskutiert, müssen wir bei jeder Messung davon ausgehen, dass sie ein wenig fehlerhaft ist – vermutlich haben wir mal zu lange und mal zu kurze Zeiten gemessen. Das versuchen wir mit der Geraden auszugleichen. Man nennt eine solche Gerade daher Ausgleichsgerade.
Eine Ausgleichsgerade wird so gezeichnet, dass sie den Verlauf möglichst genau beschreibt, wobei sie allen Punkten möglichst nahe sein sollte, was meist der Fall ist, wenn etwa gleich viele Messpunkte oberhalb wie unterhalb der Ausgleichsgeraden liegen. Da der Ursprung festgelegt wurde (s.o.), was meistens der Fall ist, muss auch die Ausgleichsgerade durch den Ursprung verlaufen.
Das Zeit-Weg-Diagramm
Wir haben im obigen Diagramm den Weg und die Zeit gegeneinander aufgetragen. Man nennt ein solches Diagramm Zeit-Weg-Diagramm. Üblich (und vor allem früher benutzt) ist auch die Bezeichnung Weg-Zeit-Diagramm.
Was kann man mit dem Zeit-Weg-Diagramm anfangen?
Ergibt sich im Zeit-Weg-Diagramm eine Gerade, so lassen sich folgende Aussagen machen:
- Die zurückgelegte Wegstrecke s und die dafür benötigte Zeit t sind zueinander proportional. In Kurzschreibweise:
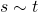
- In gleich langen Zeitabschnitten werden gleich lange Wege zurückgelegt.
- Die Geschwindigkeit ist konstant.
Eine solche Bewegung bezeichnet man als gleichförmige Bewegung.
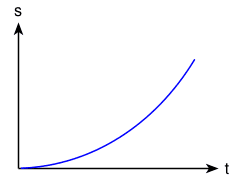
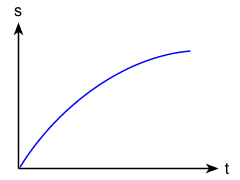
Ist die Bewegung nicht gleichförmig, sondern wird das Objekt langsamer oder schneller, ergibt sich im Zeit-Weg-Diagramm keine Gerade, sondern eine Kurve. Man kann aus einem Zeit-Weg-Diagramm auch ohne Skalierung auf einen Blick sofort erkennen, ob eine Bewegung gleichförmig ist oder nicht und ob die Geschwindigkeit größer oder kleiner wird:
 Beispiele: Eisenbahnzug, Anheben einer Last, rollende Bowlingkugel, fallender Stein
Beispiele: Eisenbahnzug, Anheben einer Last, rollende Bowlingkugel, fallender Stein Beispiele: Pendel einer Uhr, Glocke, Schaukel, Gitarrensaite
Beispiele: Pendel einer Uhr, Glocke, Schaukel, Gitarrensaite Beispiele: Zeiger einer Uhr, Rad eines Autos, Ventilator, Karussell
Beispiele: Zeiger einer Uhr, Rad eines Autos, Ventilator, Karussell