Wir haben am Ende des vorherigen Abschnitts die Eigenschaft der Bewegung des Autos erfasst und erkannt, dass es sich um eine gleichförmige Bewegung handelt.
In der folgenden Übersicht wird noch einmal zusammengefasst, was eine gleichförmige Bewegung ausmacht:
Bei einer gleichförmigen Bewegung bleibt also die Geschwindigkeit gleich – das heißt, das Objekt bewegt sich immer gleich schnell.
Im nächsten Abschnitt wollen wir überlegen, wie die Größe Geschwindigkeit definiert ist und wie wir sie ermitteln können.
Hinweis:
Bei genauer Messung würde man bei praktisch jeder Bewegung aus dem Alltag feststellen, dass die Geschwindigkeit nicht exakt gleich bleibt. Wir können kleine Geschwindigkeitsänderungen jedoch vernachlässigen und so tun, als würde die Geschwindigkeit sich nicht ändern. Das macht es uns einfacher, und wir machen nur einen kleinen Fehler.
Die Vernachlässigung kleiner Abweichungen von der Realität macht es uns überhaupt erst möglich, Gesetzmäßigkeiten zu finden, anzuwenden und damit Vorhersagen zu treffen. Das wird Dir im Physikunterricht immer wieder begegnen.
Sicher kennst Du den Begriff “Geschwindigkeit” bereits aus dem Alltag und weißt, was man darunter versteht und in welcher Einheit die Geschwindigkeit angegeben wird.
Vermutlich ist Dir auch die Einheit “Kilometer pro Stunde” oder kurz “km/h” geläufig. Häufig hört man auch den Begriff “Stundenkilometer”, was das gleiche meint aber eigentlich falsch ist.
Die Einheit der Geschwindigkeit ist aus zwei Einheiten zusammengesetzt, was daran liegt, dass die Geschwindigkeit aus zwei Größen zusammengesetzt ist.
Kilometer (km) ist die Einheit für die Strecke s, Stunden (h) ist die Einheit für die Zeit t. (Genauso können wir aber für die Strecke s die Einheit Meter (m) und für die Zeit t die Einheit Sekunden (s) wählen.)
Für die Geschwindigkeit werden also die Größen Strecke s und Zeit t miteinander verknüpft, und zwar so, dass die Strecke s durch die Zeit t geteilt wird. Man sagt z.B. die Geschwindigkeit beträgt 100 Kilometer pro Stunde oder 100 km/h.
Man erhält also die Geschwindigkeit, indem man die zurückgelegte Strecke s durch die dafür benötigte Zeit t dividiert. Das Ergebnis einer Division wird als Quotient bezeichnet.
Für die Geschwindigkeit gibt es wie für alle anderen physikalischen Größen ein Symbol, und zwar ein kleines “v” (aus dem Englischen: “velocity”).
Damit lässt sich die Geschwindigkeit folgendermaßen definieren:
Die Geschwindigkeit v gibt an, welche Strecke s ein Objekt in einer bestimmten Zeit t zurücklegt.
Man erhält sie aus dem Quotienten aus der Strecke s und der Zeit t:
Für gleichförmige Bewegungen gilt: 
Die Einheit der Geschwindigkeit lautet Meter pro Sekunde 
oder Kilometer pro Stunde 
Um die Geschwindigkeit zu bestimmen, müssen wir also die entsprechenden Strecken durch die benötigte Zeit teilen.
Da die Geschwindigkeit sich in unserem Beispiel nicht ändert – es handelt sich schließlich um eine gleichförmige Bewegung – reicht es aus, die gesamte zurückgelegte Strecke sges durch die gesamte dafür benötigte Zeit tges zu teilen.
Mit sges = 100 m und tges = 7,0 s ergibt sich
Da wir für die Strecke die Einheit Meter und für die Zeit die Einheit Sekunden gewählt haben, lautet die Einheit der Geschwindigkeit im Ergebnis “Meter pro Sekunde” (m/s).
Das Ergebnis wurde mit dem Taschenrechner berechnet und ist auf eine Nachkommastelle gerundet.
Wir können wir nun die Einheit m/s in die Einheit km/h umrechnen?
Dazu können wir uns folgende einfache Fragen stellen, die Du sicher alle selbst beantworten kannst und uns zum gewünschten Zusammenhang führen:
Wenn ein Objekt in einer Sekunde einen Meter zurücklegt, welche Strecke legt es dann in einer Minute zurück?
Richtig, 60 m, da eine Minute 60 Sekunden hat.
Welche Strecke legt es dann in einer Stunde zurück?
Da eine Stunde 60 Minuten hat, müssen wir wieder mit 60 multiplizieren, also (60 m x 60 =) 3.600 m.
Wie viele Kilometer sind 3.600 m?
“Kilo” steht für “1000”, 1 km entspricht also 1000 m. Damit gilt: 3.600 m = 3,6 km.
Ergebnis: In einer Stunde legt das Objekt also eine Strecke von 3,6 km zurück.
Damit beträgt die Geschwindigkeit 3,6 km/h. Das ist also das gleiche wie 1 m/s.
Bei der Umrechnung zwischen den Einheiten m/s und km/h haben wir also einen Faktor von 3,6. Den kann man sich leicht merken. Aber wie Du gesehen hast, sind die Überlegungen, die uns zu diesem Faktor geführt haben, ganz einfach.
Umrechnung zwischen den Einheiten m/s und km/h
Es gilt: 
Merke: Der Zahlenwert in km/h ist immer größer als der in m/s!
Mit der Definition der Geschwindigkeit für gleichförmige Bewegungen und der Umrechnung zwischen den beiden gebräuchlichen Einheiten, können wir nun einfache Aufgaben zur Berechnung der Geschwindigkeit lösen.
1. Ein Läufer läuft 400 m in 50 Sekunden.
Gegebene Größen: Strecke s = 400 m, Zeit t = 50 s
Zur Berechnung der Geschwindigkeit schreiben wir den bekannten Zusammenhang (die Formel zur Berechnung der Geschwindigkeit) auf und setzen dann die Werte ein:
Ergebnis: Die Geschwindigkeit des Läufers beträgt v = 8 m/s.
Wir können die Geschwindigkeit auch in km/h umrechnen. Dazu müssen wir den Zahlenwert mit dem Faktor 3,6 multiplizieren (s.o.) und erhalten die Geschwindigkeit v = 28,8 km/h.
2. Ein Auto fährt in 1 1/2 Stunden eine Strecke von 180 km.
Gegebene Größen: s = 180 km, t = 1,5 h
Es gilt: 
Ergebnis: Die Geschwindigkeit des Autos beträgt v = 120 km/h.
Wir können die Geschwindigkeit nun auch in m/s umrechnen, was zwar unüblich ist, für spätere Rechnungen aber erforderlich sein könnte. Dazu müssen wir den Zahlenwert durch den Faktor 3,6 dividieren (s.o.) und erhalten die Geschwindigkeit v = 33,3 m/s.
Bei allen Rechnungen kommt es nicht nur auf das Ergebnis an sondern auch auf die korrekte Darstellung der Rechnung. Dazu gehört die Formelschreibweise und das Mitschreiben der Einheiten:
Formeln, die Divisionen enthalten, werden immer als Bruch geschrieben:
Beispiel:
Ein Divisionszeichen “:” hat in einer physikalischen Berechnung nichts verloren!
Zu jedem Zahlenwert gehört eine Einheit! Schreibe die Einheiten in jeder Formel und beim Ergebnis stets mit! Ergebnisse ohne Einheit sind falsch!
Beispiel: 
Die korrekte Einheit beim Ergebnis ergibt sich aus den Einheiten, die Du in der Rechnung eingesetzt hast. In diesem Beispiel kommt die Einheit m/s heraus, weil die Strecke in m, die Zeit in s eingesetzt wurde.
Die Geschwindigkeit lässt sich auch aus dem Zeit-Weg-Diagramm ermitteln. Der Quotient 
entspricht nämlich genau der Steigung im t-s-Diagramm.
Um die Steigung einer Gerade zu ermitteln, kennst Du sicher die Möglichkeit, ein Steigungsdreieck zu zeichnen. Dazu wählst Du zwei Punkte auf der Geraden aus, am besten dort, wo sie gut ablesbar sind.
Wollen wir die Steigung im t-s-Diagramm ermitteln, so müssen wir zwei Punkte (t1 /s1) und (t2 / s2) vom Grafen auswählen, der ja für eine gleichförmige Bewegung ebenfalls eine Gerade ist. Bei einer Geraden macht es keinen Unterschied, welche Punkte man wählt – Du kannst also zwei beliebige Punkte auf der Geraden auswählen. Meist bietet es sich an, als ersten Punkt den Ursprung zu wählen.
Beachte dabei:
Je größer das Steigungsdreieck ist, umso weniger wirken sich kleine Ungenauigkeiten beim Ablesen aus. Daher sollte das Steigungsdreieck möglichst groß sein:
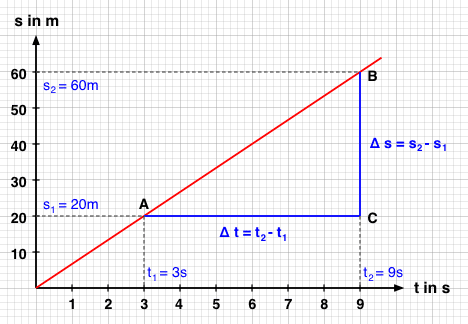
Wir haben uns in diesem Beispiel für die beiden Punkte A (3s | 20m) und B (9s | 60m) entschieden. Um nun das Steigungsdreieck zu zeichnen, zeichnen wir vom ersten Punkt aus eine waagerechte Linie (Parallele zur t-Achse) nach rechts und vom zweiten Punkt ausgehend eine senkrechte Linie (Parallele zur s-Achse) nach unten. Der Schnittpunkt der beiden Linien ist der Punkt C des Steigungsdreiecks.
Um nun die Steigung zu berechnen, zählst Du, um wie viele Zeiteinheiten Du vom Ursprung aus nach rechts gegangen bist (das entspricht dem Zeitintervall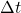 
) und wie viele Streckeinheiten Du nach unten gegangen bist (dies entspricht dem Streckenintervall 
).
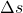Die Formel zur Berechnung der Steigung aus dem Steigungsdreieck lautet nun:
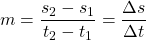
Wir teilen also den zurückgelegten Weg 
durch die dafür benötigte Zeit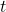 
. Das entspricht gerade der Definition für die Geschwindigkeit 
.
Es gilt also:
Die Steigung im t-s-Diagramm entspricht der Geschwindigkeit.
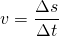
Die Berechnung der Geschwindigkeit mit Hilfe des Steigungsdreiecks ergibt:
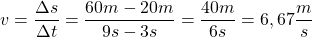
Wichtig dabei ist, auch hier die Einheiten für die Größen s (hier: m) und t (hier: s) mitzuschreiben. Als Einheit ergibt sich natürlich die Einheit der Geschwindigkeit, hier m/s.
Da man die Steigung in einem Zeit-Weg-Diagramm auf einen Blick erfassen kann, lässt sich auch eine Änderung der Geschwindigkeit aus der Änderung der Steigung erkennen, oder es lassen sich zwei verschiedene Geschwindigkeiten vergleichen.
Stellt man zwei verschiedene gleichförmige Bewegungen in einem t-s-Diagramm dar, so lässt sich sofort erkennen, welche Geschwindigkeit größer ist:
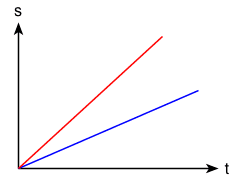Die rote Gerade ist steiler, also ist die Geschwindigkeit größer.
Je steiler der Graf, desto größer die Geschwindigkeit.
Bewegt sich ein Objekt nicht gleichförmig, sondern mal schneller und mal langsamer – wie z.B. ein Auto im Stadtverkehr – so müssen wir zwischen Momentan- und Durchschnittsgeschwindigkeit unterscheiden. Im Auto können wir auf dem Tachometer die Geschwindigkeit ablesen. Dies ist die Momentangeschwindigkeit. Steht der Zeiger vom Tachometer still, so bleibt die Geschwindigkeit konstant. Bewegt sich der Zeiger jedoch, so ändert sich die Geschwindigkeit.
Wenn wir die Geschwindigkeit einer gesamten Autofahrt mit der Formel berechnen wollen, so erhalten wir stets die Durchschnittsgeschwindigkeit (auch mittlere Geschwindigkeit genannt).
Beispiel:
Ein Auto fährt von Bremen nach Hamburg. Die Strecke beträgt 120 km, ein Autofahrer benötigt 1:30 Stunden.
Die Berechnung der Durchschnittsgeschwindigkeit ergibt: 
Ein Fahrzeug, welches sich gleichförmig bewegt, müsste die ganze Zeit genau mit dieser Geschwindigkeit fahren, um den Weg in der gleichen Zeit zurückzulegen.
In der Realität wird das Auto auf dem Weg jedoch mal deutlich langsamer und mal deutlich schneller gefahren sein.
