Kapazität eines Kondensators

Kondensator als Ladungs- und Energiespeicher

Ein Kondensator ist ein Bauelement zur Speicherung elektrischer Ladung bzw. elektrischer Energie. Die Kapazität eines Kondensators beschreibt die Aufnahme- bzw. Speicherfähigkeit und soll zunächst genauer erläutert werden.

Fragen:

• Welche Ladungsmenge befindet sich bei einer bestimmten Spannung auf den Platten?
• Wie viel Energie kann ein Kondensator speichern?

Damit ein Kondensator möglichst viel elektrische Energie speichern kann, muss die Ladungsmenge auf jeder Platte möglichst groß sein. Die gespeicherte Ladungsmenge eines Kondensators hängt u.a. von der angelegten Spannung ab.

Es gilt:

Je desto größer die Spannung, umso größer die gespeicherte Ladungsmenge auf den Platten.

Experimentell ergibt sich, dass die Ladungsmenge auf den Platten zur angelegtern Spannung proportional ist:

       bzw.        

Diese Konstante gibt an, welche Ladungsmenge bei einer bestimmten Spannung gespeichert werden kann.

Die Speicherfähigkeit eines Kondensators für elektrische Ladung wird durch die physikalische Größe Kapazität C angegeben.

Wovon hängt die Kapazität eines Kondensators ab?

Die Kapazität eines Kondensator hängt also nicht von der angelegten Spannung ab. Welche Ladungsmenge eine Kondensator bei einer bestimmten Spannung aufnimmt, wird allein durch die Bauform bestimmt.

Fragen:

• Von welchen Größen hängt die Kapazität eines Kondensators ab?
• Wie kann man einen Kondensator mit einer möglichst großen Kapazität bauen?

Um diese Frage zu klären, werden folgende Versuche durchgeführt:

Versuch 1:  Zusammenhang zwischen Plattenabstand und angelegter Spannung

Der Kondensator wird geladen und anschließend von der Spannungsquelle getrennt. (Dieser Versuch wurde bereits im Abschnitt “Versuche mit dem Plattenkondensator” beschrieben). Anschließend wird der Plattenabstand verändert.

Beobachtung:

Wird der Plattenabstand größer, vergrößert sich die Spannung.

Hinweis: Da die Spannungsquelle vom Kondensator getrennt wurde, können keine Ladungen zu- oder abfließen. Die Ladungsmenge muss also konstant geblieben sein.

Ergebnis:

Aus der Definition der Kapazität 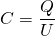ergibt sich:

Je größer die Spannung, umso kleiner die Kapazität

und damit:

Je kleiner der Plattenabstand, umso größer die Kapazität

Versuche zeigen: Halbiert man den Plattenabstand (bei konstanter Spannung), verdoppelt sich die Ladungsmenge auf den Platten und damit die Kapazität:

Für die Kapazität eines Kondensators gilt (für U = konst.):

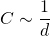        (1)

Versuch 2:  Zusammenhang zwischen Plattenfläche und Ladungsmenge

Mit einer kleinen Testplatte werden Ladungen von einer Kondensatorfläche abgenommen (Die Ladungen sitzen außen, da sie von den entgegengesetzten Ladungen der anderen Platte angezogen werden).

Berührt man anschließend mit der Testplatte ein Elektroskop, so ist der Zeigerausschlag umso größer, je mehr Ladungen auf der Platte sind (und damit je höher die Spannung war).

Wiederholt man den Versuch mit einer größeren Testplatte (oder mit zwei gleichen Testplatten), wird der Zeigerausschlag am Elektroskop größer.

Ergebnis:

Je größer die Fläche A einer Platte ist, umso größer ist die Ladungsmenge auf der Platte (bei gleicher Spannung).

Aus der Definition der Kapazität 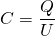ergibt sich damit:

Je größer die Fläche A der Platte, desto größer die Kapazität

Versuche zeigen: Verdoppelt man die Plattenfläche bei gleicher Spannung, verdoppelt sich auch die Ladung auf einer Platte.

Es gilt also außerdem:

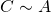        (2)

Aus den Proportionalitäten (1) und (2) ergibt sich:

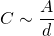
und damit

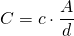
Das gilt streng genommen nur für sehr große Kondensatorplatten, denn Voraussetzung dafür ist eine vollständige Homogenität des Feldes.

Den Proportionalitätsfaktor nennt man elektrische Feldkonstante ε₀.

Diese Konstante lässt sich experimentell ermitteln, indem man die Ladungsmenge bei bestimmten Spannungen für unterschiedliche Flächen und Abstände misst.

Der Literaturwert der elektrischen Feldkonstante beträgt:

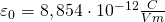
Damit lässt sich die Kapazität eines Kondensators aus seinen Abmessungen berechnen:

Hinweis: Dabei ist A die Fläche einer Kondensatorplatte, da in der Formel die Ladungsmenge einer Platte eingesetzt wurde.

Berechnung der Kapazität des Plattenkondensators aus den Versuchen:

Nun lässt sich die Kapazität des Plattenkondensators aus den Versuchen berechnen. Dazu wird die Fläche der Kondensatorplatten bestimmt. Da diese rund sind, gilt: .

Der Radius der Platten beträgt r = 30cm, damit ergibt sich die Fläche zu

.

Wird der Abstand auf d = 2mm (=0,002m) eingestellt, beträgt die Kapazität:

Da dies nur etwas mehr als ein Milliardstel Farad ist, scheint ein Farad also eine sehr große Kapazität zu sein!

Frage:

Welche Fläche müssten die Platten eines Plattenkondensators bei einem Plattenabstand von 1mm haben, damit die Kapazität des Kondensators 1Farad beträgt?

Berechnung:

Dazu stellt man die Formel nach A um und setzt für den Abstand d = 1mm = 0,001m ein:

nach A umgestellt lautet die Gleichung:

Nun werden die Werte eingesetzt:

Damit beträgt die notwendige Fläche

Es ist offensichtlich, dass eine so große Fläche bei einem Kondensator nicht realisierbar ist – zumal Kondensatoren meist sehr klein und kompakt sind (nur einige Millimeter groß) – auf jeder Platine (z.B. im Computer) befinden sich viele Kondensatoren, deren Kapzitäten in der Größenordnung von einigen μC oder nC liegen.

Tatsächlich gibt es aber relativ kompakte Kondensatoren mit Kapazitäten in der Größenordnung von einem Farad und sogar darüber. Es muss also andere Möglichkeiten geben, dies zu realisieren.

Diese sind:

• Die Kondensatorplatten bestehen aus dünnen Folien, die aufgerollt werden und so bei einer großen Fläche nur wenig Platz brauchen.
• Die Betriebsspannungen liegen meist deutlich unterhalb der Spannungen, die wir im Schulversuch verwendet haben – so lässt sich der Abstand der Platten reduzieren, was die Kapazität bei gleicher Fläche erhöht.

Eine weitere Möglichkeit, die Kapazität um ein Vielfaches zu erhöhen liegt darin, den Raum zwischen den Kondensatorplatten mit einem Nichtleiter (Dielektrikum) auszufüllen.

Lies dazu den folgenden Abschnitt!